
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Тема 7. Выборочный метод в статистических исследованиях
Понятие о выборочном методе. Выборочное наблюдение – это такое несплошное наблюдение, при котором отбор подлежащих исследованию единиц совокупности осуществляется случайно, отобранная часть подвергается исследованию, после чего результаты распространяются на всю совокупность.
К использованию выборочного метода прибегают в следующих случаях: когда само наблюдение связано с порчей или уничтожением наблюдаемых единиц (например, пряжа на крепость, электрическая лампочка на продукт горения); большой объем совокупности; значительные затраты (финансовые и трудовые).
Обычно выборочному обследованию подвергается 5–10% всей совокупности, реже 15–25%.
Целью выборочного наблюдения является определение характеристик генеральной средней 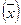 и генеральной доли (р).
и генеральной доли (р).
Характеристиками выборочной совокупности являются – средняя величина изучаемого признака  и доля определенных исследуемых единиц (w), которые отличаются от генеральных характеристик на величину предельной ошибки выборки для средней величины (
и доля определенных исследуемых единиц (w), которые отличаются от генеральных характеристик на величину предельной ошибки выборки для средней величины (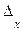 ) и для доли (
) и для доли (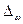 ). Поэтому необходимо вычислять ошибку выборки или ошибку репрезентативности, которая определяется по формулам, разработанным в теории вероятности для каждого вида выборки и способа отбора.
). Поэтому необходимо вычислять ошибку выборки или ошибку репрезентативности, которая определяется по формулам, разработанным в теории вероятности для каждого вида выборки и способа отбора.
Существуют следующие способы отбора единиц в выборочную совокупность:
- повторный отбор по схеме возвращенного шара, обычно называемый повторной выборкой.
При повторном отборе вероятность попадания каждой отдельной единицы в выборку остается постоянной, т.к. после отбора какой–то единицы, она снова возвращается в совокупность и снова может быть выбранной.
- бесповторный отбор по схеме невозвращенного шара, называемый бесповторной выборкой. В этом случае каждая отобранная единица не возвращается обратно, и вероятность попадания отдельных единиц в выборку все время изменяется (для оставшихся единиц она возрастет). Примером может служить жеребьевка, таблицы случайных чисел.
Выборочные показатели, как правило, не совпадают с соответствующими показателями генеральной совокупности, а несколько отличаются от них в одну или другую сторону, т.е. при выборочном методе всегда могут возникнуть ошибки, которые можно подразделить на ошибки регистрации и ошибки репрезентативности.
Ошибки регистрации, присущие сплошному и выборочному наблюдению. Причина этих ошибок может быть разная: и по вине того, кто проводит наблюдение, и по вине отвечающего на вопросы, и от способа наблюдения. Ошибки данного вида можно уменьшить, если тщательно провести подготовку кадров и продумать организацию проведения наблюдения.
Ошибки репрезентативности имеют место только в выборочном наблюдении, они могут быть как случайными, так и систематическими, которые возникают в результате нарушения случайности отбора. Случайная ошибка возникает в силу того, что исследуется часть, а не вся совокупность.
Главная задача выборочного метода состоит в определении величины случайных ошибок репрезентативности. Их нахождение позволяет судить о точности выборки, о возможности распространения выборочных характеристик на генеральную совокупность.
Ошибка выборки для средней величины будет равна 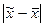 , а для доли
, а для доли 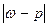 . Однако эту разницу определить невозможно, так как
. Однако эту разницу определить невозможно, так как 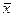 и
и 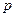 неизвестны и для их определения и проводится выборочное наблюдение.
неизвестны и для их определения и проводится выборочное наблюдение.
Случайные ошибки выборки определяются по формулам, разработанным на основе теории вероятности, и носят вероятностный характер.
В практике выборочных обследований наибольшее распространение получили следующие выборки: собственно–случайная; механическая; типическая; серийная; комбинированная.
Для каждого вида выборок существует своя методика определения ошибок, рассмотрим каждую из них.
Ошибки собственно-случайной выборки. Собственно – случайная выборка – это такая, при которой отбор единиц в выборочную совокупность производится непосредственно из всей массы единиц генеральной совокупности.
При этом количество отобранных единиц обычно определяется исходя из принятой доли выборки.
Доля выборки  есть отношение числа единиц выборочной совокупности (n) к численности единиц генеральной совокупности (N).
есть отношение числа единиц выборочной совокупности (n) к численности единиц генеральной совокупности (N).
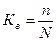 . .
| (7.1) |
Так при 5% выборке из партии товара в 2000 единиц численность выборки (n) составит 100 единиц ( ), а при 20% выборке она составит 400 единиц (
), а при 20% выборке она составит 400 единиц (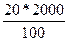 ).
).
Важное условие собственно случайной выборки состоит в том, что каждой единице генеральной совокупности предоставляется равная возможность попасть в выборочную совокупность.
При определении точности выборочных показателей различают среднюю ошибку и предельную.
Средняя ошибка выборки (μ) представляет среднее квадратическое отклонение возможных значений выборочной средней от генеральной средней.
Среднюю ошибку выборки находят по формуле
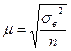 . .
| (7.2) |
где 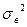 – дисперсия в выборочной совокупности.
– дисперсия в выборочной совокупности.
В каждой конкретной выборке расхождение между выборочной средней  и генеральной средней
и генеральной средней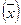 , может быть меньше или равно ей или больше μ.
, может быть меньше или равно ей или больше μ.
Причем каждое из этих расхождений имеет различную вероятность. Предельную ошибку выборку можно рассчитать по следующей формуле.

| (7.3) |
где μ – средняя ошибка выборки;
t – коэффициент доверия, который определяется по таблице значений интегральной функции Лапласа при заданной вероятности P.
Коэффициент доверия t приводится в специальных математических таблицах. Например, при вероятности Р(t) = 0,683 t = 1, если Р(t) = 0,954, то t = 2, при Р(t) = 0,997 коэффициент доверия равен 0,997.
Эти показатели означают, что с вероятностью, равной 0,683 можно утверждать, что предельная ошибка выборки не превысит μ; с вероятностью 0,954 можно утверждать, что предельная ошибка D (расхождение между выборочной и генеральной средней) не превзойдет двукратную среднюю ошибку, т.е. 2 μ; при вероятности 0,997, можно утвержать, что предельная ошибка не превзойдет 3 μ.
Так как предельная ошибка выборки связана со средней ошибкой и коэффициентом доверия, то ее расчет производится в следующем порядке: 1) по выборочным данным определяется средняя ошибка выборки, т.е. μ; 2) задается вероятность (Р), с которой искомая предельная ошибка гарантируется (так называемая доверительная вероятность); 3) в соответствии с доверительной вероятностью по таблицам определяется τ; 4) средняя ошибка выборки умножается на t, т.е. находится  =
= 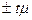 .
.
Приведенные выше формулы ошибок выборки рассматривались для оценки по выборочным данным генеральной средней. Рассмотренные формулы применимы и для определения ошибок выборки при установлении доли тех или иных единиц в совокупности. При этом следует лишь вместо дисперсии 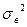 пользоваться показателем дисперсии альтернативного признака, которая равна произведению доли единиц, обладающих данным признаком (p), на долю единиц, не обладающих данным признаком (1 – p =q), т.е. равна pq.
пользоваться показателем дисперсии альтернативного признака, которая равна произведению доли единиц, обладающих данным признаком (p), на долю единиц, не обладающих данным признаком (1 – p =q), т.е. равна pq.
Тогда теоретическая формула средней ошибки для доли запишется как
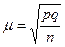 , ,
| (7.4) |
а предельная ошибка выборки выразится как
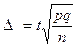 . .
| (7.5) |
Поскольку генеральная доля (p) неизвестна (ради ее определения и проводится выборочное обследование), то для практических целей используются расчетные формулы, в которых вместо генеральной доли (p) принимается выборочная частость (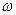 ).
).
Таким образом, формула средней ошибки для доли будет
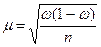 . .
| (7.6) |
И соответственно предельная ошибка для доли будет исчисляться по формуле
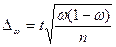 . .
| (7.7) |
Все приведенные выше формулы для нахождения ошибок выборки приводились применительно к повторному отбору. Однако на практике чаще применяется бесповторный отбор, гарантирующий более точные результаты (большую репрезентативность), поскольку при этом отборе исключается возможность повторного обследования одних и тех же единиц, генеральной совокупности. При бесповторном отборе предельная ошибка выборки для средней величины определяется по формуле
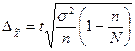 , ,
| (7.8) |
а для доли
 . .
| (7.9) |
Так как множитель под корнем  всегда меньше единицы, то предельная ошибка выборка, рассчитываемая по формулам бесповторного отбора, будет меньше, чем при расчете по формулам повторного отбора, что и подтверждает большую репрезентативность бесповторного отбора.
всегда меньше единицы, то предельная ошибка выборка, рассчитываемая по формулам бесповторного отбора, будет меньше, чем при расчете по формулам повторного отбора, что и подтверждает большую репрезентативность бесповторного отбора.
Использование формул предельной ошибки выборки. На основе формул предельной ошибки выборки могут решаться следующие задачи:
- определение доверительных пределов генеральной средней (или доли) с заданной вероятностью;
- определение вероятности того, что расхождение между выборочными и генеральными характеристиками не превзойдет определенную заданную величину;
- определение необходимой численности (объема) выборки, которая с определенной вероятностью обеспечит заданную точность выборочных показателей.
Определение необходимой численности выборки. В практике выборочного наблюдения возникает потребность нахождении численности (объема) выборки, которая с определенной вероятностью обеспечит заданную точность результатов наблюдения. Формулы для определения необходимой численности выборки (n) легко получить непосредственно из формул ошибок выборки.
При собственно–случайном повторном отборе численность выборки определяется по формуле
 , (для средней) , (для средней)
| (7.10) |
если вместо 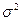 подставить pq – дисперсию альтернативного признака, то
подставить pq – дисперсию альтернативного признака, то
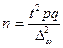 , (для доли) , (для доли)
| (7.11) |
Аналогично из формулы предельной ошибки выборки для бесповторного отбора
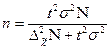 , (для средней) , (для средней)
| (7.12) | |
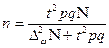 (для доли) (для доли)
| (7.13) | |
Дисперсию альтернативного признака (pq), если ничего неизвестно о доле (р), можно принять максимальной pq = 0,25, получаемое при предположении равенства p и q, т.е. если p=q=0,5.
Ошибки механической выборки. Это разновидность собственно – случайной. В этом случае вся генеральная совокупность делится на n равных частей и затем из каждой части отбирается одна единица.
Все единицы генеральной совокупности должны располагаться в определенном порядке. При этом по отношению к изучаемому показателю единицы генеральной совокупности могут быть упорядочены по существенному, второстепенному или нейтральному признаку. При этом из каждой группы должна отбираться та единица, которая находится в середине каждой группы. Это позволяет избежать систематической ошибки выборки.
Данный вид выборки применяют при обследовании покупателей в магазинах, посетителей в поликлиниках, например обследуется каждый 5 или 100 –ая единица.
Формулы для расчета средней и предельной ошибок выборки такие же как и для собственно–случайной выборки.
Ошибки выборки при типической выборке. При типической выборке отбор единиц осуществляется не непосредственно из всей массы единиц генеральной совокупности, а из отдельных ее частей, выделенных по определенному существенному признаку, то есть генеральная совокупность разделяется на однородные типические группы. Затем из каждой типической группы собственно–случайной или механической выборкой производится индивидуальный отбор единиц в выборочную совокупность. Следовательно, ошибка выборки при этом методе отбора будет зависеть не от вариации признака во всей совокупности, а от вариации признака внутри каждой группы, а эта внутригрупповая вариация измеряется средней из групповых дисперсий.
При типической выборке в формулах ошибок выборки вместо общей дисперсии 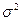 следует учитывать среднюю из групповых (
следует учитывать среднюю из групповых (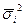 ), если речь идет о средней, и
), если речь идет о средней, и  , если речь идет о доле.
, если речь идет о доле.
Таким образом, формулы предельной ошибки выборки при типическом отборе представлены в табл.7.1. Поскольку, исходя из правила сложения дисперсий, средняя из групповых дисперсий всегда меньше общей дисперсии, то, очевидно, что при типическом отборе ошибка выборки будет меньше.
Записанные выше формулы, применимы при пропорциональном отборе, т.е. когда из каждой выделенной группы отбирается одинаковый процент единиц.
Таблица 7.1
Формулы для расчета предельной ошибки выборки при типическом отборе
| Показатель | Для повторного отбора | Для бесповторного отбора |
| Для средней | 
| 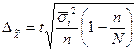
|
| Для доли | 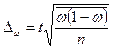
| 
|
Объем выборки из типической группы при отборе пропорциональном численности типических групп, определяется по формуле
 , ,
| (7.14) |
где 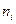 – объем выборки из типической группы;
– объем выборки из типической группы;
 – объем типической группы.
– объем типической группы.
Для определения необходимой численности выборки при типическом отборе сначала определяется общая численность  по формуле
по формуле
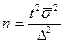 (для повторного отбора) (для повторного отбора)
| (7.15) |
и
 (для бесповторного отбора) (для бесповторного отбора)
| (7.16) |
а затем уже определяется необходимый отбор из каждой группы в зависимости от вида отбора: пропорционального, непропорционального, оптимального, учитывающего и численность единиц в каждой группе, и вариацию признака.
Ошибки выборки при серийном отборе. При серийной выборке совокупность делят на одинаковые по объему группы – серии. В выборочную совокупность отбираются серии. Внутри серий производится сплошное наблюдение единиц, попавших в серию. Ошибка выборки будет зависеть не от вариации признака во всей совокупности, а от вариации серийных средних, которая измеряется межсерийной дисперсией.
Если общее число серий в генеральной совокупности обозначить через R, а число отобранных – через r, то формулы предельной ошибки выборки при серийном отборе можно записать следующим образом:
Для повторного отбора
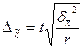 (для средней) (для средней)
| (7.17) |
где  – межсерийная дисперсия, которая рассчитывается по формуле
– межсерийная дисперсия, которая рассчитывается по формуле
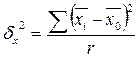
| (7.18) |
где  выборочная средняя серии,
выборочная средняя серии, 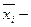 выборочная средняя серийной выборки, r– число отобранных серий.
выборочная средняя серийной выборки, r– число отобранных серий.
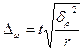 (для доли) (для доли)
| (7.19) |
Для бесповторного отбора
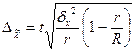 (для средней) (для средней)
| (7.20) |
R– число серий генеральной совокупности
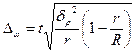 (для доли) (для доли)
| (7.21) |
Комбинированная выборка. В статистической практике выборочное наблюдение из больших массивов генеральной совокупности часто проводится в виде комбинированной, или ступенчатой, выборки. При комбинированной выборке выборочная совокупность единиц формируется в результате так называемого ступенчатого отбора. Например, для обследования успеваемости студентов факультета выборочную совокупность можно сформировать в результате двухступенчатого отбора: вначале провести случайный отбор групп (как серий), а затем в каждой группе методом механической или собственно-случайной выборки отобрать определенное число студентов.
Распространение результатов выборки на генеральную совокупность. Конечной целью выборки является распространение выборочных данных на генеральную совокупность. Если исследователя интересуют средние показатели или доля, то в таком случае, как было указано выше, к выборочной средней или частости прибавляется предельная ошибка выборки и определяются доверительные интервалы средней (или доли) относительно генеральной совокупности.
Эти интервалы служат основой для оценки абсолютных, итоговых величин генеральной совокупности. В таких случаях для распространения выборочных данных необходимо обязательно знать численность единиц генеральной совокупности.
Есть два способа распространения выборочных данных на генеральную совокупность: способ прямого пересчета и способ поправочных коэффициентов.
При первом способе среднее значение признака выборочной совокупности умножается на число единиц в генеральной совокупности.
Второй способ применяется в более сложных случаях, например при обследовании совокупности по ряду признаков, отличающихся своей репрезентативностью, а также когда выборочное наблюдение проводится с целью уточнения результатов сплошного наблюдения.
|
Дата добавления: 2014-01-06; Просмотров: 581; Нарушение авторских прав?; Мы поможем в написании вашей работы!