Индексы плоских сеток

Установка кристаллов

Выбор кристаллографических осей и единичной грани называется установкой кристалла.

От установки кристалла целиком зависят символы всех его граней. Поэтому выбор координатных осей и единичной грани должен быть подчинён определённым правилам с тем, чтобы установка кристалла была однозначной для каждого вещества.

Элементарной ячейкой называется наименьший параллелепипед повторяемости, обладающий сингонией данной решётки при максимальном числе равных углов между его рёбрами.

Каждая сингония характеризуется своей формой элементарной ячейки.

Элементарные ячейки разных веществ, кристаллизующихся в одной сингонии, отличаются линейными размерами своих рёбер. Кристаллографические оси должны обязательно совпадать с направлениями рёбер элементарной ячейки, а единичная грань должна отсекать отрезки, пропорциональные длинам соответственных рёбер ячейки.

Таким образом, если установка кристалла сделана правильно, то углы между кристаллографическими осями будут равны углам между рёбрами.

Положение плоских сеток относительно избранной системы координат численно характеризуют, как и положение граней кристалла, с помощью индексов. Индексы плоских сеток могут быть и целыми и дробными.

Три параметра (р, q и r) данной плоской сетки, измеренные промежутками координатных рядов, вполне определяют положение сетки в кристалле.

Числа обратные числовым параметрам p,q,r плоской сетки, называются её индексами.

Совокупность индексов данной плоской сетки, взятая в круглые скобки, называется символом этой сетки.

Отношение индексов плоских сеток одной и той же серии постоянно и, как отношение рациональных чисел, всегда может быть представлено в виде отношения взаимно простых целых чисел. Эти числа называются индексами серии. Совокупность индексов серии, взятых без каких-либо знаков между ними в круглые скобки, называется символом серии или сериальным символом.

Так как индексы плоской сетки обратны её параметрам, то чем больше численные значения индексов символа сетки данной серии, тем ближе к началу координат расположена эта сетка. Плоская сетка, символ которой тождественен с сериальным символом, является среди всех плоских сеток данной серии или ближайшей к началу координат, или второй от него.

5. СИМЕТРИЯ ПРОСТРАНСТВЕННЫХ РЕШЁТОК

В кристаллах возможны только такие элементы симметрии, которые не противоречат свойствам пространственной решётки. Однако симметрия кристалла не тождественна симметрии его решётки, т.к. кристаллический многогранник конечная фигура, а пространственная решётка геометрический образ бесконечного протяжения.

Осью трансляции называется такое направление в бесконечной фигуре, при трансляции вдоль которого на некоторое определённое растояние фигура совмещается сама с собой.

Наименьшее растояние при перемещении на которое вдоль оси трансляции фигура самосовмещается, называется периодом трансляции.

Элементарными трансляциями в пространственной решётке являются промежутки рядов решётки.

Благодаря трансляции в пространственной решётке появляются новые элементы симметрии плоскость скользящего отражения и винтовые оси.

Плоскостью скользящего отражения называется плоскость, при отражении в которой и последующей трансляции вдоль неё на определённое расстояние фигура совмещается сама с собой.

Винтовой осью симметрии называется прямая линия, при повороте вокруг которой и последующей трансляции вдоль неё фигура совмещается со своим исходным положением в пространстве. Винтовые оси бывают 1-го, 2-го, 3-го, 4-го и 6-го порядка.

Отметим следующие особенности симметрии пространственных решёток.

1. Ряд решётки, параллельный оси симметрии, является осью симметрии.

2. Плоская сетка решётки, параллельная плоскости симметрии есть плоскость симметрии той же решётки.

3. Пространственная решётка всегда имеет бесконечно большое число центров инверсии, совпадающих с центрами элементарных ячеек.

4. В пространственных решётках всегда есть трансляции, параллельные и перпендикулярные осям и плоскостям симметрии.

5. Если в решётке есть ось симметрии n-го порядка, то в той же решётке имеются и n осей второго порядка, перпендикулярных к оси L_n.

Трансляционные решётки

Решётки, в которых промежуток любого ряда может рассматриваться как элементарная трансляция, называются трансляционными.

Различают четыре типа трансляционных решёток.

1. Решётки, элементарная ячейка которых является примитивным параллелепипедом и имеет узлы только в своих вершинах, называются примитивными.

2. Решётки, элементарная ячейка которых кроме узлов в вершинах имеет ещё один узел в центре объёма, называются объёмно-центрированными.

3. Решётки, элементарная ячейка которых имеет узлы в вершинах и центрах всех граней, называются гранецентрированными.

Рис. 5.1. Двумя трансляциями можно вывести все узлы плоской сетки

4. Решётки, элементарная ячейка которых имеет узлы не только в вершинах, но и в центрах двух параллельных граней называются базоцентрированными.

Распределение трансляционных решеток по сингониям показано в таблице 2 на рис. 5.1. Всего во всех семи сингониях получаем 14 различных трансляционных решеток. Впервые все виды трансляционных решеток были выведены Бравэ, поэтому их часто называют также решетками Бравэ.

Е. С. Федоров, разрабатывая свою теорию кристаллического строения, пришел к выводу, что любая из решеток Бравэ может быть получена с помощью однородных деформаций (растяжения, сжатия или сдвига) из четырех идеальных решеток, из которых три являются решетками кубической сингонии. В зависимости от того, из какой исходной предельной решетки путем минимальных деформаций получена решетка Бравэ, она относится к кубическому или к гексагональному типу. Таким образом, по Федорову весь мир кристаллов подразделяется на два типа - кубический и гексагональный. В этом заключается сущность одного из основных законов кристаллографии - закона кристаллографических пределов Федорова. В соответствии с этим законом кристаллы кубической и гексагональной сингонии являются ”идеальными” или “предельными”, а кристаллы остальных сингоний есть производные от идеальных.

Поскольку на кристаллических кристаллах преобладают грани, отвечающие плоским сеткам с наибольшей ретикулярной плотностью, четырем основным типам решеток должны быть свойственны различные преобладающие грани. Так, например, самые плотные плоские сетки в простой решетке имеют символ (100), в объемноцентрированной - (110), а в гранецентрированной - (111). На кристаллах с этими типами решеток указанными символами обладают, как правило, и наиболее часто встречающиеся грани.

Отсюда вытекает возможность по внешним признакам и форме кристалла определять их тип решетки. Зная тип решетки и углы между гранями можно определить состав вещества. Такой метод определения вещества, разработанный Федоровым и известный под названием кристаллохимического анализа, имеет следующие преимущества:

1) Ничтожность количества вещества при диагнозе,

2) Неуничтожаемость вещества при диагнозе, чего нельзя избежать при химическом анализе,

3) Сравнительная быстрота определения.

Кристаллохимический анализ Федорова оказал большое влияние на развитие нового отдела кристаллографии - кристаллохимии.

Как указывалось выше, на элементарную ячейку примитивной решетки всегда приходится только один узел, т. к. каждый узел примитивной решетки принадлежит восьми соседним параллелепипедам повторяемости. На долю объемноцентрированной решетки приходится уже два узла, ибо узел, находящийся в центре решетки (ячейки), целиком принадлежит ей. Элементарной ячейке базоцентрированной решетки принадлежат также два узла (по 1/8 узла от каждой вершины и по 1/2 узла от двух граней ячейки). Наконец, в гранецентрированной решетке каждой ячейке принадлежат 4 узла (один узел - от всех вершин ячейки и три узла - от всех шести её граней).

Объемно-, гране- и базоцентрированные решетки можно рассматривать как совокупность нескольких простых решеток с одинаковыми элементарными ячейками, выдвинутых одна в другую. Число этих простых решеток равно количеству узлов, приходящихся на ячейку непримитивной решетки. Например, гранецентрированную решетку можно представить себе состоящей из четырех одинаковых параллельно расположенных примитивных решеток.

Не примитивную, т. е. сложную, элементарную ячейку характеризуют координатами принадлежащих ей узлов. Совокупность координат узлов, входящих в элементарную ячейку, называют базисом ячейки.

Координаты узла, измеренные промежутками рядов, принятых за кристаллографические оси, называют индексами узла. Совокупность индексов узла, взятая в двойные квадратные скобки, образует символ узла.

Если x, y и z - координаты некоторого узла, то индексами узла будут u=x/a₀, v=y/b₀ и w=z/c₀, где a₀, b₀ и c₀ - промежутки координатных рядов. Символ данного узла, следовательно, [[uvw]].

Таким образом, базис решетки должен состоять из символов тех узлов, которые принадлежат элементарной ячейке. В соответствии с этим, например, в базис объемноцентрированной ячейки должны войти символы двух узлов, а в базис гранецентрированной ячейки - символы четырех узлов.

На рис. 5.2 приведены элементарные ячейки всех четырех типов трансляционных решеток и базисы этих ячеек. Узлы, символы которых входят в базис ячейки, обозначены на чертеже более крупными точками.

	Рис. 5.2. Базисы элементарных ячеек четырех типов трансляционных решеток

		[[000]] [[­^1/2­^1/2­0]] [[^1/2^1/2]] [[0^1/2^1/2]]
		[[000]]   [[­^1/2­^1/2­0]]		[[000]]   [[­^1/2­^1/2^1/2­]]
	[[000]]
		Рис. 5.2. Базисы элементарных ячеек четырех типов трансляционных решеток

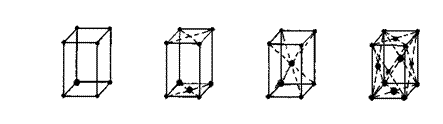
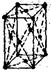
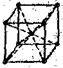
Таблица 5.1 – Ячейки трансляционных решёток

Сингония	Трансляционная решётка
Примитивная	Базецентрированная	Объёмноцентрированная	Гранецентрированная
Триклинная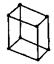
Моноклинная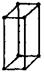
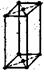
Ромбическая
Тригональная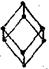
Тетрагональная
Гексагональная
Кубическая

ЧАСТЬ ВТОРАЯ

Дата добавления: 2014-01-06