Математические предложения

Лекция 6. Высказывания и высказывательные формы (Математические предложения)

Основные выводы

Способы определения понятий

Рассмотрим виды определений.

1. При изучении математики в начальных классах определения через род и видовое отличие используется не всегда. Но понятий в начальном курсе математики изучается много. Как же их определяют?

2. Неявные определения: контекстуальные и остенсивные.

В контекстуальных определениях содержание нового понятия раскрывается через отрывок текста, через контекст, через анализ конкретной ситуации. Пример – определение уравнения в традиционном курсе математики.

Остенсивные определения – это определения путем показа. Они используются для введения терминов путем демонстрации объектов, которые этими терминами обозначают. Например, таким образом вводятся понятия равенства и неравенства в начальном курсе математики.

Уточнены представления о математических понятиях:

- это понятия об идеальных объектах;

- каждое математическое понятие имеет название (термин), объем и содержание;

- математические понятия могут находиться в отношении рода и вида, если их объемы находятся в отношении включения, но не совпадают;

- математические понятия могут быть тождественными, если их объемы совпадают;

- понятиям дают определения; они могут быть явными и неявными; к неявным относят контекстуальные и остенсивные определения; среди явных чаще используются определения через род и видовое отличие;

- при воспроизведении или конструировании определений через род и видовое отличие необходимо соблюдать ряд правил: определение должно быть соразмерным, в нем не должно быть порочного круга, оно должно быть ясным.

План:

1. Высказывания и высказывательные формы (предикат)

2. Конъюнкция и дизъюнкция высказываний

3. Конъюнкция и дизъюнкция высказывательных форм

Изучая реальные процессы, математика описывает их, используя как естественный словесный язык, так и свой символический. Описание строится при помощи предложений. Но чтобы математические знания правильно отражали окружающую нас реальность, эти предложения должны быть истинными.

Каждое математическое предложение характеризуется содержанием и логической формой (структурой), причем содержание неразрывно связано с формой, и нельзя осмыслить первое, не понимая второго.

1. Высказывания и высказывательные формы

Относительно понятий и отношений между ними можно высказывать различные суждения. Языковой формой суждений являются повествовательные предложения. Например, в начальном курсе математики можно встретить такие предложения:

1) число 12 – четное;

2) 2 + 5 > 8;

3) х + 5 = 8;

4) В числе 15 один десяток и 5 единиц;

5) От перестановки множителей произведение не изменяется;

6) Некоторые числа делятся на 3.

Видим, что предложения, используя в математике, могут быть записаны как на естественном (русском) языке, так и на математическом, с использованием символов. Далее, о предложениях 1, 4, 5 и 6 можно сказать, что они несут верную информацию, а предложение 2 – ложную. Относительно предложения х + 5 = 8 вообще нельзя сказать: истинное оно или ложное. Взгляд на предложение с позиции – истину или ложь оно нам сообщает – привел к понятию высказывания.

Определение. Высказыванием в математике называют предложение, относительно которого имеет смысл вопрос: истинно оно или ложно.

Например, предложения 1, 2, 4, 5 и 6 – высказывания, причем предложения 1, 4, 5 и 6 – истинные, а 2 – ложное.

Высказывания принято обозначать прописными буквами латинского алфавита: А, В, С, …, Z. Если высказывание А истинно, то записывают: А – «и», если же высказывание А – ложно, то пишут: А – «л».

«Истина» и «ложь» называются значениями истинности высказывания. Каждое высказывание либо истинно, либо ложно, быть одновременно тем и другим оно не может.

Предложение х + 5 = 8 не является высказыванием, так как о нем нельзя сказать: истинно оно или ложно. Однако при подстановке конкретных значений переменной х оно обращается в высказывание: истинное или ложное. Предложение х + 5 = 8 называется высказывательной формой. Оно порождает множество высказываний одной и той же формы.

По числу переменных, входящих в высказывательную форму, различают одноместные, двухместные и т.д. высказывательные формы и обозначают: А(х), А(х, у) и т.д. Например, предложение «Прямая х параллельна прямой у» - двухместная.

Определение. Одноместной высказывательной формой, заданной на множестве Х, называется предложение с переменной, которое обращается в высказывание при подстановке в него значений переменной из множества Х.

Множество Х – множество, из которого выбираются значения переменной.

Среди всех возможных значений переменной нас в первую очередь интересуют те, которые обращают высказывательную форму в истинное высказывание. Множество таких значений переменных называют множеством истинности высказывательной формы. Например, множеством истинности высказывательной формы х > 5, заданной на множестве действительных чисел, будет промежуток (5; ∞). Множество истинности высказывательной формы х + 5 = 8, заданной на множестве целых неотрицательных чисел, состоит из одного числа 3.

Условимся обозначать множество истинности высказывательной формы буквой Т. Тогда, согласно определению, всегда Т⊂Х.

Предложения, которые мы рассматривали, были простыми, но можно привести примеры суждений, языковой формой которых будут сложные предложения. Например: «Если треугольник равнобедренный, то углы при основании в нем равны». Естественно возникает вопрос: как определить значение истинности таких высказываний и находить множество истинности таких высказывательных форм?

Чтобы ответить на эти вопросы, необходимо познакомиться с некоторыми логическими понятиями.

В логике считают, что из двух данных предложений можно образовать новые предложения, используя для этого союзы «и», «или», «если…, то», «тогда и только тогда, когда», а также частица «не» или словосочетание «неверно, что». Слова «и», «или», «если…, то», «тогда и только тогда, когда», а также частица «не» называют логическими связками. Предложения, образованные из других предложений с помощью логических связок, называют составными. Предложения, не являющиеся составными, называют элементарными.

Приведем примеры составных предложений.

1) Число 28 четное и делится на 7.

2) Число х меньше или равно 8.

3) Число 14 не делится на 4.

Эти предложения, являясь с логической точки зрения составными, по своей грамматической структуре – простые.

Как определить значение истинности составного высказывания, например, «число 28 делится на 7 и на 9»? Значение истинности высказываний определяется с помощью определенных правил. Но для этого нужно уметь выявлять логическую структуру высказывания.

Для этого нужно установить:

1) из каких элементарных предложений образовано данное составное предложение;

2) с помощью каких логических связок оно образовано.

1. Конъюнкция и дизъюнкция высказываний

Определение. Конъюнкцией высказываний А и В называется высказывание А∧В, которое истинно, когда оба высказывания истинны, и ложно, когда хотя бы одно из высказываний ложно.

Обозначают А∧В (читают: «А и В»).

Определение конъюнкции можно записать с помощью таблицы, называемой таблицей истинности.

А	В	А∧В
и	и	и
и	л	л
л	и	л
л	л	л

Используя данное определение, найдем значение истинности высказывания «число 28 делится на 7 и на 9», которое, как было установлено раньше, состоит из двух элементарных высказываний, соединенных союзом «и», т.е. является конъюнкцией.. Так как первое высказывание истинно, а второе ложно, то, согласно определению конъюнкции, высказывание «число 28 делится на 7 и на 9» будет ложным.

Определение. Дизъюнкцией высказываний А и В называется высказывание А∨В, которое истинно, когда истинно хотя бы одно из этих высказываний, и ложно, когда оба высказывания ложны.

Высказывание образовано с помощью союза «или»: А∨В (читают А или В).

Используя данное определение, найдем значение истинности высказывания «число 28 делится на 7 или на 9». Так как это предложение является дизъюнкцией двух высказываний, одно из которых истинно, то, согласно определению дизъюнкции, высказывание «число 28 делится на 7 и на 9» будет истинным.

В математике союз «или» используется как неразделительный.

Образование составного высказывания с помощью логической связки называется логической операцией.

Определения конъюнкции и дизъюнкции можно обобщить на t составляющих их высказываний.

Конъюнкцией t высказываний называется предложение вида А₁ ∧ А₂ ∧…∧ Аt, которое истинно тогда и только тогда, когда истинны все составляющие его высказывания

Дизъюнкцией t высказываний называется предложение вида А₁ ∨ А₂ ∨…∨ Аt, которое ложно тогда и только тогда, когда ложны все составляющие его высказывания

1. Конъюнкция и дизъюнкция высказывательных форм

В математике рассматривают не только конъюнкцию и дизъюнкцию высказываний, но и выполняют соответствующие операции над высказывательными формами.

Конъюнкцию одноместных высказывательных форм А(х) и В(х), заданных на множестве Х, обозначают А(х) ∧ В(х). С появлением этого предложения возникает вопрос, как найти его множество истинности, зная множества истинности высказывательных форм А(х) и В(х). Другими словами, при каких значениях х из области определения Х высказывательная форма А(х) ∧ В(х) обращается в истинное высказывание? Очевидно, что это возможно при тех и только тех значениях х, при которых обращаются в истинное высказывание обе высказывательные формы А(х) и В(х). Если обозначить ТА – множество истинности предложения А(х), ТВ – множество истинности предложения В(х), а множество истинности их конъюнкции Т А∧В, то, по всей видимости, Т А∧В = ТА ∩ ТВ.

Докажем это равенство.

1. Пусть а – произвольный элемент множества Х и известно, что а ∈ Т А∧В. По определению множества истинности это означает, что высказывательная форма А(х) ∧ В(х) обращается в истинное высказывание при х = а, т.е. высказывание А(а) ∧ В(а) истинно. Так как данное высказывание конъюнкция, то получаем, что каждое из высказываний А(а) и В(а) также истинно. Это означает, что а ∈ Т А и а ∈ ТВ. Следовательно, по определению пересечения множеств, а ∈ ТА ∩ ТВ. Таким образом, мы показали, что Т А∧В ⊂ ТА ∩ ТВ.

2. Докажем обратное утверждение. Пусть а – произвольный элемент множества Х и известно, что а ∈ ТА ∩ ТВ. По определению пересечения множества это означает, что а ∈ Т А и а ∈ ТВ, откуда получаем, что А(а) и В(а) – истинные высказывания, поэтому конъюнкция высказываний А(а) ∧ В(а) также будет истинна. А это означает, что элемент а принадлежит множеству истинности высказывательной формы А(х) ∧ В(х), т.е.

а ∈ Т А∧В. Таким образом, мы доказали, что ТА ∩ ТВ ⊂ Т А∧В.

Из 1 и 2 в силу определения равных множеств вытекает справедливость равенства

Т А∧В = ТА ∩ ТВ, что и требовалось доказать.

Заметим, что полученное правило справедливо и для высказывательных форм, содержащих более одной переменной.

Дизъюнкцию одноместных высказывательных форм А(х) и В(х), заданных на множестве Х, обозначают А(х) ∨ В(х), Это предложение будет обращаться в истинное высказывание при тех и только тех значениях х из области определения Х, при которых обращается в истинное высказывание хотя бы одна из высказывательных форм, т.е.

Т А∨В = ТА ∪ ТВ. Доказательство этого равенства аналогично рассмотренному выше.

Приведем пример. Решим уравнение (х – 2) • (х + 5) = 0. Известно, что произведение равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю. Это означает, что данное уравнение равносильно дизъюнкции: х – 2 = 0 ∨ х + 5 = 0 и поэтому множество его решений может быть найдено как объединение множеств решения первого и второго уравнений, т.е {2}∪{-5} ={-5, 2}.

Заметим, что дизъюнкцию уравнений (неравенств) называют также совокупностью.

Рассматривая конъюнкцию и дизъюнкцию высказывательных форм, мы установили их тесную связь с пересечением и объединением множеств.

А∩В = {х\ х ∈А ∧ х∈В }, А∪В = {х\ х ∈А ∨ х∈В }, причем каждое свойство представляет собой высказывательную форму.

1. Решение задач на распознавание объектов

С введением понятия конъюнкции и дизъюнкции высказывательных форм появились условия для рассмотрения вопросов, связанных с решением определенного вида задач, так называемых задач на распознавание объектов.

В задачах на распознавание объектов требуется ответить на вопрос: принадлежит тот или иной объект объему данного понятия или не принадлежит.

Пример 1. «Установите, какие из фигур являются квадратами, а какие нет».

Решают такие задачи, используя определение соответствующего понятия. При этом важно понимать, что если понятие а определено через родовое понятие с и видовое отличие Р, то его объем А можно представить в таком виде: А = {х\ х ∈С и Р(х) } Эта запись показывает, что характеристическое свойство элементов, принадлежащих объему понятия а, представляет собой конъюнкцию двух свойств:

1) принадлежности объекта х объему С родового понятия (х ∈С);

2) свойства Р(х).

Пример 2. «Выяснить, в каком случае луч ВD является биссектрисой угла АВС».

Воспользуемся таким определением биссектрисы угла: «Биссектрисой угла называется луч, выходящий из вершины угла и делящий этот угол пополам». Из него следует, что для того, чтобы луч был биссектрисой угла, он должен обладать двумя свойствами: «выходить из вершины угла» и «делить этот угол пополам».

А D С А D С

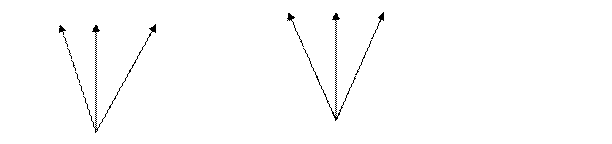
В В

а) б)

Луч ВD на рисунке а) не является биссектрисой угла АВС, поскольку он не делит данный угол пополам. Луч ВD на рисунке б) является биссектрисой угла АВС, поскольку он делит данный угол пополам и выходит из вершины угла.

Если видовое отличие представляет собой конъюнкцию свойств, т.е. Р = Р₁∧Р₂∧…∧Рn, то распознавание проводится по следующему правилу: проверяют поочередно наличие у объекта каждого из свойств Р₁, Р₂, …, Рn; если окажется, что он не обладает каким-либо из этих свойств, то проверку прекращают и делают вывод о том, что объект не обладает свойством Р; если же окажется, что все свойства Р₁, Р₂, …, Рn присущи данному объекту, то заключают, что объект обладает свойством Р.

Если видовое отличие представляет собой дизъюнкцию свойств, т.е. Р = Р₁∨Р₂∨…∨Рn, то распознавание проводится по следующему правилу: проверка проводится до тех пор, пока не будет установлено, что хотя бы одно из свойств присуще данному объекту, на основании чего заключают, что объект обладает свойством Р. Если окажется, что он не обладает ни одним из свойств Р₁, Р₂, …, Рn, то проверку прекращают и делают вывод о том, что объект не обладает свойством Р.

Дата добавления: 2014-01-06