Упражнения. 1. Используя материал данного параграфа, заполните следующую таблицу при условии, что решение задачи (РЗ) выполняется арифме­тическим методом,

1. Используя материал данного параграфа, заполните следующую таблицу при условии, что решение задачи (РЗ) выполняется арифме­тическим методом,

Название этапа РЗ	Цель этапа	Приемы выполнении этапа
Анализ задачи
Поиск плана решения
Осуществление плана решения
Проверка

2. Выполните анализ нижеприведенных задач, используя различ­ные приемы:

а) Ученик купил тетрадей в клетку в 3 раза больше, чем тетрадей в
линейку, причем их было на 18 больше, чем тетрадей в линейку.

Сколько всего тетрадей купил ученик?

б) В трех классах всего 83 учащихся. В первом классе на 4 ученика
больше, чем во втором, и на 3 меньше, чем в третьем. Сколько учеников в каждом классе?

в) Мальчики полили 8 яблонь и 4 сливы, принеся 140 ведер воды. Сколько ведер воды вылили под яблони, а сколько под сливы, если на
полив одной яблони уходит воды в 3 раза больше, чем на полив одной сливы.

3. Выполните поиск плана решения арифметическим методом за­дачи а) из упражнения 2 по модели, а поиск плана решения задачи в)
по тексту.

4. Запишите решение задачи из упражнения 2 по действиям с пояснением.

5. Какие из задач упражнения 2 вы можете решить различными
арифметическими способами?

6. Каким образом можно проверить правильность найденного результата для задачи а) из упражнения 2?

7. Решите арифметическим методом задачи, выделяя этапы решения и приемы их выполнения:

а) Ручка в два раза дороже карандаша, а резинка в три раза дешевле карандаша. Ручка, карандаш и резинка стоят вместе 4000 р. Сколько стоит резинка?

б) Сын на 24 года младше мамы, а папа на 3 года старше мамы.
Сколько лет папе, если сыну 10 лет?

в) Один кусок проволоки на 54 м длиннее другого. После того как от
каждого из кусков отрезали по 12 м, второй кусок оказался в 4 раза короче первого. Найдите первоначальную длину каждого куска проволок!)..

8. Дана задача: «Два велосипедиста одновременно выехали навстре­чу друг другу из двух поселков, расстояние между которыми 76 км.
Через 2 ч они встретились. Какова скорость каждого велосипедиста.
если известно, что скорость одного из них на 3 км/ч меньше другого»

Сравните разные способы ее решения.

1 способ 2 способ

1)76:2 = 38 (км/ч) 1)3∙2 = 6 (км)

2) 38 - 3 = 35 (км/ч) 2) 76 - 6 = 70 (км)

3) 35:2 = 17,5 (км/ч) 3) 70:2 = 35 (км)

4) 17,5 + 3 = 20,5 (км/ч) 4) 35:2. = 17,5 (км/ч)

5)17,5 +3 = 20,5 (км/ч)

При каком способе рассуждения проще?

Лекция 12. Текстовая задача и процесс ее решения

План:

1. Решение задач «на части»

2. Решение задач на движение

3. Основные выводы

32. Решение задач «на части»

Само название вида задач говорит о том, что рассматриваемые в них величины состоят из частей. В некоторых из них части представ­лены явно, в других эти части надо суметь выделить, приняв подхо­дящую величину за 1 часть и определив, из скольких таких частей состоят другие величины, о которых идет речь в задаче.

При решении таких задач арифметическим методом чаше всего ис­пользуют вспомогательные модели, выполненные с помощью отрез­ков или прямоугольников.

Задача 1. Для варки варенья из вишни на 2 части ягод берут 3 части сахара. Сколько сахара надо взять па 10 кг ягод?

Решение. В задаче речь идет о массе ягод и массе сахара, необхо­димых для варки варенья. Известно, что всего ягод 10 кг и что на 2 части ягод надо брать 3 части сахара. Требуется найти массу сахара. чтобы сварить варенье из 10 кг ягод.

Изобразим при помощи отрезка данную массу ягод (рис. 45). Тогда половина этого отрезка представляет собой массу ягод, которая приходится на 1 часть.

В 10 кг

С?

Рис. 45

Сахара, по условию задачи, надо 3 таких части. Запишем решение по действиям с пояснением:

1) 10:2 = 5 (кг) - столько килограммов ягод приходится на каждую часть;

2) 5 ×3 = 15 (кг) - столько надо взять сахара.
Вспомогательную модель к данной задаче можно было выполнить при помощи прямоугольников (рис. 46).

10 кг?

Рис. 46

Задача 2. В первой пачке было на 10 тетрадей больше, чем во вто­рой. Всего было 70 тетрадей. Сколько тетрадей было в каждой пачке?

Решение. В задаче рассматриваются две пачки тетрадей. Всего тетра­дей 70. В одной пачке тетрадей на 10 больше, чем во второй. Требуется узнать, сколько тетрадей было в каждой пачке.

Изобразим при помощи отрезка количество тетрадей во второй пачке. Тогда тетради в первой пачке можно представить в виде отрезка, который больше второго (рис. 47). По чертежу видно, что если тетради

10 т.

Рис. 47

во второй пачке составляют 1 часть всех тетрадей, то тетради в пер­вой составляют также 1 часть и еще 10 тетрадей.

Если эти 10 тетрадей убрать из первой пачки, то в пачках тетрадей станет поровну - столько, сколько во второй пачке.

Запишем решение задачи по действиям с пояснением.

1) 70-10 = 60 (тетр.) - столько тетрадей приходится на 2 равные части, или столько было бы тетрадей в двух пачках, если бы их было поровну - столько, сколько во второй пачке.

2) 60:2 = 30 (тетр.) - столько тетрадей приходится на 1 часть, или столько тетрадей было во второй пачке.

3) 30 +10 — 40 (тетр.) - столько тетрадей было в первой пачке.
Вспомогательная модель подсказывает и второй способ решения данной задачи. Если за I часть принять тетради в первой пачке, то чтобы во второй стало столько же, надо к ней добавить 10 тетрадей. И тогда решение будет таким:

1) 70+10 = 80 (тетр.)

2) 80:2 = 40 (тетр.)

3) 40-10 = 30 (тетр.)

Существует и третий арифметический способ решения данной за­дачи. Разделим 10 тетрадей пополам и одну половину оставим к пер­вой пачке, а другую добавим во вторую. Тогда тетрадей в пачках ста­нет поровну и можно, разделив 70 на 2 равные части, узнать, сколько тетрадей в каждой такой пачке, а затем их первоначальное количество в каждой пачке.

1) 10:2 = 5 (тетр.) - столько тетрадей надо переложить из первой
пачки во вторую, чтобы в них тетрадей стало поровну.

2) 70:2 = 35 (тетр.) - столько тетрадей в каждой пачке, если из первой переложить во вторую 5 тетрадей.

3) 35 + 5 = 40 (гетр.) - столько тетрадей в первой пачке.

4) 35-5 = 30 (тетр.) - столько тетрадей во второй пачке.
Задача 3. Сумма двух чисел 96, а разность 18. Найдите эти числа.
Решение. В этой задаче требуется найти два числа по их сумме и разности. Так как разность искомых чисел равна 18, то одно число больше другого на 18. Получаем задачу, аналогичную задаче 2: «Одно число больше другого па 18. Сумма чисел равна 96. Найти эти числам Решить ее можно тремя арифметическими способами.

Задача 4. В двух кусках ткани одинаковое количество материи. После того как от одного куска отрезали 18 м, а от другого 25 м, в первом куске осталось вдвое больше ткани, чем во втором. Сколько метров ткани было в каждом куске первоначально?

Решение. Объекты задачи - два куска ткани одинаковой длины От первого отрезали 18 м, от второго 25 м. После этого в первом осталось вдвое больше ткани, чем во втором. Требование задачи - найти первоначальное количество метров ткани в каждом куске.

Изобразим куски ткани при помощи отрезков одинаковой длины, а затем покажем на них то количество ткани, которое отрезали

18 м

I

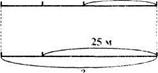
II

Рис. 48

и которое осталось. Если количе­ство ткани, которое осталось во втором куске, - это 1 часть, то количество оставшейся ткани в первом куске - это 2 таких части По чертежу (рис. 48) видно, что на 1 часть приходится количество ткани, которое легко найти. Запишем найденное решение по действиям:

1) 25-18 = 7 (м) - на столько больше ткани отрезали от второго
куска, или количество ткани, которое осталось во втором куске

2) 7 + 25 -- 32 (м) - столько ткани было первоначально во втором
куске (и, следовательно, в первом) куске.

Дата добавления: 2014-01-06