Решение задач на движение

Движение является темой для самых разнообразных задач, в том числе и для задач на части. Но наряду с этим существует и самостоя­тельный тип задач на движение. Он объединяет такие задачи, которые решаются па основании зависимости между тремя величинами, харак­теризующими движение: скоростью, расстоянием и временем. Во всех случаях речь идет о равномерном прямолинейном движении.

Итак, движение, рассматриваемое в текстовых задачах, характери­зуют три величины: пройденный путь (s), скорость (v), время (t); ос­новное отношение (зависимость) между ними: s = v ∙ t.

Рассмотрим особенности решения основных видов задач на дви­жение.

Задачи на встречное движение двух тел

Пусть движение первого тела характеризуется величинами s₁, v₁, t₁, движение второго - s₂, v₂, t₂,. Такое движение можно представить на схематическом чертеже (рис. 50):

Рис. 50

Если два объекта начинают движение одновременно навстречу друг другу, то каждое из них с момента выхода и до встречи затрачивает одинаковое время, т.е. t₁, = t₂ = t _вапр.

Расстояние, на которое сближаются движущиеся объекты за еди­ницу времени, называется скоростью сближения, т.е. vсбл. = v ₁+ v₂.

Все расстояние, пройденное движущимися телами при встречном движении, может быть подсчитано по формуле: s = vсбл.∙ t _вапр

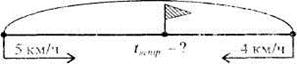
Задача 1. Два пешехода одновременно вышли навстречу друг другу из двух пунктов, расстояние между которыми 18 км. Скорость одного из них 5 км/ч, а другого - 4 км/ч. Через сколько часов они встретились?

Решение. В задаче рассматривается движение навстречу друг
другу двух пешеходов. Один идет со скоростью 5 км/ч, а другой -
4 км/ч. Путь, который они должны пройти, 18 км. Требуется найти время, через которое

они встретятся, начав движение одновременно. Вспомогательные модели,
если они нужны, могут быть разными - схематический чертеж
(рис. 51) или таблица.

Поиск плана решения в данном случае удобно вести, рассуждая от данных к вопросу. Так как ско­рости пешеходов известны, можно найти их скорость сближения. Зная скорость сближения пешеходов и все расстояние, которое им надо пройти, можем найти время, через которое пешеходы встретятся. Запишем решение задачи по действиям:

1)5+ 4 = 9 (км/ч)

2) 18:9 = 2(ч) Таким образом, пешеходы встретятся через 2 ч от начала движения.

Задача 2. Два автомобиля выехали одновременно навстречу друг другу из двух пунктов, расстояние между которыми 600 км, и через 5 ч встретились. Один их них ехал быстрее другого на 16 км/ч. Опреде­лите скорости автомобилей.

Решение. В задаче рассматривается движение навстречу друг другу двух автомобилей. Известно, что движение они начали одновременно и встретились через 5 часов. Скорости автомобилей различны один ехал быстрее другого на 16 км/ч. Путь, который проехали автомобили -600 км. Требуется определить скорости движения.

	s	v	t
I II	600 км	? ? на 16 км/ч больше	5 ч 5 ч

Вспомогательные модели, если они нужны, могут быть различ­ными: схематический чертеж (рис. 52) или таблица.

Поиск плана решения задачи будем вести, рассуждая от дан­ных к вопросу. Так как известно все расстояние и время встречи, можно найти скорость сближе­ния автомобилей. Затем, зная, что скорость одного на 16 км/ч больше скорости другого, можно найти скорости автомобилей. При этом можно воспользоваться вспомогательной моделью.

Запишем решение:

1) 600:5= 120 (км/ч) – скорость сближения автомобилей

2) 120 - 16 = 104 (км/ч) – скорость сближения, если бы скорость автомобилей была одинаковой

3) 104:2 =52 (км/ч) – скорость первого автомобиля.

4) 52 + 16 = 68 (км/ч) – скорость второго автомобиля.

Есть и другие арифметические способы решения данной задачи, вот два из них.

1) 600:5= 120 (км/ч) 1) 16-5 = 80 (км)

2) 120 + 16 = 136 (км/ч) 2) 600 - 80 = 520 (км)

3) 136:2 = 68 (км/ч) 3) 520:2 = 260 (км)

4) 68 -16 = 52 (км/ч) 4) 260:5 = 52 (км/ч)

5)52+ 16 = 68 (км/ч)

Дайте устные пояснения к выполненным действиям и попытайтесь найти другие способы решения данной задачи.

Задачи на движение двух тел в одном направлении

Среди них следует различать два типа задач:

1) движение начинается одновременно из разных пунктов;

2) движение начинается в разное время из одного пункта.

Рассмотрим случай, когда движение двух тел начинается одновре­менно в одном направлении из разных пунктов, лежащих на одной прямой. Пусть движение первого тела характеризуется величинами s₁, v₁, t₁, движение второго - s₂, v₂, t₂,.

Такое движение можно представить на схематическом чертеже (рис 54):

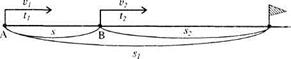
Рис. 54

Если при движении в одном направлении первое тело догоняет второе, то v₁ > v₂. Кроме того, за единицу времени первый объект приближается к другому на расстояние

v₁ - v₂.. Это расстояние назы­вают скоростью сближения: vсбл. = v₁ - v₂..

Расстояние s, представляющее длину отрезка АВ, находят по фор­мулам:

s = s₁ - s₂ и s = vсбл. ∙ tвстр.

Задача 3. Из двух пунктов, удаленных друг от друга на 30 км, выехали одновременно в одном направлении два мотоциклиста. Ско­рость одного - 40 км/ч, другого - 50 км/ч. Через сколько часов второй мотоциклист догонит первого?

Решение. В задаче рассматривается движение двух мотоцикли­стов. Выехали они одновременно из разных пунктов, находящихся на расстоянии 30 км. Скорость одного 40 км/ч, другого - 50 км/ч. Требует­ся узнать, через сколько часов второй мотоциклист догонит первого.

Вспомогательные модели, если они нужны, могут быть разными: схематический чертеж или таблица.

Сравнение скоростей мотоцик­листов говорит о том, что в тече­ние часа первый мотоциклист при­ближается ко второму на 10 км Расстояние, которое ему надо пройти до встречи со вторым, на 30 км больше, чем расстояние, ко­торое за такое же время пройдет второй мотоциклист. Поэтому первому потребуется столько времени, сколько раз 10 км укладываются в 30 км. Запишем решение задачи по действиям:

1) 50 - 40 = 10 (км/ч) - скорость сближения мотоциклистов

2) 30:10 = 3 (ч) - за это время первый мотоциклист догонит второго.
Наглядно этот процесс представлен на рисунке 56, где единичный отрезок изображает расстояние, равное 10 км.

40 км/ч

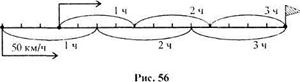
Задача 4. Всадник выезжает из пункта А и едет со скоростью 12 км/ч; в это же время из пункта В, отстоящего от А на 24 км, вышел пешеход со скоростью 4 км/ч. Оба движутся в одном направлении На каком расстоянии от В всадник догонит пешехода?

Решение. В задаче рассматривается движение в одном направле­нии всадника и пешехода. Движение началось одновременно из раз­ных пунктов, расстояние между которыми 24 км, и с разной скоро­стью: у всадника - 12 км/ч, у пешехода - 4 км/ч. Требуется узнать рас­стояние от пункта, из которого вышел пешеход, до момента встречи всадника и пешехода.

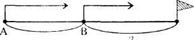Вспомогательные модели: схе­матический чертеж (рис. 57) или таблица.

24 км

Чтобы ответить на вопрос зада­чи, надо найти время, которое будет находиться в пути пешеход или всадник, - время их движения до встречи одинаковое. Как найти это время, подробно рассказано в пре­дыдущей задаче. Поэтому, чтобы от­ветить на вопрос задачи, необходи­мо выполнить следующие действия:

1) 12-4 = 8 (км/ч) - скорость сближения всадника и пешехода.

2) 24:8 = 3 (ч) - время, через которое всадник догонит пешехода

3) 4 ∙ 3 - 12 (км) - расстояние от В, на котором всадник догонит пешехода.

Задача 5. В 7 ч из Москвы со скоростью 60 км/ч вышел поезд. В 13 ч следующего дня в том же направлении вылетел самолет со скоро­стью 780 км/ч. Через какое время самолет догонит поезд?

Решение. В данной задаче рассматривается движение поезда и самолета в одном направлении из одного пункта, но начинается оно в разное время. Известны скорости поезда и самолета, а также время начала их движения. Требуется найти время, через которое самолет догонит поезд.

Из условия задачи следует, что к моменту вылета самолета поезд прошел определенное расстояние. И если его найти, то данная задача становится аналогичной задаче 3, рассмотренной выше.

Чтобы найти расстояние, которое прошел поезд до момента выле­та самолета, надо подсчитать, сколько времени находился в пути по­езд. Умножив время на скорость поезда, получим расстояние, прой­денное поездом до момента вылета самолета. А дальше как в задаче 3.

1) 24 - 7 - 17 (ч) - столько времени был в пути поезд в тот день, когда он вышел из Москвы.

2) 17 + 13 = 30 (ч) - столько времени был в пути поезд до момента
вылета самолета.

3) 60 ∙ 30 - 1800 (км) - путь, пройденный поездом до момента вылета самолета.

4) 780 - 60 = 720 (км/ч) - скорость сближения самолета и поезда.

5) 1800:720 = 2—(ч)-время, через которое самолет догонит поезд.

Задачи на движение двух тел в противоположных направлениях

В таких задачах два тела могут начинать движение в противополож­ных направлениях из одной точки: а) одновременно; б) в разное время. А могут начинать свое движение из двух разных точек, находящихся на заданном расстоянии, и в разное время.

Общим теоретическим положением для них будет следующее: vудал. = v₁ + v₂.. соответственно скорости первого и второго тел, а v удал. - это скорость удаления, т.е. расстояние, на которое удаля­ются друг от друга движущиеся тела за единицу времени.

Задача 6. Два поезда отошли одновременно от одной станции в противоположных направлениях. Их скорости 60 км/ч и 70 км/ч. На каком расстоянии друг от друга будут эти поезда через 3 часа после выхода?

Решение. В задаче рассматривается движение двух поездов. Они выходят одновременно от одной станции и идут в противоположных направлениях. Известны скорости поездов (60 км/ч и 70 км/ч) и время их движения (3 ч). Требуется найти расстояние, на котором они будут находиться друг от друга через указанное время.

Вспомогательные модели, если они нужны, могут быть такими: схематический чертеж или таблица.

Чтобы ответить на вопрос за­дачи, достаточно найти расстоя­ния, пройденные первым и вто­рым поездом за 3 ч, и полученные результаты сложить:

1)60 ∙ 3= 180 (км)

2) 70 ∙ 3 = 210 (км)

3) 180 + 210 = 390 (км)
Можно решить эту задачу другим способом, воспользовавшись понятием скорости удаления:

1) 60 + 70 = 130 (км/ч) - скорость удаления поездов

2) 130 ∙3 = 390 (км) - расстояние между поездами через 3 ч.
Задача 7. От станции Л отправился поезд со скоростью 60 км/ч

Через 2 ч с этой же станции в противоположном направлении вышел другой поезд со скоростью 70 км/ч. Какое расстояние будет между поездами через 3 ч после выхода второго поезда?

Решение. Эта задача отличается от задачи 6 тем, что движение поездов начинается в разное время. Вспомогательная модель задачи представлена на рис. 59. Решить ее можно двумя арифметическими способами.

60 км/ч 70 км/ч

Рис, 59

1 способ

1) 2 + 3 = 5 (ч) - столько времени в пути был первый поезд.

2) 60 5 ∙ 300 (км) - расстояние, которое за 5 ч прошел этот поезд.

3) 70 ∙ 3 - 210 (км) - расстояние, которое прошел второй поезд.

4) 300 + 210 = 510 (км) - расстояние между поездами.

2 способ

1) 60 + 70 = 130 (км/ч) - скорость удаления поездов.

2) 130 ∙ 3 = 390 (км) расстояние, на которое удалились поезда за 3 ч.

3) 60 ∙ 2 = 120 (км) - расстояние, пройденное первым поездом за 2 ч.

4) 390 + 120 = 510 (км) - расстояние между поездами.

Задачи на движение по реке

При решении таких задач различают: собственную скорость дви­жущегося тела, скорость течения реки, скорость движения тела по течению и скорость движения тела против течения. Зависимость меж­ду ними выражается формулами:

vпо теч. = vсбл. + vтеч.р.;

vпр. теч. = vсбл. – vтеч.р.

vсбл. = (vтеч.р + vпр. теч.): 2.

Задача 8. Расстояние 360 км катер проходит за 15 ч, если двигает­ся против течения реки, и за 12 ч, если двигается по течению. Сколько времени потребуется катеру, чтобы проплыть 135 км по озеру?

Решение. В данном случае удобно все данные, неизвестные и ис­комое, записать в таблицу.

	s	v	t
по течению	360 км		12 ч
против течения	360 км		15 ч
по реке	135 км	?

Таблица подсказывает последовательность действий: найти сначала скорость движения катера по течению и против течения, затем, исполь­зуя формулы, - собственную скорость катера и, наконец, время, за ко­торое он проплывет 135 км по озеру:

1) 360:12 = 30 (км/ч) - скорость катера по течению реки.

2) 360:15 — 24 (км/ч) - скорость катера против течения реки.

3) 24 + 30 - 54 (км/ч) - удвоенная собственная скорость катера.

4) 54:2 = 27 (км/ч) - собственная скорость катера

5) 135: 27 = 5 (ч) - время, за которое проплывет катер 135 км.

Р е ш е н и е з а д а ч, с в я з а н н ы х с р а з л и ч н ы м и

п р о ц е с с а м и (работа, наполнение бассейнов и др.)

Задача 9. Двум рабочим дано задание изготовить 120 деталей. Один рабочий зготавливает 7 деталей в час, а другой - 5 деталей в час. За сколько часов рабочие выполнят задание, работая вместе?

Решение. В задаче рассматривается процесс выполнения двумя ра­бочими задания по изготовлению 120 деталей. Известно, что одни рабочий делает в час 7 деталей, а другой - 5. Требуется узнать время, за которое рабочие сделают 120 деталей, работая вместе. Чтобы найти ответ на это требование, надо знать, что процесс, о котором идет речь в задаче, характеризуется тремя величинами:

- общим количеством произведенных деталей это результат про­цесса; обозначим его буквой К;

- количеством изготовленных деталей за единицу времени (это производительность труда или скорость протекания процесса); обо­значим его буквой к;

- временем выполнения задания (это время протекания процесса), обозначим его буквой t.

Зависимость между данными величинами выражается формулой К=кt.

Чтобы найти ответ на вопрос задачи, т.е. время t надо найти коли­чество деталей, изготавливаемых рабочими за 1 ч при совместной ра­боте, а затем разделить 120 деталей на полученную производитель­ность. Таким образом, будем иметь: к = 7 + 5 = 12 (деталей в час):,

T = 120:12= 10 (ч).

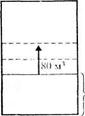
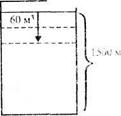
Задача 10. В одном резервуаре 380 м³ воды, а в другом - 1500 м ^3. В первый резервуар каждый час поступает 80 м³ воды, а из второго каждый час выкачивают по 60 м³ воды. Через сколько часов в резер­вуарах воды станет поровну?

Решение. В данной задаче рассматривается процесс заполнения водой одного резервуара и выкачивания воды из другого. Этот про­цесс характеризуется следующими величинами:

- объемом воды в ре­зервуарах; обозначим его буквой V;

- скоростью поступления (накачивания) воды; об о з н а ч и м его б у к в о й v;

- временем протекания процесса; обозначим его буквой t

380 м^{3 1500} м³

Зависимость между названными величинами выражается форму­лой V = v ∙ t

Процесс, описанный в данной задаче, аналогичен движению двух объектов навстречу друг другу. Это можно наглядно представить, по­строив вспомогательную модель (рис. 60).

Чтобы ответить на вопрос задачи, надо найти скорость «сближе­ния» уровней воды в резервуарах и объем воды, при котором проис­ходит выравнивание этих уровней, а затем разделить этот объем на скорость «сближения». Запишем решение задачи по действиям:

1)80 + 60 = 140 (мЗ);

2) 1500 – 380 = 1120 (м³):

3) 1120:140 = 8(ч).

Чтобы убедиться в правильности полученного ответа, выполним проверку.

За 8 ч в первый резервуар поступит 640 м³ (80 ∙ 8 = 640), а из второ­го выкачают

480 м³ (60 ∙ 8 = 480). Тогда в первом воды будет 1020 м³ (380 + 640 = 1020), и во втором - столько же (1500 - 480 = 1020), что удовлетворяет условию задачи.

Дата добавления: 2014-01-06