Лекция 5. Кинематика зубчатых передач с неподвижными осями

Кинематика зубчатых передач с неподвижными осями

В зубчатых передачах вращение осуществляется зацеплением специально профилированных зубьев, при этом на каждом из зубчатых колес имеются окружности, называемые начальными, которые перекатываются друг по другу без скольжения.

В точке А касания начальных окружностей с радиусами r₁ и r₂ (рис.11) окружная скорость рассчитывается так:

.

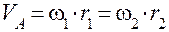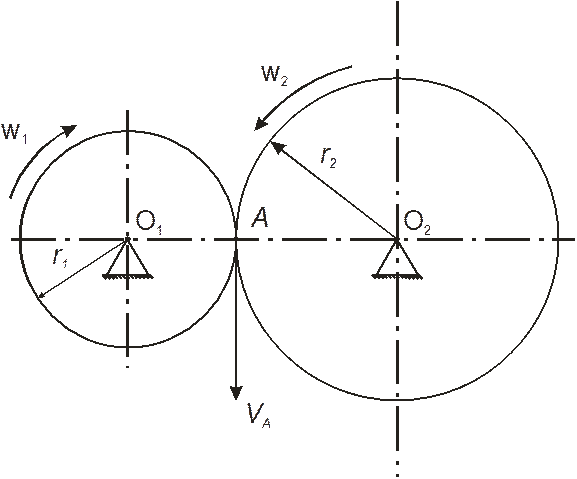
Рис.11

При отсутствии скольжения передаточное отношение вычисляется по формуле

.

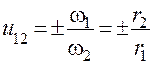При внешнем зацеплении – знак минус; при внутреннем зацеплении – знак плюс.

Одним из основных параметров зубчатого зацепления является модуль. При этом

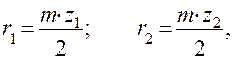
где m – модуль зацепления;

z₁, z₂ – числа зубьев колес.

Таким образом

.

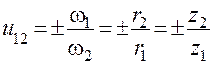Одноступенчатая зубчатая передача (рис..6,7,8) позволяет реализовать передаточное отношение 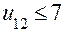. При больших передаточных отношениях используют многоступенчатые передачи, например трехступенчатые (рис. 12).

Ведущим в передаче является колесо 1, ведомым – 6, общее передаточное отношение:

.

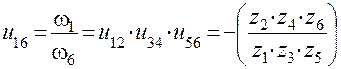Действительно,

но ω₂ = ω ₃, ω₄ = ω₅, поскольку колеса 2,3 и 4,5 закреплены на единых валах. Таким образом:

.

Для пространственных передач (например, конических) величина передаточного отношения определяется аналогично вышеизложенному.

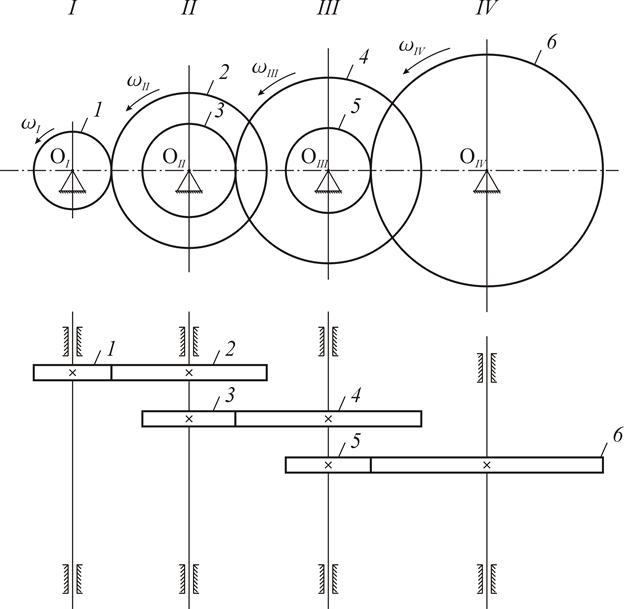Рис.12

Что касается знака, то для одноступенчатой передачи он не рассматривается, а для многоступенчатой имеет смысл только в том случае, если оси ведущего и ведомого колес параллельны.

В этом случае можно использовать метод стрелок, в соответствии с которым в точке касания начальных окружностей стрелки, символизирующие скорости, либо сходятся, либо расходятся. Тогда по взаимному расположению стрелок на ведущем и ведомом колесах определяют знак общего передаточного отношения: сонаправлены – плюс (рис. 14), противонаправлены – минус (рис. 13).

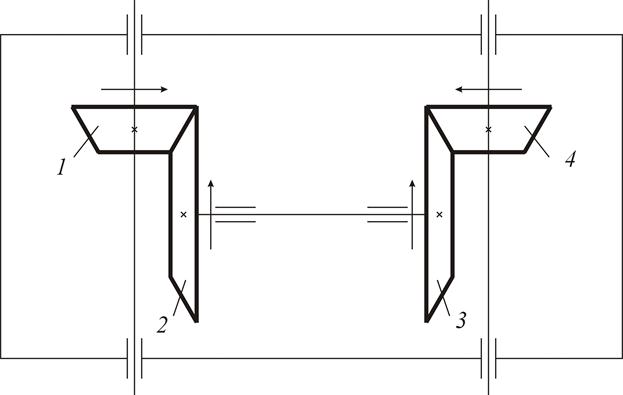Рис.13

.

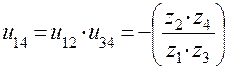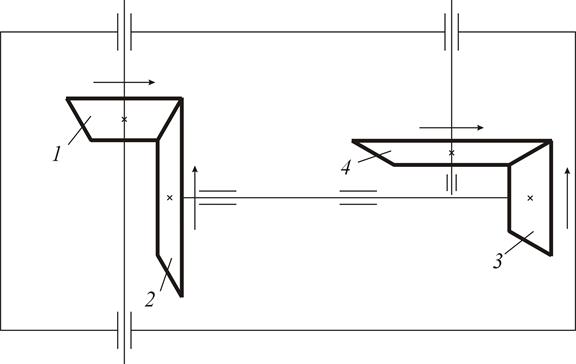
Рис.14

.

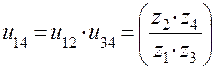Кинематика планетарных и дифференциальных редукторов

Передаточные отношения механизмов, у которых имеются зубчатые колеса с подвижными осями (рис..10), определяют с помощью метода обращенного движения.

Для этого механизму мысленно придают дополнительную угловую скорость, равную по величине и противоположную по направлению угловой скорости водила – ω_н. Это не изменит относительного движения звеньев, абсолютные же скорости будут другими:

Звено				H
Скорость в истинном движении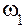
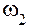
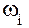
Скорость в обращенном движении

Таким образом, в обращенном движении водило останавливается и дифференциальный или планетарный механизм преобразуются в механизм с неподвижными осями вращения зубчатых колес, для которого справедливо отношение

.

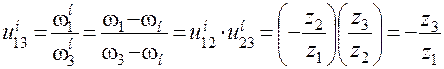При решении практических задач по определению передаточных отношений дифференциальных редукторов в исходных данных должны быть указаны числа зубьев всех зубчатых колес и угловые скорости двух звеньев.

Для планетарных редукторов, в которых одно из центральных колес закреплено, достаточно знать числа зубьев зубчатых колес.

Например, при неподвижном центральном колесе 3, ω₃=0. Тогда

;

.

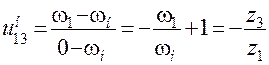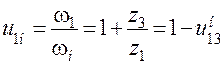Как видно из рис./10, зубчатый механизм может быть работоспособным только в том случае, если оси вращения центральных колес и водила совпадают. Это называется условием соосности, из которого следует:

;

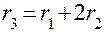При равенстве модулей всех зубчатых зацеплений:

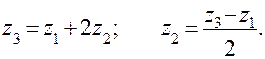
Таким образом, если в исходных данных задачи по определению передаточного отношения не указано число зубьев одного из зубчатых колес, его можно найти по условию соосности.

Кроме условия соосности, при проектировании планетарных и дифференциальных редукторов должна быть проведена проверка по выполнению еще двух условий:

Рис. 15

1. Условие соседства

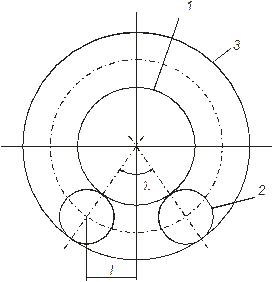
При сборке редуктора соседние сателлиты не должны касаться друг друга (рис.15).

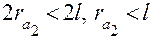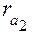Это будет при выполнении условия , где – радиус окружности вершин зубьев сателлита.

,

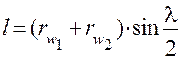где 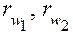– радиусы начальных окружностей центрального колеса_1 и сателлита_2.

λ – угол между осями соседних сателлитов

,

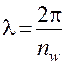где – количество сателлитов.

Таким образом, условие соседства имеет вид:

.

Если не учитывать смещение исходного контура при нарезании зубьев (x.=.0), то с достаточной степенью точности можно принять

,

где 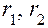– радиусы делительных окружностей центрального колеса 1 и сателлита 2.

Таким образом,

.

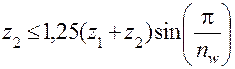2. Условие сборки

При сборке механизма, имеющего несколько сателлитов, зубья этих сателлитов должны полностью совпадать с впадинами зубьев центральных колес 1 и 3. Это будет выполняться при условии

,

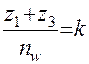где k – целое число.

Таким образом, сумма чисел зубьев центральных колес должна быть кратна числу сателлитов.

Дата добавления: 2014-01-06