
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Основные сведения о комплексных числах
|
|
|
|
Комплексным числом называется выражение вида
 , (2.6)
, (2.6)
где 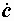 – обозначение комплексного числа; a и b – соответственно действительная и мнимая части комплексного числа;
– обозначение комплексного числа; a и b – соответственно действительная и мнимая части комплексного числа;  – мнимая единица.
– мнимая единица.
Величины a и b часто обозначают следующим образом: a = Re 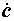 , b = Im
, b = Im 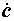 . Символы Re и Im – есть начальные буквы английских слов Real – действительный и Imaginary – мнимый.
. Символы Re и Im – есть начальные буквы английских слов Real – действительный и Imaginary – мнимый.
| Геометрически комплексное число изображается вектором на комплексной плоскости (рис. 2.8). Горизонтальная и вертикальная оси, отмеченные соответственно знаками + и + j, называются действительной (или вещественной) и мнимой. Действительная и мнимая составляющие комплексного числа представляют собой проекции вектора на эти оси. | 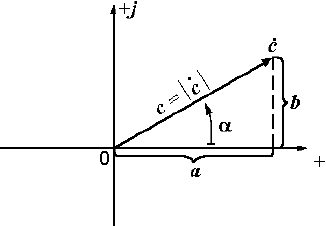 Рис. 2.8. Вектор на комплексной плоскости
Рис. 2.8. Вектор на комплексной плоскости
|
На рис. 2.8 с = c 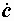 c – модуль комплексного числа, равный длине вектора, а a = arg
c – модуль комплексного числа, равный длине вектора, а a = arg 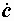 – аргумент комплексного числа. Так как а = c cosa, а
– аргумент комплексного числа. Так как а = c cosa, а
b = c sina, то 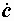 = c (cosa + j sina) – тригонометрическая форма комплексного числа. С помощью формулы Эйлера
= c (cosa + j sina) – тригонометрическая форма комплексного числа. С помощью формулы Эйлера  последняя преобразуется в показательную форму
последняя преобразуется в показательную форму  . Применяется еще и полярная форма
. Применяется еще и полярная форма 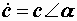 , в самой простой форме задающая модуль и аргумент комплексного числа.
, в самой простой форме задающая модуль и аргумент комплексного числа.
Свойства мнимой единицы (рис. 2.9):
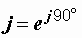 , ,  , ,
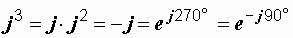 , ,
 , ,
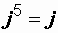 и т.д., и т.д.,
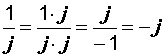 . .
| 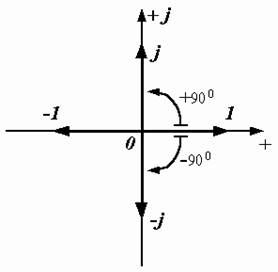 Рис. 2.9. Единичный вектор в комплексной плоскости
Рис. 2.9. Единичный вектор в комплексной плоскости
|
Два комплексных числа  и
и  называются сопряженными, если они имеют одинаковые модули и равные по величине, но разные по знаку аргументы (рис. 2.10):
называются сопряженными, если они имеют одинаковые модули и равные по величине, но разные по знаку аргументы (рис. 2.10):
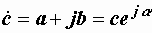 , ,
 = =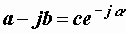 .
Изображающие их векторы симметричны относительно вещественной оси.
Действия над комплексными числами.
Сложение и вычитание производится над числами, записанными в алгебраической форме: .
Изображающие их векторы симметричны относительно вещественной оси.
Действия над комплексными числами.
Сложение и вычитание производится над числами, записанными в алгебраической форме:
| 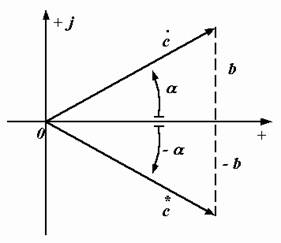 Рис. 2.10. Сопряженные комплексные числа
Рис. 2.10. Сопряженные комплексные числа
|
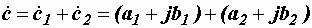 =
=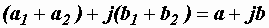 , т.е. складываются по отдельности вещественные и мнимые части слагаемых: а = а1 + а2, b = b1 + b2. Операции сложения комплексных чисел соответствует сложение изображающих их векторов.
, т.е. складываются по отдельности вещественные и мнимые части слагаемых: а = а1 + а2, b = b1 + b2. Операции сложения комплексных чисел соответствует сложение изображающих их векторов.
Сумма сопряженных комплексных чисел равна удвоенному значению вещественной части:
 +
+ =
=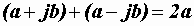 .
.
Умножение и деление комплексных чисел удобнее всего производить в показательной форме. Модули при этом перемножаются или делятся, а аргументы складываются или вычитаются:
 (2.7)
(2.7)
где с = с1 с2, a =a 1 +a 2;
 ,
,
где  , a =a 1 – a 2.
, a =a 1 – a 2.
Что происходит с векторами при перемножении комплексных чисел?
Изобразим на комплексной плоскости два вектора: 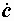 1 – первый сомножитель и
1 – первый сомножитель и 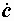 – результирующий (рис. 2.11). Последний получается умножением
– результирующий (рис. 2.11). Последний получается умножением 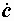 1 на комплексное число с2е ja 2.
1 на комплексное число с2е ja 2.
| На рис. 2.11 мы видим, что при умножении длина вектора возросла в с2 раз, а аргумент увеличился на a 2. Рассматривая комплексное число как вектор, мы приходим к следующему выводу. При умножении вектора на комплексное число ае ja , вектор растягивается в а раз и поворачивается на угол a. |  Рис. 2.11. Перемножение комплексных чисел
Рис. 2.11. Перемножение комплексных чисел
|
Так как  , то при умножении вектора на ± j он поворачивается на угол ± 90° (рис. 2.12).
, то при умножении вектора на ± j он поворачивается на угол ± 90° (рис. 2.12).
Произведение сопряженных комплексных чисел равно квадрату модуля комплексного числа:
 x x   ,
или ,
или
   Иногда приходится производить умножение и деление комплексных чисел в алгебраической форме. Перемножение выполняется по правилам умножения многочленов с учетом того, что j2 = -1
Иногда приходится производить умножение и деление комплексных чисел в алгебраической форме. Перемножение выполняется по правилам умножения многочленов с учетом того, что j2 = -1
| 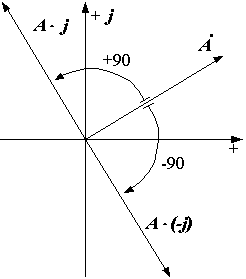 Рис. 2.12. Умножение вектора на ± j
Рис. 2.12. Умножение вектора на ± j
|
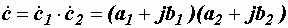 =
=
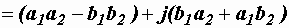 .
.
При делении, чтобы получить результат, необходимо избавиться от мнимой единицы в знаменателе. Этого можно достичь умножением числителя и знаменателя на сопряженный знаменатель:

где  ;
;  .
.
2.6. Представление синусоидальных функций времени
комплексными числами
Пусть задано выражение синусоидального тока i = Imsin(w t+y). Как мы видели раньше, этому выражению соответствует вектор, длина которого равна Im, а угол наклона к горизонтальной оси y. Если этот вектор изобразить в комплексной плоскости (рис. 2.13), то его можно обозначить комплексным числом 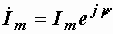 , которое называется комплексной амплитудой тока. , которое называется комплексной амплитудой тока.
| 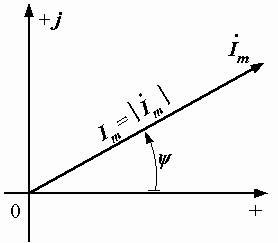 Рис. 2.13. Вектор тока на комплексной плоскости
Рис. 2.13. Вектор тока на комплексной плоскости
|
Комплексное действующее значение тока получается делением последнего выражения на 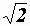 :
:
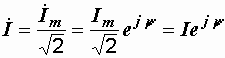 .
.
Здесь и дальше буквами с точкой над ними ( ) обозначаются комплексные числа, представляющие синусоидальные функции времени. Это ток, напряжение и ЭДС. Комплексные сопротивление и проводимость обозначаются прописными буквами Z и Y, а их модули строчными z и y. Комплексная мощность обозначается буквой S с волнистым значком ~ (тильда) над ней:
) обозначаются комплексные числа, представляющие синусоидальные функции времени. Это ток, напряжение и ЭДС. Комплексные сопротивление и проводимость обозначаются прописными буквами Z и Y, а их модули строчными z и y. Комплексная мощность обозначается буквой S с волнистым значком ~ (тильда) над ней:  .
.
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 453; Нарушение авторских прав?; Мы поможем в написании вашей работы!