Резонансные режимы двухполюсника

Резонанс – это такой режим электрической цепи, содержащей емкости и индуктивности, при котором общее входное сопротивление или входная проводимость цепи будут чисто активным. В этом режиме цепь потребляет только активную мощность и входные ток и напряжение совпадают по фазе. Различают резонансы напряжений, токов в сложной цепи.

Резонанс напряжений – это резонанс при последовательном соединении участков цепи с индуктивным и емкостным характером (рис. 3.1).

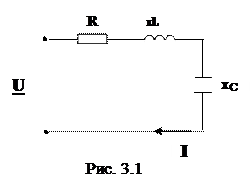Общее сопротивление цепи . Исходя из определения резонанса запишем условие резонанса: или . В режиме резонанса напряжений за счет компенсации реактивных сопротивлений входное сопротивление цепи будет активным и наименьшим 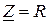, следовательно, общий ток станет максимальным: .

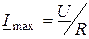Резонанс напряжений может быть достигнут изменением частоты, емкости или индуктивности:

- если заданы L и C, то резонансная угловая частота ;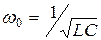

- если заданы L и 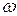, то резонансная емкость ;

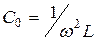- если заданы С и 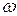, то резонансная индуктивность .

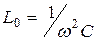Напряжения на реактивных элементах , будут равны по модулю (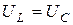) и могут значительно превосходить по величине приложенное напряжение. Угол между входным напряжением и током в режиме резонанса записывается в виде 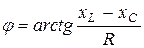и равен нулю. Следовательно, реактивная мощность цепи также равна нулю, и цепь в режиме резонанса потребляет только активную мощность .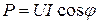

При оценке электрических цепей в их способности подавлять или передавать электрические сигналы широко используются частотные характеристики – зависимости параметров цепи от частоты - которые полностью определяют поведение цепи при ее питании от источников периодических сигналов. Различают амплитудно-частотные характеристики (АЧХ) – это зависимости амплитуд или действующих значений параметров цепи от частоты и фазо-частотные (ФЧХ) – зависимости фаз от частоты. Резонанс

но- частотные характеристики 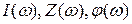представлены на рис. 3.2.

Рис. 3.2

Как видно из рис. 3.2, входной ток при резонансе резко изменяет свою величину, что приводит к частотным искажениям сигнала. Чтобы эти искажения не превышали нормы, спектр сигнала не должен выходить за пределы полосы пропускания , которая определяется по уровню 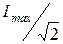резонансной кривой тока 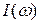. По полосе пропускания определяется качество резонансной цепи – ее добротность: . Добротность контура определяет, во сколько раз напряжение на реактивных элементах при резонансе превышает входное:

,

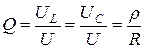где - характеристическое сопротивление.

Векторная диаграмма резонанса напряжений представлена на рис. 3.3.

Пример 3.1. В контуре с добротностью Q = 1.73 (рис. 3.4) определить напряжение U_V1, если входное напряжение при резонансе 1 В.

Решение. В последовательном колебательном контуре при резонансе UВХ = U = UR, следовательно,
UR = 1В. Добротность цепи при резонансе напряжений определяется как
Q = UL/U, значит UL=QU= 1.73B. Напряжение на вольтметре V1 запишется в виде

UV1 = 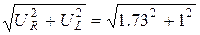=2 В.

Резонанс токов – это резонанс при параллельном соединении участков цепи с индуктивным и емкостным характером.

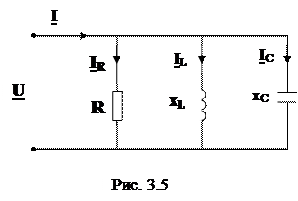
Пусть на вход цепи подано напряжение 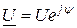(рис. 3.5), тогда токи в параллельных ветвях определятся по закону Ома:

; ; ,

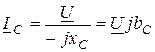где ; ; 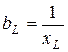- проводимости ветвей (1/Ом = См).

Общий ток по первому закону Кирхгофа запишется в виде

,

где 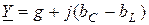- комплекс полной проводимости цепи.

Исходя из общего определения резонанса, запишем условие резонанса токов: 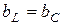или 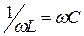. В виду того, что реактивные проводимости в режиме резонанса компенсируют друг друга, то результирующая проводимость будет минимальна. Следовательно, при неизменном приложенном напряжении входной ток будет минимальным.

Изменяя частоту при заданном входном напряжении и параметрах цепи, можно построить частотные характеристики (рис. 3.6).

При 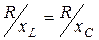>> 1 токи и 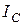могут значительно превосходить общий ток. Угол между входным током и приложенным напряжением 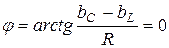, значит, реактивная мощность в режиме резонанса токов также равна нулю, а активная .

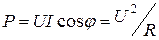Резонанс токов, как и резонанс напряжений, может быть достигнут изменением частоты, емкости или индуктивности. При этом резонансные величины определяются по формулам:

; ; .

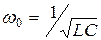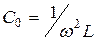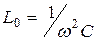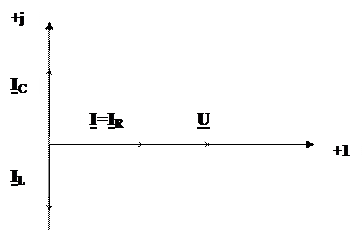На рис. 3.7 показана векторная диаграмма резонанса токов.

Рис. 3.7

Добротность контура в данном случае будет определять, во сколько раз токи на реактивных элементах превышают входной ток:

,

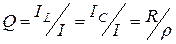где .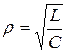

Дата добавления: 2014-01-06