Законы коммутации

ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ

ТЕМА

Электропривод

В современном автоматизированном производстве технологические процессы совершаются электромеханическими системами, состоящими из трех существенно различных частей: машины – двигателя, передаточного механизма и рабочей машины.

Первые две части: двигатель с системой управления и передаточный механизм (шкивы, муфты, редукторы) служат для передачи мощности и движения рабочей машине и объединяются под общим названием – привод.

Если в качестве двигателя используется электродвигатель, то привод называется электроприводом.

Кроме основных частей электропривода электродвигателя и передаточного механизма большая роль в его работе принадлежит аппаратуре управления (реле, контакторы) и преобразовательным устройствам (ионные преобразователи, преобразователи частоты).

Существует три основных типа электропривода:

1. Групповой (трансмиссионный), когда группа исполнительных механизмов приводится от одной или нескольких трансмиссий, которые вращает один двигатель. Этот тип электропривода неэкономичен и сегодня применяется редко.
2. В одиночном электроприводе один электродвигатель приводит в движение отдельную машину и исполнительный механизм, например металлорежущий станок. Отдельные механизмы этого станка приводятся от этого же двигателя через систему механических передач.
3. Многодвигательный электропривод характеризуется тем, что каждый отдельный механизм рабочей машины приводится своим электродвигателем.

Электромагнитные процессы в электрических цепях, происходящие при переходе от одного установившегося режима работы цепи к другому, отличному от предыдущего, называются переходными процессами. Они возникают в результате коммутации, а также при изменении параметров цепи, содержащей индуктивные и емкостные элементы.

Переходные процессы длятся доли секунд, однако токи и напряжения в это время могут достигать значений во много раз больших, чем при установившемся режиме. Это может привести к повреждениям отдельных участков цепи. Поэтому расчет переходных процессов имеет важное практическое значение.

Отсчет времени при анализе переходных процессов принято начинать от момента коммутации, в момент времени .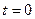

Первый закон коммутации:

ток через индуктивность не может измениться скачком:

,

где 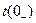– время непосредственно до коммутации;

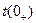– время непосредственно после коммутации.

Второй закон коммутации:

напряжение на емкости не может измениться скачком:

.

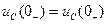Расчет переходных процессов в электрических цепях классическим методом

1. Составляют систему дифференциальных уравнений по законам Кирхгофа.

2. Записывают общее решение дифференциального уравнения в виде суммы частного решения неоднородного уравнения – установившийся (принужденный) режим и общего решения однородного уравнения – свободный процесс

или .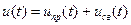

3. Рассчитывают принужденные (установившиеся) составляющие токов и напряжений от действия внешних источников ЭДС и источников тока.

4. При определении вида свободной составляющей переходных токов и напряжений составляют и решают характеристическое уравнение. Для этого записывают комплексное сопротивление цепи , заменяют 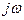на 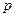и приравнивают к нулю. Решая уравнение , находят корни характеристического уравнения 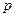. При одном корне свободные составляющие тока и напряжения имеет вид:

,

.

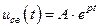5. Определяют постоянную интегрирования из начальных условий, т.е. при .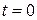

, ;

, .

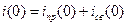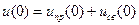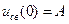Следует помнить, что корень характеристического уравнения 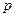всегда отрицателен, т.к. свободный процесс – процесс затухающий, он обусловлен запасом энергии в реактивных элементах электрической цепи.

При анализе переходных процессов вводят понятие постоянной времени цепи .

Пример. Последовательная 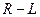цепь подключается к источнику постоянной ЭДС В (рис.6.6), Ом, 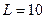мГн. Определить 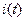и .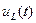

Рис.6.6.

Решение. Цепь содержит один реактивный элемент и описывается дифференциальным уравнением первой степени:

.

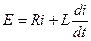Решение уравнения имеет вид .

Находим . В установившемся режиме индуктивность не оказывает сопротивления постоянному току, следовательно

А.

Составляем характеристическое уравнение и находим его корень:

,

,

.

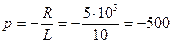Тогда

.

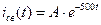Определяем из начальных условий:

.

По первому закону коммутации:

,

тогда при :

,

отсюда

.

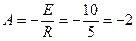Ток в цепи (рис.6.7).

Рис.6.7.

Напряжение на индуктивности (рис.6.8).

Рис.6.8.

Дата добавления: 2014-01-06