Исходные понятия математической логики

Лекция 1

1.1 Язык математической логики.

Основными понятиями математической логики являются высказывания, предикаты, логические связки и кванторы (мы не даем формального описания какого-либо языка, но несколько ниже мы приведём примеры таких языков для исчисления высказываний и исчисления предикатов). Сейчас же изложим семантические аспекты понятий выше. Связка Ø («не») называется отрицанием. Связка Ù (иначе &), («и») называется конъюнкцией. Связка Ú («или», но не разделительное) называется дизъюнкцией. Связка ® («если…,то…») называется импликацией. Приведём пример. Пусть Р – предложение «данное число делится на 2», Q – предложение «данное число делится на 5», R – предложение «данное число оканчивается нулём». Тогда предложение S «если данное число оканчивается нулём, то это число делится на 5 и делится на 2» может быть записано так: S = R ® (PÙQ). Читатель может потренироваться в приведении подобных примеров. Большое количество таких примеров имеется в начальной главе книги Э. Мендельсона «Введение в математическую логику».

Аналогом понятия предикат является понятие группы слов, характеризующих предмет, т.е. есть сказуемое, характеризующее подлежащее. Здесь часто используется так называемая функциональная запись: f(x₁, …,x_n), где f – обозначение свойства, которым характеризуется набор предметов x₁, …,x_n. С этой точки зрения предикат ставит в соответствие элементам x₁, …,x_n символы И (истина) или Л (ложь), которые далее всегда будут заменяться 1 и 0 соответственно. Итак, f: Mⁿ Þ {0, 1}, где М – объектная область, т.е. область, которую «пробегают» переменные x₁, …, x_n. Рассмотрим пример. Р(x) = «x – пионер» (это – одноместный предикат «быть пионером»). Если данное лицо А является пионером, то Р(А) = 1. В противном случае Р(А) = 0. В качестве М здесь выступает всё человечество. Другой пример. Q(x,y) = «x делится на y» (в качестве М выступает множество всех пар натуральных чисел). Теперь Q – двухместный предикат. Если А=28 и В=2, то Q(А,В)=1. Если же А=13, а В=4, то Q(А,В)=0. Если мы зафиксируем первую переменную числом 28, то получим предикат Q(28,y)=R(y) и R – уже одноместный предикат, выражающий делимость числа 28 на все остальные числа. Однако есть другой способ получения одних предикатов из других предикатов и такой способ связан с применением кванторов. Пусть P(x) и Q(x,y) – рассмотренные выше предикаты. Тогда "xP(x) («для всякого x из области М (М – всегда подразумеваемая область) Р(x)=1») и $yQ(x,y)=H(x) («для данного x из области М найдётся y из области М такой, что Q(x,y)=1») – новые предикаты (первый из них есть нульместный предикат или просто высказывание), полученные применением кванторов " (для всякого или всеобщности (for all)) и $ (существования (exist)) к предикатам P и Q. В первом случае мы получим функцию-константу или высказывание (в нашем случае – ложное), во втором случае – одноместный предикат, который всегда истинен (например, в качестве y нужно взять x), а тогда утверждение "x$yQ(x,y) – также истинное утверждение. Думается, что изложенного выше достаточно для уяснения понятия «квантор». Ниже, при изложении исчисления предикатов, мы вернёмся к этому понятию.

Перейдём теперь к более формальному изложению понятия «язык» в математической логике. При введении понятий «высказывание», «связка», «предикат» и «квантор» мы опирались на семантическую сторону или смысл (не точный, вообще говоря) этих понятий. Но теперь мы перейдём к более формальной стороне вопроса.

1.2 Высказывания и высказывательные формы.

Логические операции над высказываниями.

В пункте 1.1 мы уже получили представление о логических связках и кванторах. Теперь мы обратимся к высказываниям. Под высказыванием мы понимаем суждение, характеризующееся тем, что оно обязательно является либо истинным, либо ложным (последние слова – это истинностностные значения суждения или высказывания).

Высказывание 7´3=21 является истинным (его истинностное значение есть 1), а высказывание 7´7=47 – ложным (его истинностное значение есть 0). Однако бывают суждения, которые не являются высказываниями. Например, суждение «натуральное число n, умноженное на 5, всегда оканчивается (в десятичной записи) нулём» является неопределенным в том смысле, что его истинностное значение зависит от того, какое значение принимает натуральное число n, которое в данной записи носит характер переменной. Переменная n принимает значения из вполне определенного множества объектов: натуральных чисел и такая переменная называется «свободная». Но бывают и такие переменные, которые не допускают подстановок описанного рода. Например (сравни с действиями кванторов из примеров выше; ещё пример с кванторами: Ø$x(x²+1=0)). Такие переменные называют «связанная». Ещё пример связанной переменной: 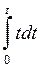. Здесь верхнее вхождение переменной t является свободным, а два других вхождения – связанными. Таким образом, нужно говорить не просто о свободных и связанных переменных, а об их вхождениях в суждение. Итак, наряду с высказываниями (в которых нет свободных вхождений ни одной переменной) существуют и суждения, в которых есть вхождения свободных переменных. Суждения такого вида называют высказывательными формами.

Вопрос. Какие примеры выше являются высказываниями, а какие – высказывательными формами? Является ли высказывание высказывательной формрой?

Обратимся теперь к введённым выше логическим операциям (связкам). К ним мы ещё добавим логическую операцию (бинарную) º («тогда и только тогда» или «эквиваленция»). Представим сводную логическую таблицу всех введённых операций.

  А В АÙВ АÚВ А®В АºВ ØА 1 1 1 1 1 1 0 1 0 0 1 0 0 0 0 1 0 1 1 0 1 0 0 0 0 1 1 1

Эти логические операции можно рассматривать как функции, например, Ù есть отображение из {0,1}² в {0,1}. Применять эти операции можно как к высказываниям, так и к высказывательным формам.

Дата добавления: 2014-01-06