
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Модели с дихотомическими (фиктивными) переменными
|
|
|
|
Эконометрический анализ при нарушении классических модельных предположений
4.1. Гетероскедастичность. Критерии Парка и Голдфелда – Квандта для обнаружения гетероскедастичности. При нахождении оценок коэффициентов эмпирических регрессий по наблюдениям 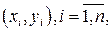 необходимо следить за выполнимостью предпосылок МНК, так как при их нарушении МНК может давать оценки с плохими статистическими свойствами. Одной из предпосылок МНК является условие постоянства дисперсий:
необходимо следить за выполнимостью предпосылок МНК, так как при их нарушении МНК может давать оценки с плохими статистическими свойствами. Одной из предпосылок МНК является условие постоянства дисперсий:
дисперсия случайной переменной 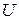 (случайных отклонений) должна быть одинакова и постоянна для всех
(случайных отклонений) должна быть одинакова и постоянна для всех 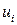 :
:  для любых наблюдений
для любых наблюдений 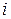 и
и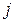 .
.
Это свойство возмущающей переменной 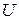 называется гомокедастичностью. Непостоянство дисперсии возмущающей переменной
называется гомокедастичностью. Непостоянство дисперсии возмущающей переменной 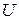 называется гетероскедастичностью.
называется гетероскедастичностью.
Данное условие подразумевает, что, несмотря на то, что при каждом конкретном наблюдении случайное отклонение может быть большим или маленьким, положительным или отрицательным, не может быть некой априорной причины, вызывающей большее отклонение при одних наблюдениях и меньшее – при других.
При невыполнимости данной предпосылки (при гетероскедастичности) последствия применения МНК могут быть следующими.
1. Оценки коэффициентов остаются несмещенными и линейными.
2. Оценки не будут эффективными (т.е. они не будут иметь наименьшую дисперсию по сравнению с другими оценками данного параметра). Они не будут и асимптотически эффективными. Увеличение дисперсии оценок снижает вероятность получения максимально точных оценок.
3. Дисперсии оценок будут рассчитываться со смещением, так как дисперсия 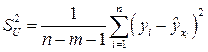 не является более несмещенной.
не является более несмещенной.
4. Вследствие вышесказанного все выводы, получаемые на основе соответствующих 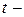 и
и 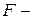 статистик, а также интервальные оценки будут ненадежными. Следовательно, статистические выводы, полученные при стандартных проверках значимости коэффициентов уравнения регрессии, могут быть ошибочными и приводить к неверным заключениям по построенной модели. Вполне вероятно, что стандартные ошибки коэффициентов будут занижены, а, следовательно,
статистик, а также интервальные оценки будут ненадежными. Следовательно, статистические выводы, полученные при стандартных проверках значимости коэффициентов уравнения регрессии, могут быть ошибочными и приводить к неверным заключениям по построенной модели. Вполне вероятно, что стандартные ошибки коэффициентов будут занижены, а, следовательно, 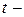 статистики будут завышены. Это может привести к признанию статистически значимыми коэффициентов, которые таковыми не являются.
статистики будут завышены. Это может привести к признанию статистически значимыми коэффициентов, которые таковыми не являются.
Для обнаружения гетероскедастичности применяются различные методы: графический анализ отклонений, критерии ранговой корреляции Спирмена, Парка, Глейзера, Голдфелда – Квандта.
Рассмотрим критерий Парка. Предположим, что дисперсия отклонений 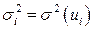 является функцией
является функцией 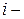 го значения
го значения 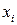 факторного признака, которая описывается функцией
факторного признака, которая описывается функцией 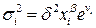 , где
, где 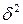 - неизвестная константа. Прологарифмировав эту функцию, получим
- неизвестная константа. Прологарифмировав эту функцию, получим 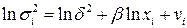 . Так как дисперсии
. Так как дисперсии  неизвестны, то их заменяют оценками квадратов отклонений
неизвестны, то их заменяют оценками квадратов отклонений 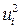 . Применение критерия Парка включает следующие шаги.
. Применение критерия Парка включает следующие шаги.
1. Строится уравнение регрессии 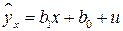 .
.
2. Для каждого наблюдения определяются 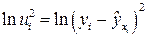 .
.
3. Строится регрессия
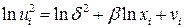 . (4.1)
. (4.1)
В случае множественной регрессии зависимость (4.1) строится для каждого факторного признака.
4. Проверяется статистическая значимость коэффициента 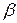 уравнения (4.1) при помощи статистики
уравнения (4.1) при помощи статистики  . Если коэффициент
. Если коэффициент 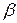 статистически значим, то это свидетельствует о наличии связи между
статистически значим, то это свидетельствует о наличии связи между 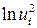 и
и 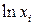 , т.е. о наличии гетероскедастичности в эмпирических данных.
, т.е. о наличии гетероскедастичности в эмпирических данных.
Критерий Голдфелда – Квандта. Предположим, что дисперсия отклонений 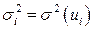 является функцией
является функцией 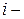 го значения
го значения 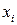 факторного признака, которая описывается функцией
факторного признака, которая описывается функцией 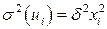 ,
, 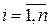 ; возмущающая переменная имеет нормальное распределение и отсутствует автокорреляция остатков
; возмущающая переменная имеет нормальное распределение и отсутствует автокорреляция остатков 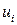 . Критерий Голдфелда – Квандта состоит в следующем:
. Критерий Голдфелда – Квандта состоит в следующем:
1. Все 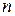 набдюдений упорядываются по величине значений фактора
набдюдений упорядываются по величине значений фактора 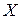 .
.
2. Упорядоченная выборка разбивается на три подвыборки объема 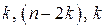 .
.
3. Строятся уравнения регрессии для первой и третьей подвыборок. Если предположение о пропорциональности дисперсий отклонений значениям 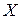 верно, то дисперсия регрессий по первой подвыборке,
верно, то дисперсия регрессий по первой подвыборке,  , будет существенно меньше дисперсии регрессии по третьей подвыборке,
, будет существенно меньше дисперсии регрессии по третьей подвыборке, 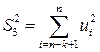 .
.
4. Для сравнения дисперсий составляется 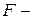 отношение:
отношение: 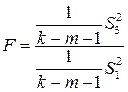 , которае подчиняется
, которае подчиняется 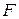 - распределению с числом степеней свободы
- распределению с числом степеней свободы 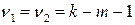 ,
, 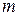 - количество факторных признаков в уравнении регрессии.
- количество факторных признаков в уравнении регрессии.
5. Если 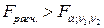 , то гипотеза об отсутствии гетороскедастичности отклоняется. В противном случае, т.е. если
, то гипотеза об отсутствии гетороскедастичности отклоняется. В противном случае, т.е. если 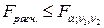 , нет оснований для отклонения гипотезы о гомоскедастичности остатков.
, нет оснований для отклонения гипотезы о гомоскедастичности остатков.
Голдфелд и Квандт для парной регрессии предлагают следующие размеры подвыборок: если 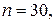 то
то 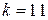 ; если
; если  , то
, то 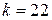 .
.
При множественной регрессии данный критерий применяется для факторного признака с найбольшей дисперсией  или для всех факторных признаков.
или для всех факторных признаков.
Критерий Голдфелда – Квандта можно применять и при обратной пропорциональной зависимости между  и значениями факторного признака.
и значениями факторного признака.
Пример 4.1. По эмпирическим данным, описывающих величину потребления ( , ден. ед.), в зависимости от величины дохода (
, ден. ед.), в зависимости от величины дохода (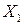 , ден. ед) и инвестиций (
, ден. ед) и инвестиций (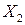 , ден.ед.):
, ден.ед.):

| |||||||
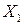
| |||||||
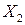
|
построить линейную регрессионную модель и проверить случайность остатков.
Р е ш е н и е. Линейная регрессионная модель зависимости объема потребления от величины дохода и инвестиций имеет вид:
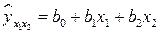 .
.
Коэффициенты 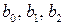 неизвестные величины. Определим их при помощи МНК. Применив ЭВМ, находим уравнение регрессии:
неизвестные величины. Определим их при помощи МНК. Применив ЭВМ, находим уравнение регрессии:
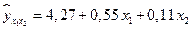 .
.
Подставив в полученное уравнение регрессии значения 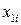 и
и  , вычисляем значения регрессии
, вычисляем значения регрессии 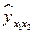 и остатки
и остатки 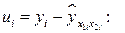
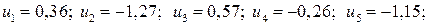
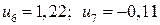 .
.
Случайность остатков проверим при помощи критерия серий. Для этого образуем последовательность из плюсов и минусов по следующему правилу: если 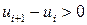 , то ставится плюс; если
, то ставится плюс; если 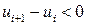 , то ставится минус. Для вычисленных остатков получаем следующую последовательность знаков:
, то ставится минус. Для вычисленных остатков получаем следующую последовательность знаков:
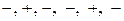 .
.
Общее число серий 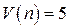 и протяженность самой длинной серии
и протяженность самой длинной серии  . Подставив эти значения в неравенства
. Подставив эти значения в неравенства 
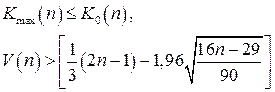 , получим 2 < 5, где
, получим 2 < 5, где 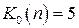 для
для 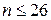 и 5 >
и 5 > 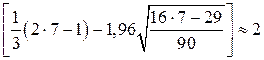 . Следовательно, отклонения от уравнения регрессии носят случайный характер.
. Следовательно, отклонения от уравнения регрессии носят случайный характер.
Проведем графический анализ зависимости остатков 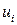 от теоретических значений результативного признака
от теоретических значений результативного признака 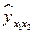 . Для этого построим на графике (рис. 4.1) значения отклонений. Поскольку точки находятся в полосе, обозначенной пунктирными линиями, то отклонения носят случайный характер и, следовательно, уравнение регрессии хорошо аппроксимирует изучаемое явление.
. Для этого построим на графике (рис. 4.1) значения отклонений. Поскольку точки находятся в полосе, обозначенной пунктирными линиями, то отклонения носят случайный характер и, следовательно, уравнение регрессии хорошо аппроксимирует изучаемое явление.

Рис 4.1
4.2. Методы смягчения проблемы гетероскедастичности. При установлении гетероскедастичности возникает необходимость преобразования модели с целью устранения этого недостатка. Вид преобразований зависит от того, известны или неизвестны дисперсии  отклонений
отклонений 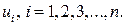
А). Если для каждого наблюдения известны значения  , то устранить гетероскедастичность можно, разделив каждое эмпирическое значение на соответствующее ему значение дисперсии и для преобразованных эмпирических данных можно применить метод наименьших квадратов при построении регрессии.
, то устранить гетероскедастичность можно, разделив каждое эмпирическое значение на соответствующее ему значение дисперсии и для преобразованных эмпирических данных можно применить метод наименьших квадратов при построении регрессии.
Рассмотрим парную линейную регрессию
 . (4.2)
. (4.2)
Разделим все члены уравнения на известное 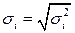 :
: 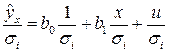 . Обозначив
. Обозначив 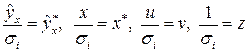 , получим уравнение регрессии
, получим уравнение регрессии 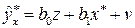 без свободного члена, но с дополнительным факторным признаком
без свободного члена, но с дополнительным факторным признаком 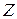 и с преобразованным отклонением
и с преобразованным отклонением 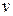 , для которого выполняется условие гомоскедастичнсти. Действительно,
, для которого выполняется условие гомоскедастичнсти. Действительно, 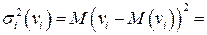
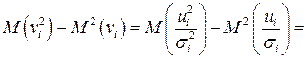

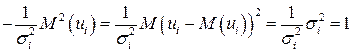 , так как
, так как 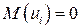 согласно первой предпосылке.
согласно первой предпосылке.
Рассмотренный метод преобразований называется взвешенным методом наименьших квадратов (ВМНК), который включает следующие шаги.
1. Значения каждой пары эмпирических данных 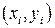 делят на известную величину
делят на известную величину 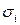 . Тем самым наблюдениям с наименьшими дисперсиями придаются большие «веса», чем наблюдениям с большими дисперсиями. При этом увеличивается вероятность получения более точных оценок.
. Тем самым наблюдениям с наименьшими дисперсиями придаются большие «веса», чем наблюдениям с большими дисперсиями. При этом увеличивается вероятность получения более точных оценок.
2. Для преобразованных значений 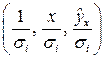 строится уравнение регрессии при помощи метода наименьших квадратов.
строится уравнение регрессии при помощи метода наименьших квадратов.
Б). Если фактические значения дисперсий  отклонений неизвестны, то формулируются различные предположения о дисперсиях:
отклонений неизвестны, то формулируются различные предположения о дисперсиях:
- дисперсии  пропорциональны
пропорциональны 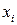 :
: 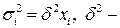 коэффициент пропорциональности. Тогда все члены уравнения (4.2) делим на
коэффициент пропорциональности. Тогда все члены уравнения (4.2) делим на 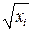 :
:
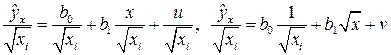 . (4.3)
. (4.3)
Можно показать, что для случайных отклонений 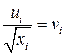 выполняется условие гомоскедастичности, Следовательно, для построения уравнения регрессии (4.3) можно применить МНК. Оценив коэффициенты
выполняется условие гомоскедастичности, Следовательно, для построения уравнения регрессии (4.3) можно применить МНК. Оценив коэффициенты 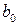 и
и 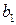 , возвращаемся к исходному уравнению регрессии (4.2).
, возвращаемся к исходному уравнению регрессии (4.2).
- дисперсии  пропорциональны
пропорциональны 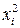 :
: 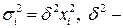 коэффициент пропорциональности. Соответствующим преобразованием будет деление всех членов уравнения (4.2) на
коэффициент пропорциональности. Соответствующим преобразованием будет деление всех членов уравнения (4.2) на 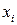 :
:
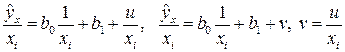 . (4.4)
. (4.4)
После определения оценок параметров 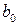 и
и 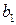 применяя МНК, возвращаемся к исходному уравнению регрессии (4.2).
применяя МНК, возвращаемся к исходному уравнению регрессии (4.2).
4.3. Автокорреляция остатков регрессионной модели. Критерий Дарбина – Уотсона. Другой важной предпосылкой МНК является предположение о попарной независимости значений случайных отклонений (остатков) 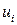 и
и 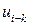 в вероятностном смысле, т.е.
в вероятностном смысле, т.е. 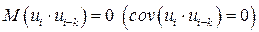 для
для 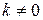 .
.
Корреляция между упорядоченными во времени или в пространстве последовательными или смещенными на лаг 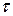 значениями одного и того же ряда наблюдений называется автокорреляцией.
значениями одного и того же ряда наблюдений называется автокорреляцией.
Автокорреляция остатков (отклонений) – это корреляция между последовательными значениями возмущающей переменной 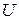 :
: 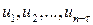 и
и 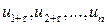 . Она обычно встречается в регрессионном анализе при изучении временных рядов. В экономических задачах значительно чаще встречается положительная автокорреляция (
. Она обычно встречается в регрессионном анализе при изучении временных рядов. В экономических задачах значительно чаще встречается положительная автокорреляция (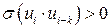 ), чем отрицательная автокорреляция (
), чем отрицательная автокорреляция (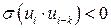 ). Положительная (отрицательная) автокорреляция вызывается постоянным направленным воздействием неучтенных в регрессионной модели факторами.
). Положительная (отрицательная) автокорреляция вызывается постоянным направленным воздействием неучтенных в регрессионной модели факторами.
Последствия автокорреляции в определенной мере сходны с последствиями гетороскедастичности, т.е. все выводы, получаемые на основе соответствующих 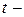 и
и 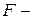 статистик, определяющих значимость коэффициентов регрессии и коэффициента детерминации, возможно, будут неверными. Вследствие этого ухудшаются прогнозные качества модели, поскольку оценки параметров уравнения регрессии, полученные с применением МНК, перестают быть эффективными.
статистик, определяющих значимость коэффициентов регрессии и коэффициента детерминации, возможно, будут неверными. Вследствие этого ухудшаются прогнозные качества модели, поскольку оценки параметров уравнения регрессии, полученные с применением МНК, перестают быть эффективными.
Для установления статистической независимости отклонений 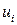 проверяется некоррелированность не любых, а только соседних величин
проверяется некоррелированность не любых, а только соседних величин 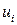 . Соседними значениями остатков
. Соседними значениями остатков 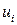 считаются соседние во времени или по возрастанию значений факторного признака
считаются соседние во времени или по возрастанию значений факторного признака 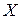 . Для анализа коррелированности этих величин коэффициент корреляции вычисляется по формуле:
. Для анализа коррелированности этих величин коэффициент корреляции вычисляется по формуле:
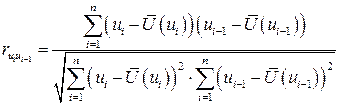 . (4.5)
. (4.5)
На практике, вместо коэффициента корреляции используют другие критерии. Наиболее распространенным критерием, позволяющим установить наличие автокорреляции остатков первого порядка, т.е. между соседними остаточными членами, является критерий Дарбина – Уотсона (см. п. 2.7).
При применении этого критерия формулируется основная гипотеза 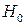 , состоящая в том, что автокорреляция остатков отсутствует:
, состоящая в том, что автокорреляция остатков отсутствует: 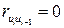 и альтернативная гипотеза
и альтернативная гипотеза 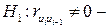 автокорреляция остатков существует. Для проверки выдвинутой гипотезы
автокорреляция остатков существует. Для проверки выдвинутой гипотезы 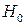 применяется статистика:
применяется статистика:
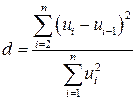 . (4.6)
. (4.6)
При больших значениях 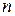 коэффициент корреляции и статистика
коэффициент корреляции и статистика 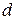 связаны равенством
связаны равенством
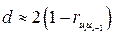 , (4.7)
, (4.7)
так как при больших значениях 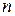 две суммы равны:
две суммы равны: 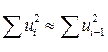 . Из равенства (4.7) следует, что если
. Из равенства (4.7) следует, что если 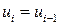 , то
, то  и
и 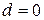 . Если
. Если 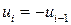 , то
, то 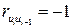 и
и 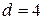 . Во всех других случаях
. Во всех других случаях 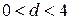 .
.
При случайном поведении отклонений (остатков) 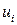 можно предположить, что в одной половине случаев знаки последовательных отклонений совпадают, а в другой – противоположны. Так как абсолютная величина отклонений в среднем предполагается одинаковой, то можно считать, что в половине случаев
можно предположить, что в одной половине случаев знаки последовательных отклонений совпадают, а в другой – противоположны. Так как абсолютная величина отклонений в среднем предполагается одинаковой, то можно считать, что в половине случаев 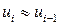 , а в другой
, а в другой 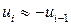 . Тогда
. Тогда
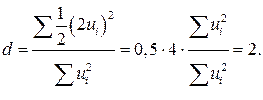
Таким образом, необходимым условием независимости случайных отклонений является близость к двойке значения статистики Дарбина – Уотсона. Следовательно, если 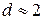 , то считаем отклонения от регрессии случайными (хотя в действительности они таковыми могут и не быть), а построенная эмпирическая линейная регрессия, вероятно, отражает реальную зависимость.
, то считаем отклонения от регрессии случайными (хотя в действительности они таковыми могут и не быть), а построенная эмпирическая линейная регрессия, вероятно, отражает реальную зависимость.
Для ответа на вопрос, какие значения статистики 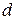 можно считать статистически близкими к двум, разработаны таблицы значений статистики Дарбина – Уотсона, позволяющие при данном числе наблюдений
можно считать статистически близкими к двум, разработаны таблицы значений статистики Дарбина – Уотсона, позволяющие при данном числе наблюдений 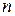 , количестве факторных признаков
, количестве факторных признаков 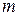 и заданном уровне значимости
и заданном уровне значимости 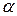 , определить границы области значений статистики
, определить границы области значений статистики 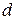 , при которых принимается или отклоняется гипотеза о наличии автокорреляции. Для заданных
, при которых принимается или отклоняется гипотеза о наличии автокорреляции. Для заданных 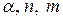 в таблице указываются два числа:
в таблице указываются два числа: 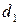 - нижняя граница и
- нижняя граница и  - верхняя граница. Выводы осуществляются по правилу:
- верхняя граница. Выводы осуществляются по правилу:
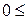
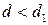 , существует положительная автокорреляция остатков;
, существует положительная автокорреляция остатков;
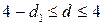 , существует отрицательная автокорреляция остатков;
, существует отрицательная автокорреляция остатков;
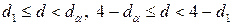 , вопрос о принятии или отвержении гипотезы о наличии автокорреляции остается открытым;
, вопрос о принятии или отвержении гипотезы о наличии автокорреляции остается открытым;
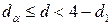 , автокорреляция отсутствует.
, автокорреляция отсутствует.
При грубой оценке считают, что если 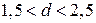 , то автокорреляция остатков отсутствует. Для более надежного вывода следует использовать таблицу. Отметим, что при наличии автокорреляции остатков построенное уравнение регрессии считается неудовлетворительным.
, то автокорреляция остатков отсутствует. Для более надежного вывода следует использовать таблицу. Отметим, что при наличии автокорреляции остатков построенное уравнение регрессии считается неудовлетворительным.
Применение статистики Дарбина – Уотсона основано на следующих предположениях:
1. Регрессионные модели должны содержать свободный член.
2. Случайные отклонения 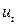 определяются по итерационной схеме
определяются по итерационной схеме 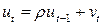 , называемой авторегрессионной схемой первого порядка.
, называемой авторегрессионной схемой первого порядка.
3. Эмпирические данные должны иметь одинаковую периодичность.
4. Критерий не применяется для авторегрессионных моделей.
При подтверждении автокорреляции остатков в первую очередь необходимо проанализировать спецификацию модели, т. е. уточнить состав факторных признаков, оказывающих влияние на результативный признак. Если после этого автокорреляция имеет место, то применяются различные преобразования модели, устраняющие автокорреляцию.
Для устранения автокорреляции можно воспользоваться авторегрессионной схемой первого порядка AR(1), применение которой рассмотрим на парной линейной регрессии
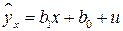 . (4.8)
. (4.8)
Тогда наблюдения 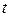 и
и 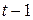 удовлетворяют таким же уравнениям:
удовлетворяют таким же уравнениям:
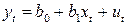 , (4.9)
, (4.9)
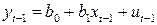 . (4.10)
. (4.10)
Предположим, что случайные отклонения описываются авторегрессионной моделью первого порядка:
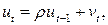 (4.11)
(4.11)
где 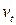 ,
, 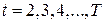 , - случайные отклонения, удовлетворяющие всем предпосылкам МНК,
, - случайные отклонения, удовлетворяющие всем предпосылкам МНК, 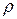 - коэффициент автокорреляции. Умножим соотношение (4.10) на
- коэффициент автокорреляции. Умножим соотношение (4.10) на 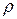 и вычтем из (4.9):
и вычтем из (4.9):
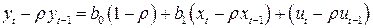 . (4.12)
. (4.12)
Введем обозначения 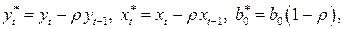 и учитывая (4.11), получим уравнение регрессии в виде:
и учитывая (4.11), получим уравнение регрессии в виде:
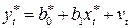 ,
,
коэффициенты 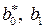 которого можно вычислить, применяя МНК. Коэффициенты
которого можно вычислить, применяя МНК. Коэффициенты 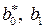 будут наилучшими оценками параметров уравнения регрессии изучаемой зависимости, так как случайные отклонения
будут наилучшими оценками параметров уравнения регрессии изучаемой зависимости, так как случайные отклонения 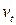 удовлетворяют предпосылкам МНК. При этом способе устранения автокорреляции происходит потеря первого наблюдения, что может привести к потере эффективности при малом числе наблюдений. Эта проблема обычно преодолевается с помощью поправки Прайса - Винстена:
удовлетворяют предпосылкам МНК. При этом способе устранения автокорреляции происходит потеря первого наблюдения, что может привести к потере эффективности при малом числе наблюдений. Эта проблема обычно преодолевается с помощью поправки Прайса - Винстена:
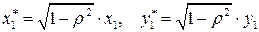 .
.
Если значение коэффициента автокорреляции 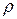 неизвестно, то в качестве его оценки можно взять коэффициент корреляции
неизвестно, то в качестве его оценки можно взять коэффициент корреляции 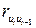 , вычисленный по формуле
, вычисленный по формуле 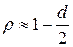 ,
, 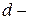 статистика Дарбина – Уотсона. Существуют и другие методы оценивания
статистика Дарбина – Уотсона. Существуют и другие методы оценивания 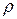 : методы Кохрана – Оркатта, Хилдретта – Лу.
: методы Кохрана – Оркатта, Хилдретта – Лу.
В случае, когда автокорреляция остатков велика, то применяется метод первых разностей. При этом методе уравнение регрессии (4.12), в котором полагаем 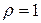 , преобразуется к виду:
, преобразуется к виду:
 ,
,
где 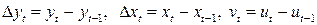 и коэффициент
и коэффициент 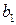 оценивается по МНК.
оценивается по МНК.
4.4. Мультиколлинеарность экзогенных переменных. Методы устранения мультиколлинеарности. Мультиколлинеарностью называется линейная зависимость между двумя или несколькими факторными признаками множественной линейной регрессии. Если факторные признаки связаны строгой линейной функциональной зависимостью, то мультиколлинеарность называется совершенной, а при существовании тесной корреляционной зависимости между факторными признаками – несовершенной. При существовании мультиколлинеарности могут возникнуть следующие последствия:
1. Большие стандартные ошибки оценок параметров уравнения регрессии, что приводит к увеличению интервальных оценок, ухудшению их точности.
2. Уменьшаются 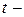 статистики коэффициентов, что может привести к неоправданному выводу о значимости влияния соответствующего фактора на результативный признак.
статистики коэффициентов, что может привести к неоправданному выводу о значимости влияния соответствующего фактора на результативный признак.
3. Становятся неустойчивыми оценки параметров уравнения регрессии при малейшем изменении данных.
4. Затрудняется определение вклада каждого из факторных признаков в объясняемую уравнением регрессии дисперсию результативного признака.
5. Возможно получение неверного знака у коэффициента регрессии.
Существует несколько признаков, по которым может быть установлена мультиколлинеорность.
1. Коэффициент детерминации 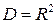 близок к единице, но некоторые из коэффициентов регрессии статистически незначимы, т. е. они имеют низкие
близок к единице, но некоторые из коэффициентов регрессии статистически незначимы, т. е. они имеют низкие 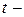 статистики.
статистики.
2. Между малозначимыми факторными признаками существует тесная корреляционная зависимость.
3.Тесная частная корреляционная зависимость между факторными признаками.
Мультиколлинеарность может иметь место, если какой – либо факторный признак связан тесной корреляционной зависимостью с другими факторными признаками. Для выявления этой зависимости строятся уравнения регрессии каждого факторного признака 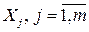 , на оставшиеся факторные признаки. Вычисляются соответствующие коэффициенты детерминации
, на оставшиеся факторные признаки. Вычисляются соответствующие коэффициенты детерминации 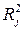 и оценивается их статистическая значимость на основе
и оценивается их статистическая значимость на основе 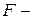 статистики:
статистики: 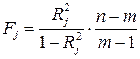 , где
, где 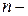 число наблюдений,
число наблюдений, 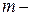 число факторных признаков в первоначальном уравнении регрессии. Статистика
число факторных признаков в первоначальном уравнении регрессии. Статистика 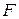 подчиняется распределению Фишера с числом степеней свободы
подчиняется распределению Фишера с числом степеней свободы 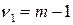 и
и  . Если коэффициент
. Если коэффициент 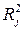 статистически значим, то есть основания считать, что между
статистически значим, то есть основания считать, что между 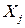 и другими факторными признаками существует корреляционная зависимость, следовательно, имеет место мультиколлинеарность. В противном случае, мультиколлинеарность отсутствует.
и другими факторными признаками существует корреляционная зависимость, следовательно, имеет место мультиколлинеарность. В противном случае, мультиколлинеарность отсутствует.
Прежде чем устранять мультиколлинеарность, определяется цель исследования. Если модель строится для прогнозирования, то при 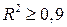 мультиколлинеарность не сказывается на прогнозных качествах модели. В других случаях, применяются методы для исключения мультиколлинеорности.
мультиколлинеарность не сказывается на прогнозных качествах модели. В других случаях, применяются методы для исключения мультиколлинеорности.
Простейшим методом устранения мультиколлинеарности является исключение из модели одной или ряда коррелированных переменных.
Для уменьшения мультиколлинеарности увеличивается объем выборки, что приводит к увеличению статистической значимости коэффициентов регрессии.
Изменяется форма модели, или добавляются факторные признаки, не учтенные в модели, но существенно влияющие на результативный признак (зависимую переменную). Это приводит к уменьшению стандартных ошибок коэффициентов регрессии.
Выполняются преобразования уравнения регрессии, путем деления на один из факторных признаков и др.
5.1. Необходимость использования фиктивных переменных. В регрессионных моделях в качестве факторных признаков часто приходится использовать не только количественные признаки, но и качественные. Например, спрос на продукцию может зависеть от вкусов потребителей, их национальных или религиозных особенностей и т. п.
Обычно в моделях влияние качественного фактора выражается в виде фиктивной (искусственной) переменной, которая отражает два противоположных состояния качественного фактора:
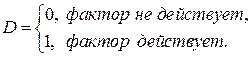
Переменная 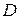 называется фиктивной (искусственной, двоичной) переменной (индикатором).
называется фиктивной (искусственной, двоичной) переменной (индикатором).
Таким образом, в регрессионном анализе рассматриваются модели, содержащие только количественные факторные признаки (обозначаемые 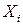 ), или качественные факторы (обозначаемые
), или качественные факторы (обозначаемые 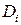 ), или те и другие одновременно.
), или те и другие одновременно.
Регрессионные модели, содержащие только качественные факторы, называются ANOVA – моделями (моделями дисперсионного анализа). Например, ANOVA - модель парной регрессии имеет вид:
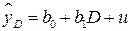 .
.
Очевидно, что условное математическое ожидание результативного признака равно:
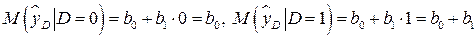 .
.
Следовательно, коэффициент 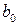 определяет среднее начальное значение результативного признака, коэффициент
определяет среднее начальное значение результативного признака, коэффициент 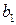 указывает, на какую величину отличается среднее начальное значение результативного признака при наличии или отсутствии качественного показателя. Проверяя статистическую значимость коэффициента
указывает, на какую величину отличается среднее начальное значение результативного признака при наличии или отсутствии качественного показателя. Проверяя статистическую значимость коэффициента 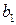 при помощи
при помощи 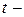 статистики, можно определить, влияет или нет фиктивный признак на результативный фактор.
статистики, можно определить, влияет или нет фиктивный признак на результативный фактор.
5.2. Регрессионные модели с количественными и качественными переменными. Модели, которые содержат количественные и качестенные факторные признаки, называются ANCOVA – моделями (моделями ковариационного анализа). Простейшая ANCOVA – модель с одним количественным и одним качественным признаками имеет вид:
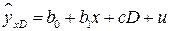 . (5.1)
. (5.1)
Ожидаемое значение результативного признака при альтернативных значениях фиктивного признака равно:
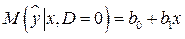 , (5.2)
, (5.2)
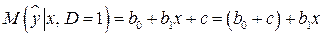 . (5.3)
. (5.3)
Из моделей (5.2) и (5.3) следует, что значение результативного признака изменяется с одним и тем же коэффициентом пропорциональности 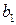 , отличаются лишь свободные члены на величину
, отличаются лишь свободные члены на величину 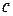 . Проверив при помощи
. Проверив при помощи 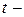 статистики статистические значимости коэффициентов
статистики статистические значимости коэффициентов 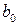 и
и 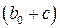 , можно определить влияние фиктивной переменной на результативный признак. При статистической значимости коэффициентов подтверждается влияние фиктивного фактора на результативный признак.
, можно определить влияние фиктивной переменной на результативный признак. При статистической значимости коэффициентов подтверждается влияние фиктивного фактора на результативный признак.
Значение фиктивного признака при 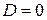 называется базовым или сравнительным. Коэффициент
называется базовым или сравнительным. Коэффициент 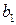 в модели (5.1) называется дифференциальным коэффициентом свободного члена, так как он показывает, на какую величину отличается свободный член модели при значении фиктивной переменной, равным единице, от свободного члена модели при базовом значении фиктивной переменной (при
в модели (5.1) называется дифференциальным коэффициентом свободного члена, так как он показывает, на какую величину отличается свободный член модели при значении фиктивной переменной, равным единице, от свободного члена модели при базовом значении фиктивной переменной (при 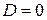 ).
).
В регрессионную модель можно вводить произвольное число качественных переменных. Например, регрессионная модель с двумя качественными признаками имеет вид:
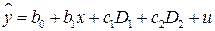 , (5.4)
, (5.4)
где
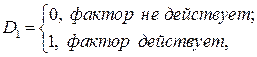
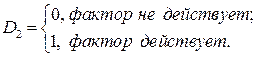
Из этой модели выводятся следующие регрессионные зависимости:
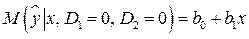 ,
,
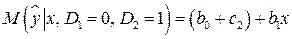 ,
,
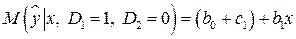 ,
,
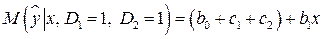 .
.
Регрессии отличаются лишь свободными членами. Дальнейшее определение статистической значимости коэффициентов 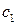 и
и 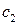 позволяет убедиться, влияют ли фиктивные факторы на результативный признак.
позволяет убедиться, влияют ли фиктивные факторы на результативный признак.
Описанные схемы могут быть распространены на регрессии с произвольным числом количественных и качественных факторов, при этом отметим, что если качественный фактор имеет 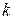 альтернативных состояний, то для его описания используется
альтернативных состояний, то для его описания используется 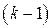 фиктивных переменных.
фиктивных переменных.
В рассмотренных выше случаях, предполагалось, что изменение значения качественного фактора влияет лишь на изменение свободного члена. Но существуют ситуации, когда изменение качественного фактора приводит к изменению, как свободного члена уравнения, так и коэффициента регрессии. Это характерно для временных рядов экономических данных при изменении институциональных условий, введении новых правовых или налоговых ограничений. В этом случае уравнение регрессии будет иметь вид:
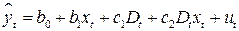 , (5.5)
, (5.5)
где
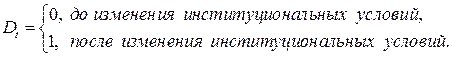
Ожидаемые значения результативного признака определяются уравнениями:
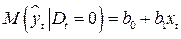 , (5.6)
, (5.6)

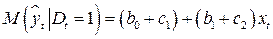 . (5.7)
. (5.7)
Коэффициенты 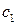 и
и 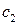 в уравнении (5.5) называются дифференциальным свободным членом и дифференциальным угловым коэффициентом соответственно. Фиктивный фактор
в уравнении (5.5) называются дифференциальным свободным членом и дифференциальным угловым коэффициентом соответственно. Фиктивный фактор 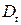 в уравнении регрессии (5.5) используется как в аддитивном виде
в уравнении регрессии (5.5) используется как в аддитивном виде 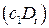 , так и в мультипликативном
, так и в мультипликативном 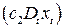 , что позволяет разбивать уравнение регрессии на два уравнения, связанные с периодами изменения рассматриваемого в модели качественного фактора.
, что позволяет разбивать уравнение регрессии на два уравнения, связанные с периодами изменения рассматриваемого в модели качественного фактора.
Для ответа на вопрос, можно ли за весь рассматриваемый период времени строить единое уравнение регрессии, или же нужно разбить временной интервал на части и на каждой из них строить свое уравнение регрессии, используется тест Чоу. Применение теста Чоу состоит в следующем.
1. Строится уравнение регрессии по выборке объема 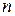 и вычисляется сумма квадратов отклонений значений
и вычисляется сумма квадратов отклонений значений 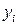 от общего уравнения регрессии:
от общего уравнения регрессии: 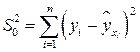 .
.
2. Выборку разбиваем на две подвыборки объемами 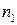 и
и 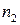 соответственно
соответственно 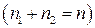 .
.
3. Для каждой из подвыборок строим уравнения регрессий и вычисляем суммы квадратов отклонений 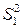 и
и 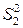 значений
значений 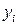 , для каждой из подвыборок, от соответствующих уравнений регрессий.
, для каждой из подвыборок, от соответствующих уравнений регрессий.
4. Проводим сравнение дисперсий на основе 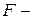 статистики:
статистики:
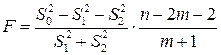 ,
,
имеющей распределение Фишера с числом степеней свободы 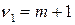 и
и  , где
, где 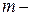 число факторных признаков во всех трех уравнениях регрессий.
число факторных признаков во всех трех уравнениях регрессий. 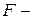 статистика близка к нулю, если
статистика близка к нулю, если 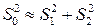 . Тогда
. Тогда 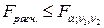 и это означает, что нет смысла разбивать уравнение регрессии на части. Если же
и это означает, что нет смысла разбивать уравнение регрессии на части. Если же 
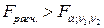 , то это означает необходимость введения в уравнение регрессии фиктивной переменной, т.е. целесообразность разбиения на подвыборки с точки зрения улучшения качества модели.
, то это означает необходимость введения в уравнение регрессии фиктивной переменной, т.е. целесообразность разбиения на подвыборки с точки зрения улучшения качества модели.
5.3. Модели с фиктивными результативными признаками. Рассмотрим модели с фиктивными результативными признаками, факторные признаки которых могут быть как количественными, так и качественными. Например, при анализе наличия работы у гражданина в зависимости от возраста, образования, семейного положения, доходов остальных членов семьи и т.д., то в качестве результативного признака выступает фиктивная переменная:
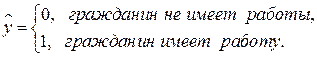
Указанные модели представимы в виде:
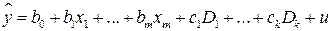 . (5.8)
. (5.8)
Модели (5.8) называются линейными вероятностными моделями (LPM – моделями).
Предположим, что зависимость фиктивного результативного признака и количественного факторного признака описывается уравнением регрессии:
 . (5.9)
. (5.9)
Из уравнения (5.9) следует, что среднее ожидаемое значение 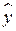 при
при 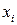 , с учетом того, что
, с учетом того, что 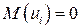 , определяется соотношением
, определяется соотношением 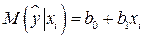 . По определению математического ожидания,
. По определению математического ожидания, 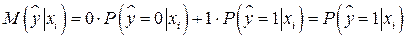 . Следовательно,
. Следовательно,
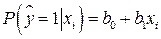 .
.
Так как 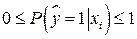 , то получено противоречие с определением вероятности. Это противоречие и другие ограничения применения МНК устраняются применением logit моделей.
, то получено противоречие с определением вероятности. Это противоречие и другие ограничения применения МНК устраняются применением logit моделей.
Поскольку использование LPM моделей имеет определенные ограничения, то применяются logit модели, в которых вероятности 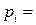
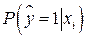 представляются в виде:
представляются в виде: 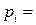
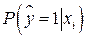 =
=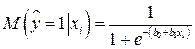 и рассматривается логарифм отношения вероятностей
и рассматривается логарифм отношения вероятностей
 ,
,
выражаемый линейной функцией. Для определения коэффициентов 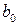 и
и 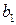 применяется взвешенный метод наименьших квадратов. При этом предварительно определяются значения
применяется взвешенный метод наименьших квадратов. При этом предварительно определяются значения 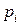 , используя эмпирические данные. Если эмпирические данные описываются выборкой сгруппированных данных, то в качестве вероятностей
, используя эмпирические данные. Если эмпирические данные описываются выборкой сгруппированных данных, то в качестве вероятностей 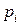 можно использовать их оценки – относительные частоты
можно использовать их оценки – относительные частоты 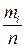 . При несгруппированных данных для нахождения оценок вероятностей
. При несгруппированных данных для нахождения оценок вероятностей 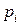 используется метод максимального правдоподобия.
используется метод максимального правдоподобия.
|
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 959; Нарушение авторских прав?; Мы поможем в написании вашей работы!