
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Введение. Ивановский государственный энергетический университет
|
|
|
|
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА

Ивановский государственный энергетический университет
Электромеханический факультет
Кафедра теоретической и прикладной механики
Автор: к.т.н., доцент М.А. Ноздрин
Теоретическая механика является одной из важнейших фундаментальных общенаучных дисциплин. Она играет существенную роль в подготовке инженеров любых специальностей. На результатах теоретической механики базируются общеинженерные дисциплины: сопротивление материалов, детали машин, теория механизмов и машин и другие.
Основной задачей теоретической механики является изучение движения материальных тел под действием сил. Важной частной задачей представляется изучение равновесия тел под действием сил.
Литература, рекомендуемая для изучения курса
- Добронравов В.В., Никитин Н.Н. Курс теоретической механики. М., Высшая школа, 1983.
- Бутенин Н.В., Лунц Я.Л., Меркин Д.Р. Курс теоретической механики, ч.1 и 2. М., Высшая школа, 1971.
- Петкевич В.В. Теоретическая механика. М., Наука, 1981.
- Сборник заданий для курсовых работ по теоретической механике. Под ред. А.А.Яблонского. М., Высшая школа, 1985.
| Навигация / Теория / 1. Структура теоретической механики. Основы статики |
В теоретической механике изучается движение тел относительно других тел, представляющие собой физические системы отсчёта.
Механика позволяет не только описывать, но и предсказывать движение тел, устанавливая причинные связи в определённом, весьма широком, круге явлений.
Основные абстрактные модели реальных тел:
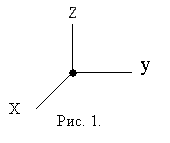 Время – в классической (нерелятивистской) механике абсолютно, единое для всех систем отсчёта то есть начальный момент – произволен. В отличие релятивистской механики, где применяется принцип относительности.
Состояние движения системы в момент времени t определяется координатами и скоростями точек в этот момент.
Реальные тела взаимодействуют при этом возникают силы, которые меняют состояние движения системы. Это и есть суть теоретической механики.
Как изучается теоретическая механика? Время – в классической (нерелятивистской) механике абсолютно, единое для всех систем отсчёта то есть начальный момент – произволен. В отличие релятивистской механики, где применяется принцип относительности.
Состояние движения системы в момент времени t определяется координатами и скоростями точек в этот момент.
Реальные тела взаимодействуют при этом возникают силы, которые меняют состояние движения системы. Это и есть суть теоретической механики.
Как изучается теоретическая механика?
 Рис.2.
Следствие. Силы, приложенные к точке твёрдого тела, складываются по правилу параллелограмма.
Аксиома 2. Две силы, приложенные к твёрдому телу, взаимно уравновешиваются тогда и только тогда, когда они равны по величине, направлены в противоположные стороны и лежат на одной прямой.
Аксиома 3. Действие на твёрдое тело системы сил не изменится, если добавить к этой системе или отбросить от неё две силы, равные по величине, направленные в противоположные стороны и лежащие на одной прямой.
Следствие. Силу, действующую на точку твёрдого тела, можно переносить вдоль линии действия силы без изменения равновесия (то есть, сила является скользящим вектором, рис.3)
Рис.2.
Следствие. Силы, приложенные к точке твёрдого тела, складываются по правилу параллелограмма.
Аксиома 2. Две силы, приложенные к твёрдому телу, взаимно уравновешиваются тогда и только тогда, когда они равны по величине, направлены в противоположные стороны и лежат на одной прямой.
Аксиома 3. Действие на твёрдое тело системы сил не изменится, если добавить к этой системе или отбросить от неё две силы, равные по величине, направленные в противоположные стороны и лежащие на одной прямой.
Следствие. Силу, действующую на точку твёрдого тела, можно переносить вдоль линии действия силы без изменения равновесия (то есть, сила является скользящим вектором, рис.3)
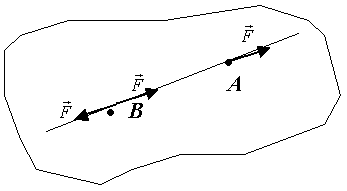 Рис.3.
Две категории сил.
1) Активные – создают или способны создать движение твёрдого тела. Например, сила веса.
2) Пассивные – не создающие движения, но ограничивающие перемещения твёрдого тела, препятствующие перемещениям. Например, сила натяжения нерастяжимой нити (рис.4).
Рис.3.
Две категории сил.
1) Активные – создают или способны создать движение твёрдого тела. Например, сила веса.
2) Пассивные – не создающие движения, но ограничивающие перемещения твёрдого тела, препятствующие перемещениям. Например, сила натяжения нерастяжимой нити (рис.4).
 Рис.4.
Аксиома 4. Действие одного тела на второе равно и противоположно действию этого второго тела на первое (действие равно противодействию).
Геометрические условия, ограничивающие перемещение точек, будем называть связями.
Условия связи: например,
Рис.4.
Аксиома 4. Действие одного тела на второе равно и противоположно действию этого второго тела на первое (действие равно противодействию).
Геометрические условия, ограничивающие перемещение точек, будем называть связями.
Условия связи: например,
 - стержень непрямой длины l. - стержень непрямой длины l.
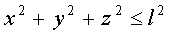 - гибкая нерастяжимая нить длиной l.
Силы, обусловленные связями и препятствующие перемещениям, называются силами реакций.
Аксиома 5. Связи, наложенные на систему материальных точек, можно заменить силами реакций, действие которых эквивалентно действию связей.
Когда пассивные силы не могут уравновесить действие активных сил, начинается движение.
Две частные задачи статики
1. Система сходящихся сил, действующих на твёрдое тело
Системой сходящихся сил называется такая система сил, линии действия которой пересекаются в одной точке, которую всегда можно принять за начало координат (рис.5). - гибкая нерастяжимая нить длиной l.
Силы, обусловленные связями и препятствующие перемещениям, называются силами реакций.
Аксиома 5. Связи, наложенные на систему материальных точек, можно заменить силами реакций, действие которых эквивалентно действию связей.
Когда пассивные силы не могут уравновесить действие активных сил, начинается движение.
Две частные задачи статики
1. Система сходящихся сил, действующих на твёрдое тело
Системой сходящихся сил называется такая система сил, линии действия которой пересекаются в одной точке, которую всегда можно принять за начало координат (рис.5).
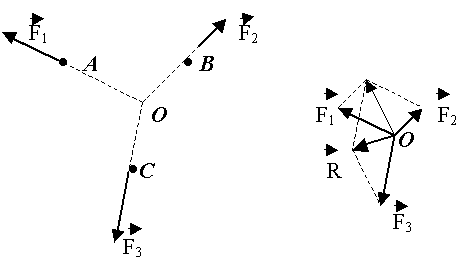 Рис.5.
Проекции равнодействующей:
Рис.5.
Проекции равнодействующей:
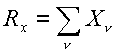 ; ;
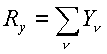 ; ;
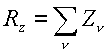 .
Если .
Если  , то сила вызывает движение твёрдого тела.
Условие равновесия для сходящейся системы сил: , то сила вызывает движение твёрдого тела.
Условие равновесия для сходящейся системы сил:
2. Равновесие трёх сил
Рис.6. Если на твёрдое тело действуют три силы, и линии действия двух сил пересекаются в некоторой точке А, равновесие возможно тогда и только тогда, когда линия действия третьей силы тоже проходит через точку А, а сама сила Примеры:
Рис.9.
Момент силы Итак:
где
Рис.10.
Моментом силы Это скаляр, не зависящий от выбора точки. Действительно, разложим О моментах: пусть О1 – точка пересечения а) от б) от Итак, момент относительно оси – это момент составляющей силы в перпендикулярной плоскости к оси относительно точки пересечения плоскости и оси. Теорема Вариньона для системы сходящихся сил: Момент равнодействующей силы для системы сходящихся сил относительно произвольной точки А равен сумме моментов всех составляющих сил относительно той же точки А (рис.11).
Рис.11.
Доказательство в теории сходящихся векторов. Пояснение: сложение сил по правилу параллелограмма => результирующая сила даёт суммарный момент.
Контрольные вопросы: 1. Назовите основные модели реальных тел в теоретической механике. 2. Сформулируйте аксиомы статики. 3. Что называется моментом силы относительно точки? | |||||||||||||
| Условия равновесия произвольной системы сил |
Из основных аксиом статики следуют элементарные операции над силами:
1) силу можно переносить вдоль линии действия;
2) силы, линии действия которых пересекаются, можно складывать по правилу параллелограмма (по правилу сложения векторов);
3) к системе сил, действующих на твёрдое тело, можно всегда добавить две силы, равные по величине, лежащие на одной прямой и направленные в противоположные стороны.
Элементарные операции не изменяют механического состояния системы.
Назовём две системы сил эквивалентными, если одна из другой может быть получена с помощью элементарных операций (как в теории скользящих векторов).
Система двух параллельных сил, равных по величине и направленных в противоположные стороны, называется парой сил (рис.12).
 Момент пары сил
Момент пары сил 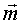 - вектор, по величине равный площади параллелограмма, построенного на векторах пары, и направленный ортогонально к плоскости пары в ту сторону, откуда вращение, сообщаемое векторами пары, видно происходящим против хода часовой стрелки. - вектор, по величине равный площади параллелограмма, построенного на векторах пары, и направленный ортогонально к плоскости пары в ту сторону, откуда вращение, сообщаемое векторами пары, видно происходящим против хода часовой стрелки.
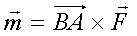 , то есть момент силы , то есть момент силы 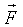 относительно точки В.
Пара сил полностью характеризуется своим моментом.
Пару сил можно переносить элементарными операциями в любую плоскость, параллельную плоскости пары; изменять величины сил пары обратно пропорционально плечам пары.
Пары сил можно складывать, при этом моменты пар сил складываются по правилу сложения (свободных) векторов.
Приведение системы сил, действующих на твёрдое тело, к произвольной точке (центру приведения) - означает замену действующей системы более простой: системой трёх сил, одна из которых проходит через наперёд заданную точку, а две другие представляют пару.
Доказывается с помощью элементарных операций (рис.13). относительно точки В.
Пара сил полностью характеризуется своим моментом.
Пару сил можно переносить элементарными операциями в любую плоскость, параллельную плоскости пары; изменять величины сил пары обратно пропорционально плечам пары.
Пары сил можно складывать, при этом моменты пар сил складываются по правилу сложения (свободных) векторов.
Приведение системы сил, действующих на твёрдое тело, к произвольной точке (центру приведения) - означает замену действующей системы более простой: системой трёх сил, одна из которых проходит через наперёд заданную точку, а две другие представляют пару.
Доказывается с помощью элементарных операций (рис.13).
 Рис.13.
Рис.13.
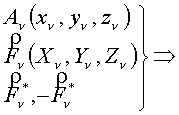 Система сходящихся сил Система сходящихся сил  и система пар сил и система пар сил  . .
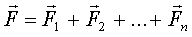 - результирующая сила - результирующая сила 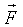 . .
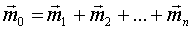 - результирующая пара - результирующая пара  .
Что и требовалось показать.
Две системы сил будут эквивалентны тогда и только тогда, когда обе системы приводятся к одной результирующей силе и одной результирующей паре, то есть при выполнении условий: .
Что и требовалось показать.
Две системы сил будут эквивалентны тогда и только тогда, когда обе системы приводятся к одной результирующей силе и одной результирующей паре, то есть при выполнении условий:
Общий случай равновесия системы сил, действующих на твёрдое тело
Рис.14.
Приведём систему сил к (рис.14):
То есть привели к Равновесие, если Тогда Далее:
Итак, общие условия равновесия твёрдого тела:
Эти условия справедливы для произвольной точки пространства.
Контрольные вопросы: 1. Перечислите элементарные операции над силами. 2. Какие системы сил называются эквивалентными? 3. Напишите общие условия равновесия твёрдого тела. | ||
| равнения равновесия твёрдого тела |
Пусть О – начало координат; 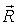 – результирующая сила; – результирующая сила; 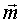 – момент результирующей пары. Пусть точка О1 – новый центр приведения (рис.15). – момент результирующей пары. Пусть точка О1 – новый центр приведения (рис.15).
 Рис.15.
Рис.15.
 и и 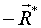 : : 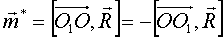 .
Новая система сил: .
Новая система сил:
 Заметим:
Заметим:
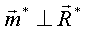 . .
 При изменении точки приведения => меняется только
При изменении точки приведения => меняется только 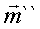 (в одну сторону с одним знаком, в другую – с другим). То есть (в одну сторону с одним знаком, в другую – с другим). То есть  точка: точка:  совпадают линии совпадают линии  и и 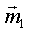 Аналитически:
Аналитически:  (колинеарность векторов)
Или: (колинеарность векторов)
Или: 
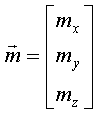 ; ; 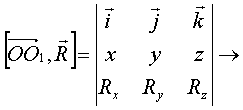 координаты точки О1. координаты точки О1.
 Рис.16.
Рис.16.
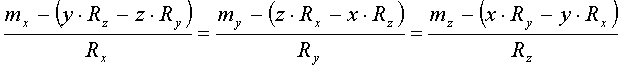 Это уравнение прямой линии, для всех точек которой направление результирующего вектора совпадает с направлением момента результирующей пары – прямая называется динамой.
Если на оси динамы =>
Это уравнение прямой линии, для всех точек которой направление результирующего вектора совпадает с направлением момента результирующей пары – прямая называется динамой.
Если на оси динамы =>  , то система эквивалентна одной результирующей силе, которую называют равнодействующей силой системы. При этом всегда , то система эквивалентна одной результирующей силе, которую называют равнодействующей силой системы. При этом всегда  , то есть , то есть 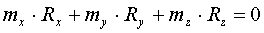 .
Четыре случая приведения сил:
1.) .
Четыре случая приведения сил:
1.)  ; ;  - динама.
2.) - динама.
2.)  ; ;  - равнодействующая.
3.) - равнодействующая.
3.)  ; ;  - пара.
4.) - пара.
4.)  ; ;  - равновесие.
Два векторных уравнения равновесия: главный вектор и главный момент равны нулю - равновесие.
Два векторных уравнения равновесия: главный вектор и главный момент равны нулю  , , 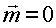 .
Или шесть скалярных уравнений в проекциях на декартовые оси координат: .
Или шесть скалярных уравнений в проекциях на декартовые оси координат:
 Здесь:
Здесь: 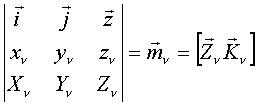 Сложность вида уравнений зависит от выбора точки приведения => искусство расчётчика.
Нахождение условий равновесия системы твёрдых тел, находящихся во взаимодействии <=> задача о равновесии каждого тела в отдельности, причём на тело действуют внешние силы и силы внутренние (взаимодействие тел в точках соприкосновения с равными и противоположно направленными силами – аксиома IV, рис.17).
Сложность вида уравнений зависит от выбора точки приведения => искусство расчётчика.
Нахождение условий равновесия системы твёрдых тел, находящихся во взаимодействии <=> задача о равновесии каждого тела в отдельности, причём на тело действуют внешние силы и силы внутренние (взаимодействие тел в точках соприкосновения с равными и противоположно направленными силами – аксиома IV, рис.17).
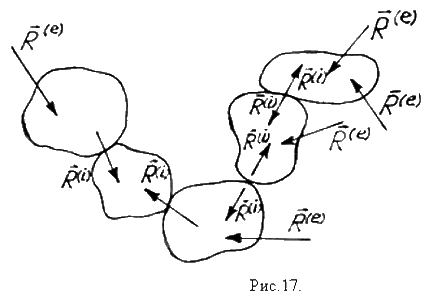 Выберем для всех тел системы один центр приведения. Тогда для каждого тела с номером
Выберем для всех тел системы один центр приведения. Тогда для каждого тела с номером  условия равновесия: условия равновесия:
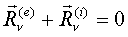 , ,  , ( , ( = 1, 2, …, k)
где = 1, 2, …, k)
где 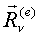 , ,  - результирующая сила и момент результирующей пары всех сил, кроме внутренних реакций. - результирующая сила и момент результирующей пары всех сил, кроме внутренних реакций.
 , ,  - результирующая сила и момент результирующей пары сил внутренних реакций.
Формально суммируя по - результирующая сила и момент результирующей пары сил внутренних реакций.
Формально суммируя по  и учитывая по IV аксиоме и учитывая по IV аксиоме
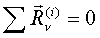
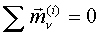 получаем необходимые условия равновесия твёрдого тела:
получаем необходимые условия равновесия твёрдого тела:
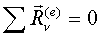 , , 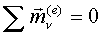 Пример.
Равновесие:
Пример.
Равновесие:  =? =?
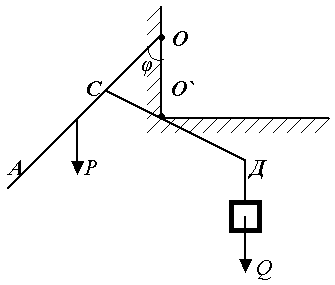 Рис.18.
Контрольные вопросы:
1. Назовите все случаи приведения системы сил к одной точке.
2. Что такое динама?
3. Сформулируйте необходимые условия равновесия системы твёрдых тел.
Рис.18.
Контрольные вопросы:
1. Назовите все случаи приведения системы сил к одной точке.
2. Что такое динама?
3. Сформулируйте необходимые условия равновесия системы твёрдых тел.
|
| 4. Плоская система сил |
Частный случай общей поставки задачи.
Пусть все действующие силы лежат в одной плоскости – например, листа. Выберем за центр приведения точку О – в этой же плоскости. Получим результирующую силу 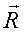 и результирующую пару и результирующую пару  в этой же плоскости, то есть в этой же плоскости, то есть  (рис.19) (рис.19)
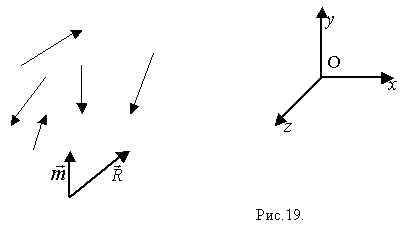 Замечание.
Систему можно привести к одной результирующей силе.
Условия равновесия:
Замечание.
Систему можно привести к одной результирующей силе.
Условия равновесия:
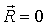 , ,  или скалярные:
или скалярные:
 Очень часто встречаются в приложениях, например, в сопротивлении материалов.
Пример.
Очень часто встречаются в приложениях, например, в сопротивлении материалов.
Пример.
 С трением шара о доску и о плоскость. Условие равновесия:
С трением шара о доску и о плоскость. Условие равновесия:  =?
Задача о равновесии несвободного твёрдого тела.
Несвободным называется такое твёрдое тело, перемещение которого стеснено связями. Например, другими телами, шарнирными закреплениями.
При определении условий равновесия: несвободное тело можно рассматривать как свободное, заменяя связи неизвестными силами реакции.
Пример. =?
Задача о равновесии несвободного твёрдого тела.
Несвободным называется такое твёрдое тело, перемещение которого стеснено связями. Например, другими телами, шарнирными закреплениями.
При определении условий равновесия: несвободное тело можно рассматривать как свободное, заменяя связи неизвестными силами реакции.
Пример.
 Контрольные вопросы:
1. Что называется плоской системой сил?
2. Напишите условия равновесия плоской системы сил.
3. Какое твёрдое тело называется несвободным?
Контрольные вопросы:
1. Что называется плоской системой сил?
2. Напишите условия равновесия плоской системы сил.
3. Какое твёрдое тело называется несвободным?
|
| 5. Частные случаи равновесия твёрдого тела |
Теорема. Три силы уравновешивают твёрдое тело только в том случае, когда все они лежат в одной плоскости.
Доказательство. Выберем за точку приведения точку на линии действия третьей силы. Тогда
Рис.22.
То есть плоскости
Условия равновесия твёрдого тела с одной неподвижной точкой. Центр приведения – закреплённая точка (рис.23):
Рис.23.
Моменты (условия равновесия):
Для определения реакций => результирующая:
Условия равновесия твёрдого тела, способного вращаться вокруг неподвижной оси.
Рис.24.
Закреплены две точки О и О1. Центр приведения: точка О (рис.24).
Уравнения равновесия:
Положение тела в пространстве определяется одним параметром, например, углом поворота
Условия равновесия твёрдого тела, способного перемещаться параллельно неподвижной плоскости (рис.25).
Рис.25.
Уравнения равновесия:
где Два первых и последнее уравнения – необходимые условия равновесия. Три остальных => реакции, то есть только для закрепления в трёх точках. Иначе => статически неопределимая задача.
Случай опоры на три точки. Для определения реакций имеем:
где
Решение имеется только при условии:
то есть три точки опоры не лежат на одной прямой. Иначе, статическая неопределимость.
Пример.
Рис.26.
Если дано, что опора упругая =>
Тогда для реакции: (удобно взять начало координат в одной из опор).
Контрольные вопросы: 1. В каком случае три силы уравновешивают твёрдое тело? 2. Как выглядят условия равновесия тела с одной неподвижной точкой? 3. Напишите уравнения равновесия тела, способного вращаться вокруг неподвижной оси. | ||||||
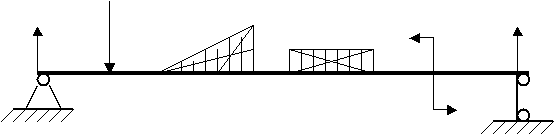
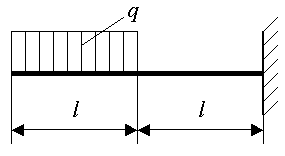
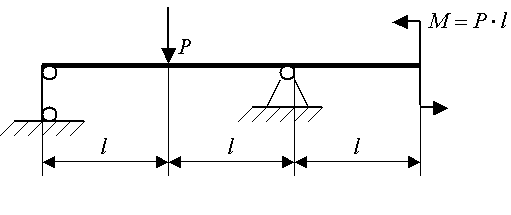
| 6. Задача о равновесии бруса |
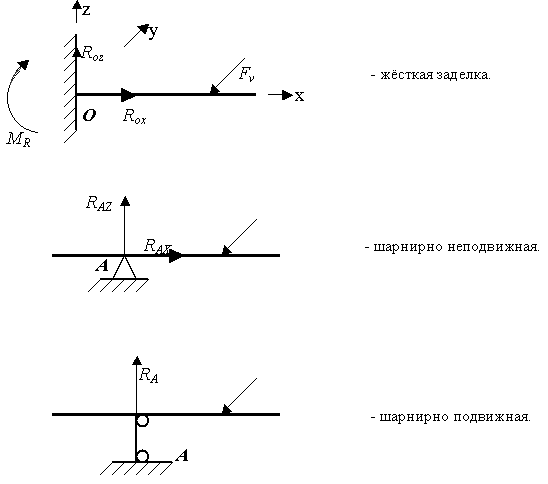
Виды опор:
Рис.27. Уравнения равновесия:
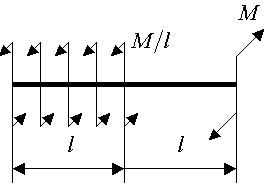
Виды нагрузок:
Рис.28. Найти: RA, RB.
Проверка:
Контрольные вопросы: 1. Назовите виды опор в???????? схемах. 2. Чем отличаются шарнирно подвижная и шарнирно неподвижная опоры? 3. Какие уравнения являются наиболее удобными для нахождения реакций в брусе? | |||
| 7. Определение внутренних усилий в стержневых конструкциях |
Внутренние усилия определяются методом сечений (РОЗУ), состоящим из четырёх этапов:
Р – рассекаем, то есть проводим сечение в том месте, где определяются внутренние усилия;
О – отбрасываем одну из частей и рассматриваем оставшуюся часть;
З – заменяем действие отброшенной части на рассматриваемую внутренними усилиями, которые приводим к центру тяжести сечения. Проецируя приведённые усилия на оси, получаем следующие неизвестные:
N – продольная сила;
Qy, Qz – поперечные силы;
Мкр – крутящий момент;
My, Mz – изгибающие моменты.
Эти усилия направляются в соответствии с правилами статики для выбранной системы координат:
Рис.29. У – уравновешиваем, то есть составляем шесть уравнений равновесия, из которых и определяются внутренние усилия. Затем строятся графики внутренних усилий вдоль оси бруса, которые называются эпюрами внутренних усилий.
Частные случаи. 1) Изгиб (Qz, My).
2) Изгиб (Qz, My).
3) Растяжение, сжатие (N).
4) Кручение (Мкр).
Рис.30. Контрольные вопросы: 1. Из каких этапов состоит метод сечений? 2. Что называется эпюрой внутреннего усилия? 3. Перечислите основные частные случаи нагружения бруса. | ||
| 8. Основы кинематики точки |
Кинематикой называется та часть механики, в которой изучаются зависимости между величинами, характеризующими состояние систем, но не рассматриваются причины вызывающие изменение состояние движения.
Кинематика точки. Декартовы координаты.
С неподвижной системой отсчёта связываем декартовую ортогональную систему координат (правую, рис. 31).
 Рис.31.
Точка
Рис.31.
Точка 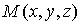 , где , где
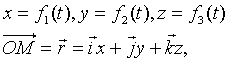 – параметрические уравнения траектории.
где – параметрические уравнения траектории.
где  - единичные векторы (орты), - единичные векторы (орты),
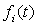 - непрерывны и 2 раза дифференцируемы; 2-е производные – непрерывны.
Непрерывная последовательность точек среды (пространства), занимаемая точкой M, называется траекторией точки М.
Исключая время: - непрерывны и 2 раза дифференцируемы; 2-е производные – непрерывны.
Непрерывная последовательность точек среды (пространства), занимаемая точкой M, называется траекторией точки М.
Исключая время:
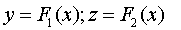 или:
или:
 Введём понятия скорости и ускорения:
Введём понятия скорости и ускорения:
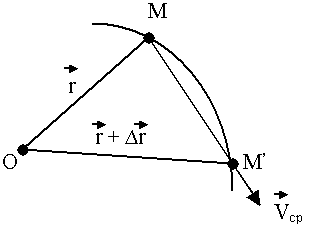
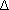 Рис.32.
т. М Рис.32.
т. М  t
т. М’ t
т. М’ t + t + 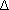 t
( t
(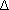 t - конечное).
Радиусы – векторы: t t - конечное).
Радиусы – векторы: t  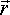 t +
t + 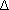 t t  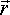 + + 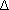 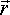
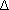 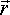 = = 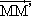 За время
За время 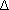 t (рис. 32): t (рис. 32):
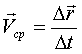 (Направление по секущей MM’).
Скорость точки в момент времени t получается при (Направление по секущей MM’).
Скорость точки в момент времени t получается при 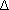 t t  0, то есть 0, то есть
 (Направление по касательной и траектории точки)
Очевидно: (Направление по касательной и траектории точки)
Очевидно:
 Проекции
Проекции  : :
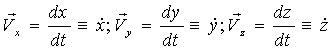 .
Модуль (длина): .
Модуль (длина):
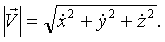 Скорость точки М в момент времени t равна производной по времени от радиуса – вектора точки и направлена по касательной к траектории.
Аналогично найдём ускорение (рис. 33).
Скорость точки М в момент времени t равна производной по времени от радиуса – вектора точки и направлена по касательной к траектории.
Аналогично найдём ускорение (рис. 33).
 Рис.33.
Совмещая начало векторов
Рис.33.
Совмещая начало векторов  (t) и (t) и  (t + (t + 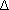 t) в точке М => t) в точке М => 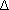  за за 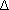 t.
Среднее ускорение: t.
Среднее ускорение:
 (направление в сторону вогнутости траектории)
Ускорение точки в момент времени t получается при (направление в сторону вогнутости траектории)
Ускорение точки в момент времени t получается при 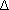 t t  0, то есть 0, то есть
 Очевидно:
Очевидно:

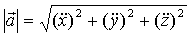 Ускорение точки в некоторый момент времени равно производной по времени от вектора скорости, или второй производной по времени от радиуса – вектора точки в этот момент времени.
В некоторых задачах – используется производная более высоких порядков, но здесь они пока не нужны.
В механике применяются не только декартовы координаты – часто применяют обобщённые (криволинейные) координаты.
Они бывают удобней, позволяют определить конфигурацию рассматриваемой системы. Часто их называют позиционными. Криволинейными они называются потому, что линии вдоль которых меняется только одна координата, обычно бывают кривыми.
Рассмотрим частный случай криволинейных координат – полярные координаты точки на плоскости: применим далее к задаче движение точек в центральном силовом поле (рис. 34).
Ускорение точки в некоторый момент времени равно производной по времени от вектора скорости, или второй производной по времени от радиуса – вектора точки в этот момент времени.
В некоторых задачах – используется производная более высоких порядков, но здесь они пока не нужны.
В механике применяются не только декартовы координаты – часто применяют обобщённые (криволинейные) координаты.
Они бывают удобней, позволяют определить конфигурацию рассматриваемой системы. Часто их называют позиционными. Криволинейными они называются потому, что линии вдоль которых меняется только одна координата, обычно бывают кривыми.
Рассмотрим частный случай криволинейных координат – полярные координаты точки на плоскости: применим далее к задаче движение точек в центральном силовом поле (рис. 34).
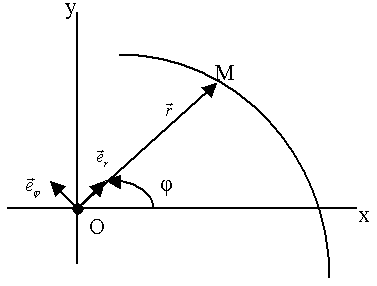 Рис.34.
(x, y) – декартовы координаты.
(r,
Рис.34.
(x, y) – декартовы координаты.
(r,  ) – полярные координаты.
Угол ) – полярные координаты.
Угол  => от Ох против часовой стрелки – положительное направление
Формулы преобразования:
x = r cos => от Ох против часовой стрелки – положительное направление
Формулы преобразования:
x = r cos , y = r sin , y = r sin , где r , где r 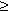 0; 0 0; 0   < 2 < 2 (можно рассматривать и
(можно рассматривать и   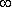 ).
Если r = const – концентрические окружности с центром в точке О.
Если ).
Если r = const – концентрические окружности с центром в точке О.
Если  = const – прямолинейные лучи из точки О.
Введём два орта: = const – прямолинейные лучи из точки О.
Введём два орта:
 Найдём производные
Найдём производные  по углу по углу  (рис. 35): (рис. 35):
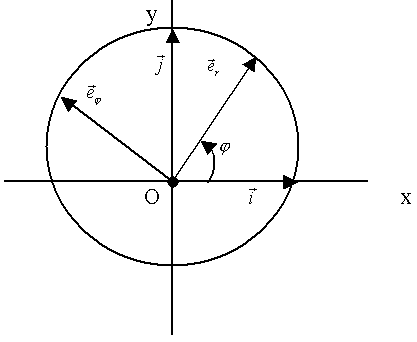 Рис.35.
Рис.35.
 (так как r = 1) (так как r = 1)
 при при  ,
т. е. ,
т. е. 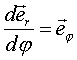 .
Далее: .
Далее:
 при при  ,
т. е. ,
т. е. 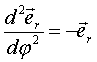 .
При каждом дифференцировании по φ т. е. происходит поворот на угол .
При каждом дифференцировании по φ т. е. происходит поворот на угол  .
Выведем формулы проекции скорости и ускорения точки М на направления касательных к координатным линиям в полярных координатах.
Так как .
Выведем формулы проекции скорости и ускорения точки М на направления касательных к координатным линиям в полярных координатах.
Так как 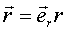 , то , то
 Но:
Но:  Очевидно:
Очевидно:
 Для ускорения:
Для ускорения:
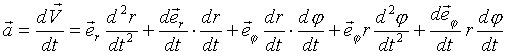 .
Но: .
Но:  .
Очевидно: .
Очевидно:
 Контрольные вопросы:
1. Что изучает кинематика?
2. Дайте определение скорости точки.
3. Напишите формулы проекций ускорения на оси полярной системы координат.
Контрольные вопросы:
1. Что изучает кинематика?
2. Дайте определение скорости точки.
3. Напишите формулы проекций ускорения на оси полярной системы координат.
|
| 9. Естественные координаты |
Рассмотрим систему координатных осей, определяемую траекторией точки (рис.36).
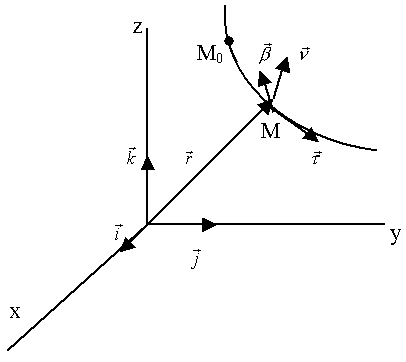 Рис.36.
Рис.36.
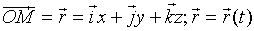 .
Единичный вектор касательной к траектории (S – длина дуги М0М): .
Единичный вектор касательной к траектории (S – длина дуги М0М):
 , где , где  .
Дифференцируя .
Дифференцируя  по S: по S: 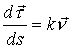 ,
где ,
где 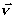 - единичный вектор главной нормали; - единичный вектор главной нормали; 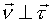 и направлен в сторону вогнутости; и направлен в сторону вогнутости;
 кривизна. (k = 0 - прямая); кривизна. (k = 0 - прямая); 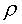 - радиус кривизны.
Единичный вектор бинормали - радиус кривизны.
Единичный вектор бинормали 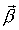 : :
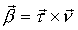 . .
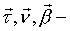 образуют правую тройку ортогональных единичных векторов. Они определяют направление естественных (натуральных) осей в том месте траектории, где находится движущаяся точка. образуют правую тройку ортогональных единичных векторов. Они определяют направление естественных (натуральных) осей в том месте траектории, где находится движущаяся точка.
 соприкасающаяся соприкасающаяся 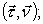
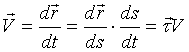 Очевидно, проекция на ось
Очевидно, проекция на ось  : :  (может иметь разные знаки – зависит от направления S).
Для ускорения: (может иметь разные знаки – зависит от направления S).
Для ускорения:
 ;
Но: ;
Но:  ;
Очевидно, проекции ускорения на естественные оси:
на касательную: ;
Очевидно, проекции ускорения на естественные оси:
на касательную: 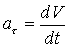 ;
на главную нормаль: ;
на главную нормаль:  на бинормаль: 0
Таким образом, ускорение лежит в соприкасающейся плоскости (рис. 37).
на бинормаль: 0
Таким образом, ускорение лежит в соприкасающейся плоскости (рис. 37).
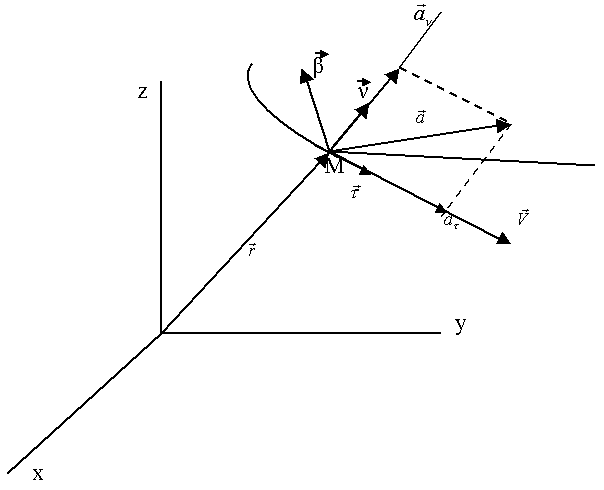 Рис.37.
Задача.
Рис.37.
Задача.
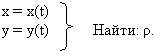
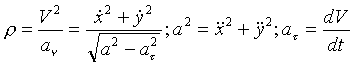 Контрольные вопросы:
1. Какие основные отличия естественной системы координат от декартовой?
2. Назовите проекции скорости точки в естественных координатах.
3. Какова последовательность определения радиуса кривизны траектории точки?
Контрольные вопросы:
1. Какие основные отличия естественной системы координат от декартовой?
2. Назовите проекции скорости точки в естественных координатах.
3. Какова последовательность определения радиуса кривизны траектории точки?
|
| 10. Формула Эйлера |
Найдём число координат, определяющих положение абсолютно твёрдого тела.
Определить положение тела => определить координаты  точки относительно некоторой системы отсчёта в точки относительно некоторой системы отсчёта в  момент времени. момент времени.
 Рис.38.
Пусть Х1 , Х2, Х3 – неподвижные оси (рис. 38); орты:
Рис.38.
Пусть Х1 , Х2, Х3 – неподвижные оси (рис. 38); орты:  [декартова система]. [декартова система].
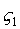 , ,  , , 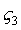 - оси, жёстко связанные с телом; орты: - оси, жёстко связанные с телом; орты:  , ,  , , 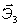 - [декартова система].
Так как координаты точек относительно собственных осей - [декартова система].
Так как координаты точек относительно собственных осей 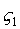 , , , ,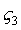 не зависят от времени, то задача сводится к определению положения координатных осей, жёстко связанных с телом (подвижных), относительно неподвижных осей Х1 , Х2, Х3.
Составим таблицу косинусов углов между осями Х и не зависят от времени, то задача сводится к определению положения координатных осей, жёстко связанных с телом (подвижных), относительно неподвижных осей Х1 , Х2, Х3.
Составим таблицу косинусов углов между осями Х и  : :
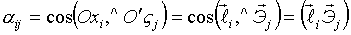
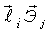 - скалярное произведение. - скалярное произведение.
 Так как системы координат ортогональны, то
скалярное произведение:
Так как системы координат ортогональны, то
скалярное произведение:  , где , где 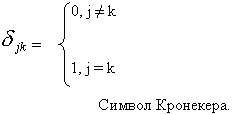
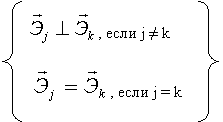

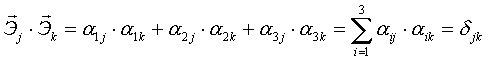 Итак:
Итак: Число таких соотношений = 6 (Из 9 – ти в силу симметрии по jи k).
Число таких соотношений = 6 (Из 9 – ти в силу симметрии по jи k).
 Имеем 6 соотношений для 9 косинусов =>
3 косинуса Имеем 6 соотношений для 9 косинусов =>
3 косинуса 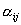 , не расположенные в одном столбце, или в одной строке, могут быть приняты за независимые, а остальные можем определить из составленных 6 – ти соотношений.
Кроме того => три координаты определяют положение точки О’ – начало системы , не расположенные в одном столбце, или в одной строке, могут быть приняты за независимые, а остальные можем определить из составленных 6 – ти соотношений.
Кроме того => три координаты определяют положение точки О’ – начало системы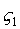 , ,  , , 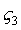 .
Но 9 координат и 3 соотношение длин: .
Но 9 координат и 3 соотношение длин:
 Это условия постоянства расстояний между точками в абсолютно твёрдом теле.
Выведем формулу Эйлера для распределения скоростей точек абсолютно твёрдого тела (рис. 39).
Это условия постоянства расстояний между точками в абсолютно твёрдом теле.
Выведем формулу Эйлера для распределения скоростей точек абсолютно твёрдого тела (рис. 39).

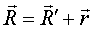 ,
1) ,
1)  , ,
 - скорость точки О’, - скорость точки О’,
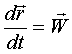 - скорость точки Q во вращательном движении тела (так как длина - скорость точки Q во вращательном движении тела (так как длина  постоянна).
Так как координаты постоянна).
Так как координаты 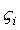 точки Qпостоянны, то точки Qпостоянны, то
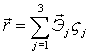 Тогда:
2)
Тогда:
2)  ,
где ,
где 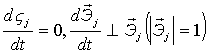 .
Скорость точки Q: .
Скорость точки Q:  .
3) Выразим .
3) Выразим 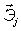 и производные через направляющие косинусы и производные через направляющие косинусы  : :
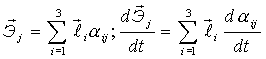 .
Тогда: .
Тогда: 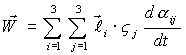 (в неподвижной системе).
4) Проекция (в неподвижной системе).
4) Проекция 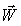 на ось на ось  (k= 1,2,3): (k= 1,2,3):
 .
Скорости точек во вращательном движении – линейные функции координат точек.
5) Получим более простую и наглядную форму закона распределения скоростей, используя свойства функции .
Скорости точек во вращательном движении – линейные функции координат точек.
5) Получим более простую и наглядную форму закона распределения скоростей, используя свойства функции 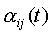 . .
 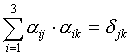 ,
Дифференцируем по t: ,
Дифференцируем по t:
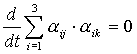 .
По свойству производной от произведения:
при j= k => .
По свойству производной от произведения:
при j= k =>  ,
при j≠ k=> ,
при j≠ k=> 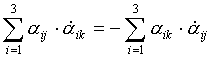 .
Свойства:
а) симметрия по kи j;
б) при j= k=>равенство «0»;
в) размерность t-1, т. е. угловая скорость (угол в радианах), так как .
Свойства:
а) симметрия по kи j;
б) при j= k=>равенство «0»;
в) размерность t-1, т. е. угловая скорость (угол в радианах), так как  - скорость.
г) различных только три => - скорость.
г) различных только три =>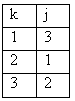 Покажем, что
Покажем, что
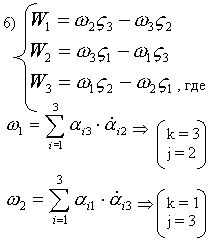
 Действительно:
Действительно:
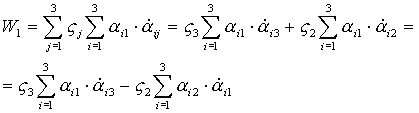
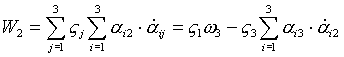
 - по аналогии.
Итак: - по аналогии.
Итак:
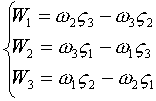 или:
7)
или:
7) 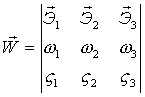 , где , где  - единичные вектора, жёстко связанные с телом.
Положим - единичные вектора, жёстко связанные с телом.
Положим  - вектор, где - вектор, где 
 
 8) Тогда:
8) Тогда:
Назовём Таким образом, закон распределения скоростей точек абсолютно твёрдого тела в любом движении:
Это формула Эйлера в векторной записи.
Контрольные вопросы: 1. Сколько координат определяют положение твёрдого тела в пространстве? 2. Что называется вектором мгновенной угловой скорости? 3. Напишите формулу Эйлера. | |||
| 11. Распределение ускорений точек твёрдого тела |
Найдём закон распределения.
Дифференцируем по времени формулу Эйлера:
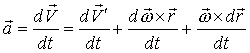 ,
Так как ,
Так как  , то , то
 => =>
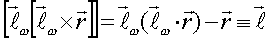 двойное векторное произведение
двойное векторное произведение 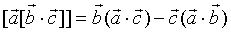
 - формула Ривальса для распределения
ускорений точек абсолютно твёрдого тела (рис. 40).
1) - формула Ривальса для распределения
ускорений точек абсолютно твёрдого тела (рис. 40).
1)  - ускорение начала подвижной системы.
Так - ускорение начала подвижной системы.
Так
Дата добавления: 2014-01-06; Просмотров: 477; Нарушение авторских прав?; Мы поможем в написании вашей работы! |
Генерация страницы за: 0.012 сек.
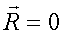
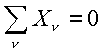

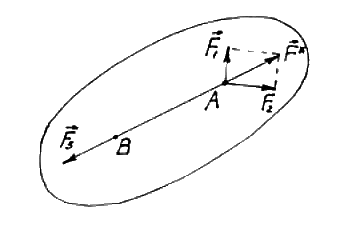
 равна по величине и противоположно направлена сумме
равна по величине и противоположно направлена сумме 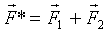 (рис.6).
(рис.6).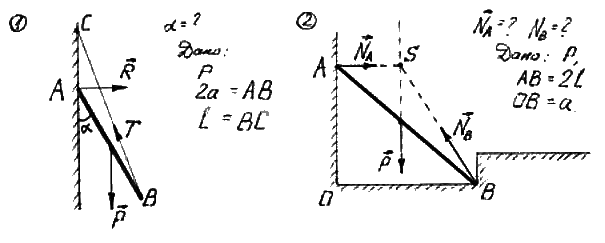

 относительно точки О определим как вектор
относительно точки О определим как вектор  или
или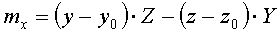


 ,
,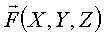 ;
;  ;
;  .
. , где F – модуль силы, h – плечо (расстояние от точки до направления силы).
, где F – модуль силы, h – плечо (расстояние от точки до направления силы).
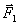 ||
|| 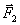 в плоскости
в плоскости 


 ,
,

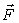 - результирующая сила через начало координат;
- результирующая сила через начало координат;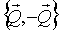 - результирующая пара, причём,
- результирующая пара, причём,  через точку О.
через точку О.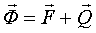
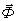 и
и 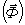 проходит через заданную точку О.
проходит через заданную точку О. на одной прямой, равны, направлены противоположно (аксиома 2).
на одной прямой, равны, направлены противоположно (аксиома 2).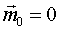 .
.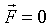 , так как остаётся только эта сила.
, так как остаётся только эта сила. .
.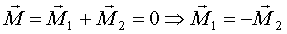 (рис.22)
(рис.22)
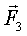 , ч.т.д. (Проще:
, ч.т.д. (Проще: 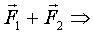 в плоскости
в плоскости  только там же для уравновешивания).
только там же для уравновешивания).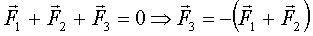
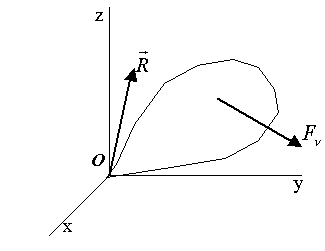

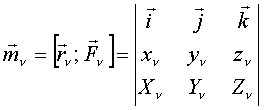
 ;
;  ;
; 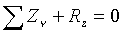 .
.
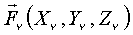 ; Rx, Ry, Rz в точке О; R`x, R`y, R`z в точке О1; ОО1 = h.
; Rx, Ry, Rz в точке О; R`x, R`y, R`z в точке О1; ОО1 = h.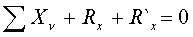
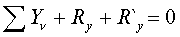

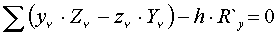


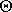 , который определяется из последнего уравнения:
, который определяется из последнего уравнения: 

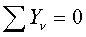
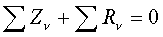
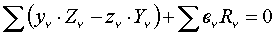
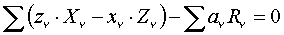
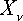 ,
,  ,
, 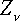 – проекции активных сил, приложенных в точках (
– проекции активных сил, приложенных в точках ( ,
, 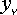 ,
,  ).
).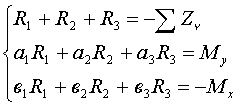 ,
,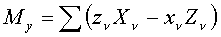 ,
,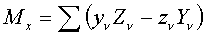 .
.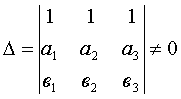 ,
,
 .
.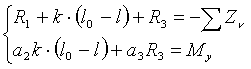
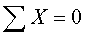
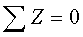
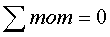
 А = 0
А = 0 



 вектором мгновенной угловой скорости, а прямая на которой он располагается, в рассматриваемый момент времени, проходящую через точку О ’ – осью мгновенного вращения, или мгновенной осью.
вектором мгновенной угловой скорости, а прямая на которой он располагается, в рассматриваемый момент времени, проходящую через точку О ’ – осью мгновенного вращения, или мгновенной осью.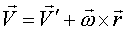 .
.