Метод фазових траєкторій

Метод фазових траєкторій (фазового простору, фазової площини) – графоаналітичний метод наближеного дослідження нелінійних систем. Суть метода полягає в оцінці поведінки системи за допомогою наочних геометричних уявлень – фазових параметрів. Фазовий простір (простір станів) – простір в прямокутній системі координат, якими є вихідна змінна та (n-1) її похідних. Кількість фазових координат дорівнює порядку системи n, тому для системи другого порядку (n=2) фазовий простір є 2-х вимірним, тобто перетворюється у фазову площину. В цьому випадку термін “фаза” має таке ж значення, що і “стадія”, тобто розвиток, зміна стану. Точка з координатами (x_i, x_j) називається зображуючою, а лінія, по якій вона переміщується при зміні стану системи – фазовим портретом. Це сукупність траєкторій, які визначають множину груп початкових умов та розв’язок диференціальних рівнянь системи. Фазові траєкторії дають повне уявлення про характер процесів в системі, крім часових оцінок, тому що час з розгляду процесів виключається.

Якщо розглядати в системі стабілізації відхилення то усталеному стану буде відповідати точка 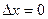, тобто початок координат. Цей стан відповідає так званій особливій точці. Різним фазовим траєкторіям відповідають різні особливі точки. Наприклад, для лінійних стійких систем всі фазові траєкторії асимптотично стягуються в початок координат, а у випадку нестійких систем – прямують в нескінченінсть.

З розгляду наведеного матеріалу можна зробити висновок, що найбільш зручним є метод фазової площини. Запишемо диференціальне рівняння системи другого порядку:

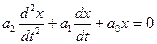(1.1)

Будемо вважати, що х – вихідна координата системи і приймемо х₁=х, тоді:

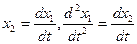(1.2)

Рівняння (1.1) запишемо у вигляді двох рівнянь 1-го порядку:

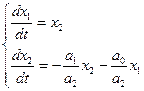або (1.3)

Розділимо друге рівняння в (1.3) на перше:

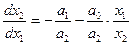(1.4)

Після інтергування отримуємо рівняння фазових траєкторій:

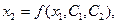(1.5)

де: С₁, С₂ – постійні інтегрування. Вид функції залежить від коефіцієнтів а_i, які визначають корені характеристичного поліному системи:

(1.6)

корені рівняння:

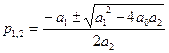(1.7)

В методі фазової площини головним, визначальним моментом є те, що кожному перехідному процесу в системі відповідає своя фазова траєкторія. Вид коренів рівняння (1.6) розглядався в розділі, присвяченому стійкості автоматичних систем (частина перша). На рис. 1.4 показана відповідність перехідних процесів і фазових траєкторій НЛС, що відповідає комплексним попарно спряженим кореням з від’ємною (а) та додатною (б) дійсними частинами і уявними (в). Можна знайти також інші перехідні процеси, наприклад, аперіодичні та відповідні фазові портрети.

а)

б)

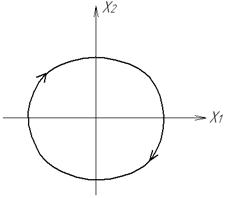
в)

Рис.1.4. Перехідні процеси і фазові траєкторії НЛС

а) стійкої; б) нестійкої; в) на межі стійкості

Аналіз перехідних процесів та відповідних фазових портретів НЛС приводить до таких результатів:

- стійкому коливальному процесу відповідає фазова траєкторія, яка збігається до початку координат (рис.1.4,а). Особливою точкою тут є стійкий фокус;

- нестійкому коливальному процесу відповідає фазова траєкторія, яка віддаляється від початку координат, особливо точка – нестійкий фокус (рис.1.4,б);

- періодичному процесу (автоколиванням) відповідає замкнена фазова траєкторія (коло або еліпс), яка називається граничним циклом (рис.1.4,в), особлива точка – центр.

Для інших фазових траєкторій особливими точками можуть бути стійкий або нестійкий вузол, сідло.

За графіком граничного циклу можна наближено визначити параметри автоколивань: частота 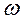характеризується відношенням відрізків на осях х₂ до х₁, а амплітуда дорівнює відрізку на х₁.

Фазові траєкторії НЛС мають свої особливості. Це викликано тим, що для лінійної системи характер особливої точки повністю визначає її поведінку при будь-яких відхиленнях від стану рівноваги, тобто стійкість лінійної системи не залежить від величини збурення і ця властивість зберігається у всіх точках фазового простору. Для НЛС характер особливої точки визначає поведінку фазових траєкторій лише поблизу точки рівноваги. Може бути такий випадок: стан рівноваги НЛС нестійкий, перехідний процес розбіжний, але він може перейти в стійкий граничний цикл (рис.1.5).

а) б) в)

Рис.1.5. Фазові траєкторії нелінійних систем

а) стійкий граничний цикл; б) нестійкий граничний цикл; в) два граничних цикли

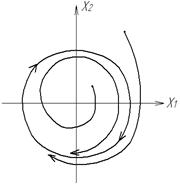
Якщо в нелінійній системі є суттєві зони нечутливості та сухого тертя, то усталеному стану відповідає не один режим, а область, і особлива точка “витягується” в особливу лінію(рис.1.6).

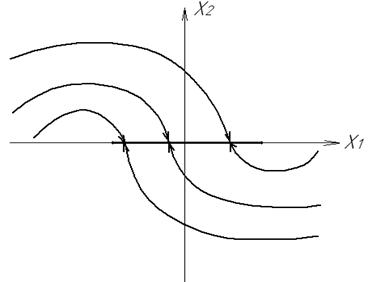
Рис.1.6. Фазові траєкторії НЛС із зоною нечутливості і сухим тертям

В залежності від особливостей НЛС в них можуть бути автоколивання:

- з м’яким режимом збудження, коли після включення завжди система переходить в режим автоколивань не залежно від початкових умов і зовнішніх збурень;

- з жорстким режимом збудження, коли для виникнення автоколивань, які відповідають стійкому циклу, необхідно створити достатньо велике початкове відхилення. Наприклад, зображуюча точка знаходиться поза стійким граничним циклом, а під впливом зовнішніх сигналів вона може перейти на цей цикл або переміститись всередину цикла, і автоколивання затухнуть.

Фазовий портрет НЛС може мати кусково-лінійні або розривні характеристики, складатись з кількох областей з різними фазовими траєкторіями. В цьому випадку на фазовому портреті є лінії перемикання, які відділяють одну область від іншої.

Розроблено метод наближеної побудови фазових портретів НЛС, який дістав назву методу припасовування (зшивання), коли характеристики нелінійностей подаються у вигляді кусково-лінійних залежностей (ламаною лінією). Це відповідає тому, що в правій частині рівняння фазових траєкторій буде набір кількох лінійних функцій для лінійних дільниць характеристики нелінійної ланки. В процесі зміни х₁ та х₂ відбувається заміна однією функції на іншу в момент проходження через точки зламу. В результаті фазова характеристика розбивається на ряд дільниць, в межах кожної з яких їх рівняння є лінійними і легко інтегруються. Таким чином, точки зламу кусково-лінійної характеристики відповідають лінії переключення, зміни правої частини рівняння (рис.1.7), де показана лінія перемикання АВСD для системи другого порядку.

Рис.1.7. Лінія перемикання для системи 2-го порядку

Рис.1.8. Фазовий портрет системи з релейним елементом

Для НЛС з релейним 2-х позиційним елементом фазовий портрет показаний на рис.1.8. Лінія перемикання співпадає з віссю х₂ (х₁=0). Для НЛС з релейними елементами існує ковзний режим, коли зображаюча точка переміщується по лінії переключення, наближаючись до початку координат (“ковзає”). Перехідний процес в релейній системі протікає як в неперервній системі. При цьому релейний елемент переключається з достатньо великою частотою, а ковзний режим (коливання навколо лінії переключення) створює ефект вібраційної лінеаризації.

Крім метода припасовування (зшивання) для побудови фазових портретів НЛС використовується метод ізоклін – кривих з однаковим нахилом фазових траєкторій, які проходять через точки цих кривих.

Головним методом дослідження НЛС є використання ЕОМ: визначається кількість і характер можливих станів рівноваги, кількість граничних циклів і їх взаємне розташування, що дає можливість оцінити сукупність можливих режимів роботи системи. Виконуються також розрахунки для найбільш важливих початкових умов.

1.4. Проходження випадкового сигналу через нелінійну ланку. Статистична лінеаризація

При діянні на НЛС стаціонарного випадкового сигналу виникає відповідний режим роботи, який характеризується, в першу чергу, оцінками математичного сподівання та дисперсії.

Для прикладу розглядається нелінійна ланка, яка має статичну характеристику з насиченням (рис.1.9,а,б). На вхід НЛ поступає стаціонарний випадковий сигнал

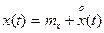(1.8)

з нормальним розподіленням, графік якого показано на рис.1.9,в. Вихідний сигнал

(1.9)

має щільність ймовірності розподілення, показаний на рис.1.9,г.

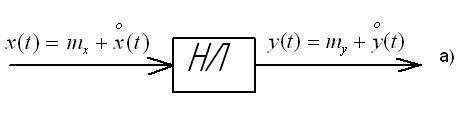
Рис.1.9. Змінювання розподілення сигналу

Значення х, які лежать всередині лінійної частини характеристики ланки, проходять без змін (коефіцієнт передачі ланки прийнято рівним одиниці). Всі значення 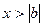дають на виході постійне значення y, тобто ймовірність появи сигналу дорівнює нулю. Це відображається нескінченно вузькими імпульсами на межах діапазону , площі яких відповідають заштрихованим площам на графіку рис.1.9,в. Ці імпульси умовно показані кінцевої ширини і висоти.

Якщо змінюється m_x, то змінюються також і m_y та D_y, зокрема при збільшенні m_x величина m_y також зростає, наближаючись до b, а D_y буде зменшуватись до нуля, коли m_x >>b. Якщо при m_x=const звужувати або розширяти криву р(х), змінюючи D_х, то будуть змінюватись як m_y, так і D_y. При звуженні кривої р(х) величина m_y буде збільшуватись, прямуючи до m_x, коли крива р(х) буде входити в діапазон , а дисперсія D_х і D_y .

Таким чином, при проходженні випадкового сигналу через нелінійну ланку закон розподілення щільності ймовірності змінюється, а m_y та D_y кожна залежать від m_х та D_х, тобто принцип суперпозиції не виконується.

Крім того, наявність випадкової складової сигналу приводить до згладжування нелінійної залежності між виходом і входом для середнього значення (детермінованої складової). Таким чином, випадкова складова вхідного сигналу створює ефект лінеаризації нелінійної ланки для детермінованої складової сигналу. В цьому випадку навіть релейна система поводить себе як ланка неперервної дії. При збільшенні m_х передача ланкою випадкової складової ослаблюється за рахунок того, що ланка насичується детермінованою складовою сигналу.

На викладених закономірностях базується наближений метод статистичної лінеаризації НЛС, який полягає в заміні нелінійної системи еквівалентною лінійною щодо реакції на заданий вхідний сигнал. Таким чином, необхідно підібрати таку лінійну еквівалентну ланку, яка з достатньою точністю відтворює вихідний сигнал нелінійної ланки.

Приймається, що на вході та виході нелінійної ланки діють відповідно сигнали, які описуються залежностями (1.8), (1.9). Тоді для лінійної еквівалентної ланки можна записати:

(1.10)

де: k₀, k₁ – коефіцієнти статистичної лінеаризації (рис.1.10).

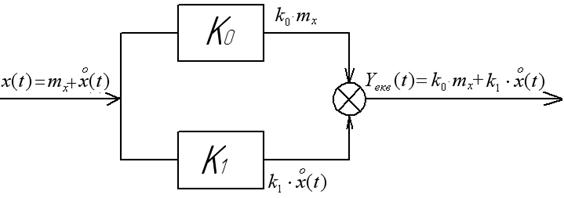
Рис.1.10. Структура еквівалентної лінійної ланки

Для заміни нелінійної ланки еквівалентною лінійною необхідно знайти вирази для коефіцієнтів k₀ і k₁. Часто ці коефіцієнти знаходять, використовуючи такі критерії:

- забезпечення незмінних значень:

(1.11)

- мінімум середньоквадратичного відхилення:

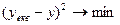(1.12)

За обома критеріями коефіцієнт

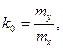(1.13)

а другий коефіцієнт

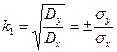- за першим критерієм (1.14)

- за другим критерієм (1.15)

Формули (1.14), (1.15) строго виводяться, а знак у виразі (1.14) приймається так: k₁>0, коли в точці х= m_x функція f(x) зростає, і k₁<0 – в протилежному випадку. Можна приймати середнє значення k₁, визначене за формулами (1.14), (1.15). Наближеність такого методу лінеаризації пов’язана з припущенням щодо нормального закону розподілення вхідного сигналу та нехтуванням його змінювання нелінійною ланкою. Еквівалентна лінійна ланка точно відтворює змінювання m_x і наближено -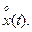

Дата добавления: 2014-01-06