Спеціальні системи

В теорії автоматичного керування виділяють клас спеціальних систем, до яких відносяться:

- системи із запізнюванням;

- нестаціонарні системи;

- системи з розподіленим параметрами;

В системах із запізнюванням вихідний сигнал відстає від вхідного на час 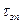. Коли відношення 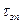до постійного часу Т складає, таке запізнювання є суттєвим в системі, а в реальних системах це відношення може складати 2÷5. Запізнювання в системах керування є, за рідким винятком шкідливим, і при використанні типових регуляторів приводить до погіршення якості перехідних процесів або навіть до втрати стійкості.

Диференціальні рівняння систем із запізнюванням в явному вигляді включають аргумент 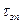, наприклад для аперіодичної ланки:

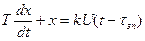(2.41)

Часова характеристика, яка відповідає рівнянню (2.39), показана на рис.2.8.

Рівняння (2.39) записати у вигляді:

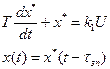(2.42)

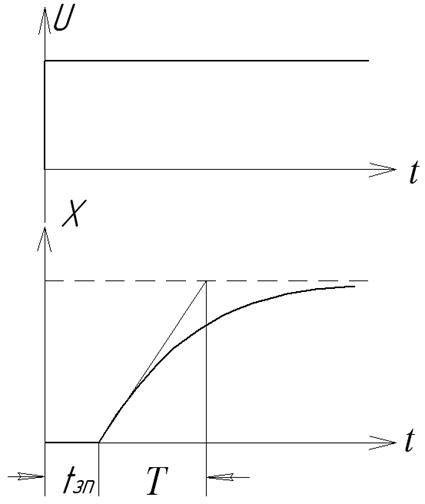
Рис.2.8. Часова характеристика ланки із запізнюванням

В цьому випадку запізнювання є транспортним (чистим). При послідовному з’єднанні кількох аперіодичних ланок проявляється так зване ємкісне запізнювання.

Передаточна функція системи із запізнюванням подається у вигляді:

(2.43)

де: 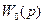- передаточна функція всіх елементів без запізнювання.

Частотна характеристика такої системи:

(2.44)

Наявність запізнювання не змінює амплітуду, але повертає кожен вектор за годинниковою стрілкою на кут 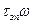, при цьому 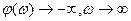. Отже, годограф має спіральну форму і асимптотично наближається до початку координат. При цьому, як правило, погіршується стійкість та існує критичне значення часу запізнювання 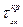, при якому система виходить на межу стійкості.

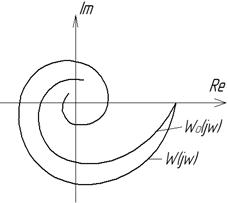
Рис.2.9. Частотні характеристики систем із запізнюванням

Елемент запізнювання може знаходитись в різних частинах системи, наприклад в прямому контурі (рис.2.10)

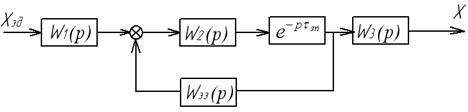
Рис.2.10. Структура системи з елементом запізнювання в прямому контурі

Передаточна функція замкненої системи буде:

(2.45)

Елемент запізнювання може знаходитись і в місцевому зворотньому зв’язку (послідовно з передаточною функцією 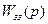). Тоді передаточна функція замкненої системи буде:

(2.46)

Як видно з виразів (2.45), (2.46) характеристичне рівняння системи із запізнюванням є трансцендентним, включає показникову функцію, і для оцінки стійкості системи не можна використовувати алгебраїчні критерії. В той же час зручнішими є частотні критерії, має значення форма годографа частотної характеристики.

Умовою знаходження системи на межі стійкості за критерієм Найквіста є:

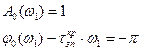(2.47)

Звідки значення критичного запізнення буде:

(2.48)

Приклад. Розглянемо систему, яка складається з послідовно з’єднаних аперіодичної ланки і ланки запізнювання:

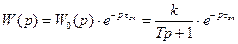(2.49)

Тоді:

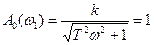(2.50)

звідки:

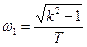(2.51)

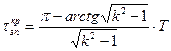(2.52)

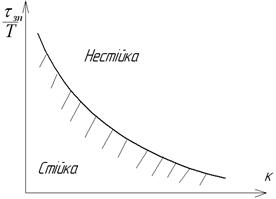
Рис.2.11. Область стійкості системи із запізнюванням

На рис.2.11 показана область стійкості системи із запізнюванням на площині її параметрів . Якщо запізнювання відсутнє, система стійка при будь-якому 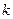. В будь-якому випадку наявність запізнювання звужує область стійкості системи.

Для зменшення шкідливого впливу запізнювання застосовуються багатоконтурні системи, в яких формується сигнал за похідною регульованої координати, але більш ефективним способом є використання спеціальних пристроїв для прогнозування запізнювання, наприклад статистично оптимальний алгоритм прогнозування. Ефективними є також спеціальні регулятори (прогнозатори), відомі в технічній літературі як регулятори Сміта і Ресвіка.

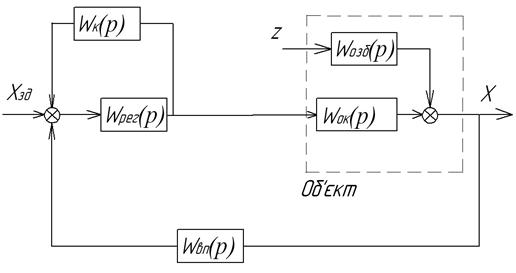
Рис.2.12. Регулятор (прогнозатор) Сміта

Регулятор (прогнозатор) Сміта (рис.2.12) включає компенсатор з передаточною функцією:

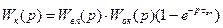(2.53)

де: 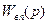- передаточна функція вимірювального пристрою (в частинному випадку ).

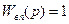При відсутності компенсатора вихід замкненої системи буде:

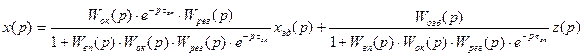(2.54)

Характеристичне рівняння включає 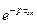і є трансцендентним. Після введення компенсатора вихід системи буде:

(2.55)

а характеристичне рівняння не включає запізнювання. В цьому випадку можна обирати достатньо великі коефіцієнти передачі системи, що покращує якість перехідних процесів (рис.2.13):

1 – без компенсатора;

2 – з компенсатором;

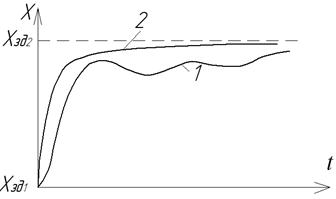
Рис.2.13. Перехідні процеси в системі із запізнюванням.

Нестаціонарними системами керування називаються такі, параметри яких в процесі функціонування змінюються. Прикладом можуть бути різні об’єкти з різних галузей: в технологічних агрегатах змінюються коефіцієнти тепло- і масообміну; в літаках – запас (маса) палива; в роботах маса вантажів і т.д.

Динаміка нестаціонарних систем описується диференціальними рівняннями із змінними коефіцієнтами:

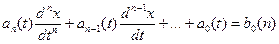(2.56)

Закономірності змінювання коефіцієнтів 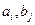можуть бути відомими, наприклад як функції часу, або змінюватись довільно. В будь-якому випадку особливістю нестаціонарних систем є залежність динамічних властивостей і характеристик від поточного моменту часу, тобто в задачах аналізу та синтезу систем керування щоразу фігурує „новий об’єкт”. Крім того, рівняння із змінними коефіцієнтами потребують використання для отримання їх розв’язків спеціальних методів.

В практичних задачах нестаціонарну систему замінюють квазістаціонарною, для чого використовують методи:

- „заморожених” коефіцієнтів. На всьому інтервалі роботи системи обирається ряд послідовних моментів часу, коли коефіцієнти рівняння (2.54), тобто параметри системи приймають граничні або критичні по відношенню до динаміки значення. Для кожного інтервалу часу розраховуються параметри регуляторів та елементів корекції;

- „заморожених” реакцій. Це більш точний, але більш складний метод. В системі виділяється одна ланка, яка має змінювані параметри, а решта ланок приймається з постійними параметрами. Для ланки із змінюваними параметрами визначається еквівалентна передаточна функція з постійними коефіцієнтами, яка і приймається при розрахунках.

Значною проблемою при створенні і дослідженні нестаціонарних систем є оцінки їх стійкості і якості. Для таких систем не можна використовувати поняття асимптотичної стійкості 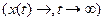. В цьому випадку розгядається лише так звана „технічна стійкість” на кінцевому інтервалі часу 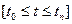, коли регульована координата не виходить за межі визначених наперед значень. Такі ж вимоги ставляться щодо показників якості.

При розгяді властивостей об’єктів керування відзначалось, що для багатьох з них характерна розподіленість параметрів. В системах з розподіленими параметрами в кожній точці об’єкта виникають свої перехідні процеси, які залежать від часу і від просторової координати. В сукупності локальні перехідні процеси утворюють загальний процес розповсюдження сигнала, який в залежності від характера (аперіодичний або коливальний) називають потоком або хвилею. Перехідні процеси в таких системах описуються диференціальними рівняннями в частинних похідних.

В задачах аналізу та синтезу систем з розподіленими параметрами виділяють окремо ланки, коефіцієнти яких залежать від просторової координати, а решту розглядають в припущенні щодо зосередженості параметрів. Для таких систем необхідно враховувати ряд особливостей:

- порядок розподіленої системи - кількість змінних стану, тобто порядок диференціального рівняння відносно часу t;

- отримати рівняння в змінних стану для цих систем неможливо, тому виділяють мінімально необхідний набір змінних, який необхідний для опису системи, зокрема для можливості прогнозу майбутніх станів системи;

- розмірність розподіленої системи – число геометричних координат, необхідних для повного опису процесів в сукупності, для континіума точок.

Типовими об’єктами з розподіленими параметрами є трубчасті теплообмінники, в яких відношення довжини труби до діаметра складає 10 і більше; електричні лінії; газо- та водопроводи; технологічні агрегати значного об’єму і інші.

Диференціальні рівняння, які описують динаміку об’єктів з розподіленими параметрами, подають у вигляді:

- для електричної лінії:

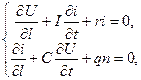(2.57)

де: 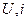- напруга та струм вздовж лінії;

- індуктивність, ємність, опір та провідність на одиницю довжини лінії;

- теплообмінника „труба в трубі”:

(2.58)

де: 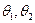- температури теплоносіїв; 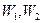- швидкість; 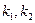- коефіцієнти, які залежать від поверхні теплообміну, коефіцієнтів тепловіддачі і інших параметрів об’єкта.

При дослідженні систем з розподіленими параметрами визначаються граничні умови на обох кінцях об’єкта, з урахуванням яких розв’язуються рівняння в частинних похідних. Отримують трансцендентну передаточну функцію, яка включається в систему звичайних передаточних функцій і інших ланок. Окремою задачею є створення систем розподіленого контролю.

[1, с.31-49, 2, с.228-246, 367-400]

Дата добавления: 2014-01-06