Вопросы. Формулы полной вероятности, Бейеса, Бернулли

Формулы полной вероятности, Бейеса, Бернулли. Теоремы Лапласа.

Основные понятия. Теоремы сложения и умножения.

Лекция 13

Элементы теории вероятностей

1. Предмет теории вероятности.
2. Виды событий.
3. Классическое определение вероятности.
4. Статистическое определение вероятности.
5. Геометрическое определение вероятности.
6. Теорема сложения вероятностей несовместных событий.
7. Теорема умножения вероятностей независимых событий.
8. Условная вероятность.
9. Умножение зависимых событий.
10. Сложение совместных событий.
11. Формула полной вероятности.
12. Формула Бейеса.

13. Биноминальный, полиномиальный закон распределения .

14. Локальная теорема Лапласа .

15. Интегральная теорема Лапласа, с таблицы .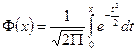

16. Свойства , теорема Пуассона.

17. Формула Пуассона .

1. Предмет теории вероятностей. Основные понятия

Большинство закономерностей, которые нами рассматривались, были детерминированными процессами. Например, в математике: через две точки можно провести прямую и притом только одну, в физике: если в нормальных условиях воду нагреть до 100 градусов, то она закипит. Но часто встречаются случайные события.

Событием в теории вероятностей называют всякий факт, который может произойти в результате некоторого опыта (испытания).

Например: Стрелок стреляет по мишени. Выстрел – испытание, попадание в мишень – событие. События принято обозначать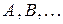

Единичное случайное событие – следствие очень многих случайных причин, которые очень часто невозможно учесть. Однако, если рассматривать массовые однородные события (многократно наблюдающиеся при осуществлении опыта в одних и тех же условиях), то они оказываются подчиняются определенным закономерностям: если бросать монету в одних и тех же условиях большое число раз, можно с небольшой погрешностью предсказать, что число появлений герба будет равно половине числа бросков.

Предметом теории вероятностей является изучение вероятностных закономерностей массовых однородных случайных событий. Методы теории вероятностей широко применяются в теориях надежности, стрельбы, автоматического управления и т.д. Теория вероятности служит обоснованием математической и прикладной статистики, которая в свою очередь используется при планировании и организации производства, при анализе технологических процессов и т.д.

Дата добавления: 2014-01-06