Эмпирическая функция распределения

Основная задача математической теории выборочного метода.

Определение 1. Все множество объектов, подлежащих контролю и исследованию, называется генеральной совокупностью.

Определение 2. Множество, случайным оборазом отобранных объектов, называется выборочной совокупностью.

Определение 3. Число объектов выборочной совокупности (или генеральной совокупности) называют объемом выборки (или генеральной совокупностью).

Например, если из 10000 деталей отобрано для контроля 100, то говорят N=10000 – генеральная совокупность, n=100 - объем выборки.

Обычно генеральная совокупность содержит конечное множество объектов. Но оно достаточно велико, поэтому при теоретических выводах объем генеральной совокупности часто предполагается бесконечным. Это оправдывается тем, что увеличение обема генеральной совокупности уже не сказывается на результатах отработки данных выборки.

Для объектов генеральной совокупности определяется некоторая числовая характеристика – это случайная величина 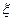, принимающая на каждом объекте некоторое числовое значение. Сделав выборку, мы получаем ряд значений этой случайной величины 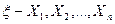. По этой последовательности значений нам следует приблизительно представить функцию распределения случайно величины 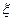, ее математическое ожидание и дисперсию.

В 1933г. советский математик В.И. Гливенко была доказан основная теорема математической статистики, из которой следует правило для приближенного получения функции распределения случайной величины 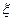. Смысл ее в следующем: для любого действительного числа х обозначим частот чисел 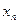из выборки 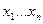, удовлетворяющих неравенству 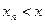. Этим на всей числовой прямой определена функция . Положим 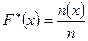. Эта функция называется функцией распределения выборки случайной величины 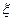. Она идает приближенную функцию распределения 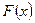случайно величины .

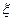Пример. В результате выборки имеем

-3,+2,-1,-3,+5,-3,+2. Потсроить график эмпирической функции распределения.

Решение. .

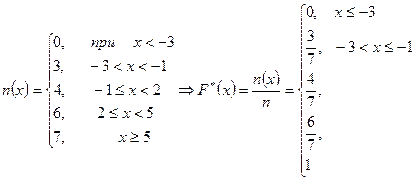
На примере видны основные особенности эмпирической функции распределения. Как и теоретическая, она не убывает, и ее значения 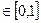. Но эта формула всегда ступенчатая. Эмпирическая функция не зависит от того, в каком порядке сделана выборка, т.е. от того, в каком порядке идут числа в последовательности: .

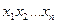Дата добавления: 2014-01-06