
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Частные приращения и частные производные
|
|
|
|
В отличие от функций одной переменной, функций нескольких переменных имеют различные виды приращений. Это связано с тем, что перемещения в плоскости  из точки
из точки  можно осуществлять по различным направлениям.
можно осуществлять по различным направлениям.
Определение. Частным приращением по 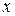 функции
функции  в точке
в точке  соответствующим приращению
соответствующим приращению 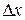 называется разность
называется разность
 .
.
Это приращение по существу является приращением функции одной переменной 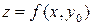 полученной из функции
полученной из функции 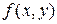 при постоянном значении
при постоянном значении  .
.
Аналогично частным приращением по  в точке
в точке  функции
функции  соответствующим приращению
соответствующим приращению 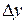 называется разность
называется разность
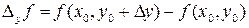 .
.
Это приращение вычисляется при фиксированном значении  .
.
Пример. Пусть 
 ,
,  ,
, 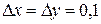 . Найдем частные приращения этой функции по
. Найдем частные приращения этой функции по 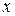 и по
и по 
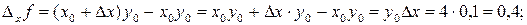
 .
.
В данном примере при равных значениях приращений аргументов 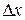 и
и 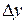 , частные приращения функции оказались различными. Это связано с тем, что площадь прямоугольника со сторонами
, частные приращения функции оказались различными. Это связано с тем, что площадь прямоугольника со сторонами  и
и  при увеличении стороны
при увеличении стороны  на
на  увеличивается на величину
увеличивается на величину 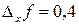 , а при увеличении стороны
, а при увеличении стороны  на
на  увеличивается на
увеличивается на 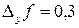 (см.рис.4).
(см.рис.4).

Рис.4.
Из того факта, что функция двух переменных имеет два вида приращений, следует, что для нее можно определить два вида производных.
Определение. Частной производной по 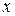 функции
функции  в точке
в точке  называется предел отношения частного приращения по
называется предел отношения частного приращения по 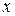 этой функции в указанной точке к приращению
этой функции в указанной точке к приращению 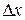 аргумента
аргумента 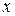 т.е.
т.е.
 . (1)
. (1)
Такие частные производные обозначаются символами  ,
,  ,
, 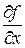 ,
, 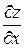 . В последних случаях круглая буква “
. В последних случаях круглая буква “ ” – “
” – “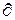 ” означает слово “частная”.
” означает слово “частная”.
Аналогично, частная производная по  в точке
в точке  определяется с помощью предела
определяется с помощью предела
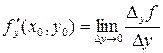 . (2)
. (2)
Другие обозначения этой частной производной:  ,
,  ,
,  .
.
Частные производные функций находятся по известным правилам дифференцирования функции одной переменной, при этом все переменные, кроме той, по которой дифференцируется функция, считаются постоянными. Так при нахождении  переменная
переменная  принимается за постоянную, а при нахождении
принимается за постоянную, а при нахождении 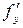 - постоянная
- постоянная 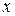 .
.
Пример. Найдем частные производные функции  .
.
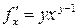 ,
, 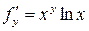 .
.
Пример. Найдем частные производные функции трех переменных
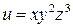 .
.
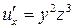 ;
; 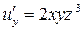 ;
;  .
.
Частные производные функции  характеризуют скорости изменения этой функции в случае, когда одна из переменных фиксируется.
характеризуют скорости изменения этой функции в случае, когда одна из переменных фиксируется.
Пример по экономики.
Основным понятием теории потребления является функция полезности 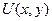 . Эта функция выражает меру полезности набора
. Эта функция выражает меру полезности набора 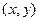 , где х- количество товара Х, у - количество товара У. Тогда частные производные
, где х- количество товара Х, у - количество товара У. Тогда частные производные  будут соответственно называться предельными полезностями х и у. Предельная норма замещения
будут соответственно называться предельными полезностями х и у. Предельная норма замещения одного товара другим равна отношению их предельных полезностей:
одного товара другим равна отношению их предельных полезностей:
 . (8)
. (8)
Задача 1. Найти предельную норму замещения ч на у для функции полезности  в точке А(3,12).
в точке А(3,12).
Решение: по формуле (8) получаем

Экономический смысл предельной нормы замещения заключается в обосновании формулы 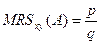 , где
, где  -цена товара Х,
-цена товара Х, 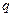 - цена товара У.
- цена товара У.
Определение. Если у функции  имеются частные производные, то ее частными дифференциалами называются выражения
имеются частные производные, то ее частными дифференциалами называются выражения
 и
и 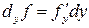
здесь  и
и 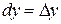 .
.
Частные дифференциалы являются дифференциалами функций одной переменной полученных из функции двух переменных  при фиксированных
при фиксированных  или
или 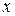 .
.
Примеры из экономики. Рассмотрим в качестве примера функцию Кобба-Дугласа.
Величина  - средняя производительность труда, так как это количество продукции (в стоимостном выражении), произведенное одним рабочим.
- средняя производительность труда, так как это количество продукции (в стоимостном выражении), произведенное одним рабочим.
Величина 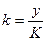 - средняя фондоотдача- количество продукции, приходящееся на один станок.
- средняя фондоотдача- количество продукции, приходящееся на один станок.
Величина  - средняя фондовооруженность- стоимость фондов, приходящееся на единицу трудовых ресурсов.
- средняя фондовооруженность- стоимость фондов, приходящееся на единицу трудовых ресурсов.
Поэтому частная производная  называется предельной производительностью труда, так как она равна добавочной стоимости продукции, произведенной еще одним дополнительным рабочим.
называется предельной производительностью труда, так как она равна добавочной стоимости продукции, произведенной еще одним дополнительным рабочим.
Аналогично, 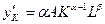 - предельная фондоотдача.
- предельная фондоотдача.
В экономике часто задают вопросы: на сколько процентов изменится выпуск продукции, если число рабочих увеличить на 1% или если фонды возрастут на 1%? Ответы на такие вопросы дают понятия эластичности функции по аргументу или относительная производная. Найдем эластичность выпуска продукции по труду  . Подставляя в числитель вычисленную выше частную производную
. Подставляя в числитель вычисленную выше частную производную 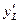 , получим
, получим 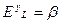 . Итак, параметр
. Итак, параметр 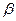 имеет ясный экономический смысл – это эластичность выпуска по труду.
имеет ясный экономический смысл – это эластичность выпуска по труду.
Аналогичный смысл имеет и параметр 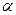 - это эластичность выпуска по фондам.
- это эластичность выпуска по фондам.
Литература
1. Бугров Я.С., Никольский С.М. Дифференциальное и интегральное исчисление, М.:Наука, 1988г.
2. Пискунов Н.С. Дифференциальное и интегральное исчисление для втузов. Т.1,2 М.:Наука, 1985г.
3. Кудрявцев Л.Д. Курс математического анализа. Т. 1,2, М.: Высшая школа, 1981г.
4. Бронштейн И.Н.,Семендяев К.А. Справочник по математике для инженеров.М.: Высшая школа,1997.
5. ИДЗ. Дифференциальное исчисление функции одной переменной. Под редакцией Рябушко А.П., ч.1,2 Минск, «ВШ», 2002г.
|
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 4297; Нарушение авторских прав?; Мы поможем в написании вашей работы!