Показательный закон надежности

Часто длительность времени безотказной работы элемента имеет показательное распределение, функция распределения которого

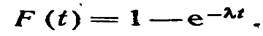
Следовательно, в силу соотношений (*) предыдущего па­раграфа функция надежности в случае показательного распределения времени безотказной работы элемента имеет вид

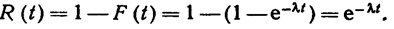
Показательным законом надежности называют функ­цию надежности, определяемую равенством

где λ—интенсивность отказов.

Как следует из определения функции надежности (см. § 4), эта формула позволяет найти вероятность без­отказной работы элемента на интервале времени длитель­ностью t, если время безотказной работы имеет, показа­тельное распределение.

Искомая вероятность того, что элемент проработает безотказно 100 ч, приближенно равна 0,14.

Замечание. Если отказы элементов в случайные моменты времени образуют простейший поток, то вероятность того, что за время длительностью t не наступит ни одного отказа (см. гл. VI, § 6),

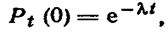
что согласуется с равенством (*), поскольку λ в обеих формулах имеет один и тот же смысл (постоянная интенсивность отказов).

2. Распределение «хи квадрат» и распределение Стьюдента.

Распределение «хи квадрат»

Пусть Χ_i (ί== 1, 2,..., n)—нормальные незави­симые случайные величины, причем математическое ожи­дание каждой из них равно нулю, а среднее квадратическое отклонение—единице. Тогда сумма квадратов этих величин

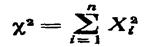
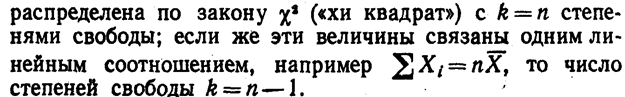
Плотность этого распределения

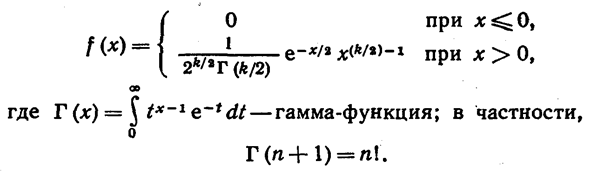
Отсюда видно, что распределение <хи квадрат» опре­деляется одним параметром—числом степеней свободы k.

С увеличением числа степеней свободы распределение медленно приближается к нормальному.

Дата добавления: 2014-01-07