Основные определения. Задачей синтаксического анализа считается проверка, принадлежит ли произвольная заданная цепочка a Î T * языку L(G) для заданной грамматики G

Конечные автоматы

СИНТАКСИЧЕСКИЙ АНАЛИЗ РЕГУЛЯРНЫХ ЯЗЫКОВ

Задачей синтаксического анализа считается проверка, принадлежит ли произвольная заданная цепочка a Î T ^* языку L (G) для заданной грамматики G. На основе методов синтаксического анализа решаются задачи синтаксически управляемой обработки данных (например, текстов). Такой задачей является и задача трансляции. Регулярные языки и порождающие их А-грамматики используются, в основном, для лексического анализа - распознавания в тексте его лексических единиц, лексем, т.е. слов, из которых по более сложным правилам строится текст.

Если язык задан регулярным выражением, то для синтаксического анализа этого языка можно построить его А-грамматику с помощью алгоритма из теоремы 3.8. Для анализа регулярного языка используют устройство, называемое конечным автоматом, которое можно построить по А-грамматике языка.

Конечный автомат состоит из ленты конечной длины, на которой записан текст, и читающей головки, движущейся вдоль ленты слева направо. Автомат в каждый момент находится в каком-то состоянии, которых у него конечное число. На каждом шаге автомат сдвигается на один символ вправо (читает символ) и переходит в новое состояние (которое может совпадать со старым). Новое состояние определяется старым состоянием и прочитанным символом. Если прочитан последний символ, автомат останавливается. Новое состояние может определяться неоднозначно - тогда автомат называется недетерминированным. Для анализа же используются детерминированные автоматы. Автомат сообщает, допустима ли прочитанная цепочка.

Формально, конечным автоматом называется набор A = (Q, T, t, q ₀, F), где
T - текстовый алфавит;
Q - конечное множество состояний, T Ç Q = Æ;
q ₀ Î Q - начальное состояние;
F Í Q - множество заключительных состояний;
t - множество правил перехода, t Í Q ´ T ´ Q.

Правило перехода (q, a, q ') Î t записывается в виде (q, a) ® q ' и означает, что из q автомат может перейти в q ', прочитав символ a.

Конфигурацией автомата называется любая цепочка вида qa, где q Î Q и a Î T ^*, в начальной конфигурации q = q ₀. Отношение перехода ® _A на множестве конфигураций определяется следующим образом:

qаa ® _A q ' a Û (q, a) ® q ' Î t

Если для каждой пары (q, a) имеется не более одного правила перехода, то автомат называется детерминированным. Тогда t называется функцией перехода и t (q, a) = q ', если есть правило (q, a) ® q '.

Определим отношение q - a ® q ', означающее, что состояние q ' достижимо из q на цепочке a Î T ^*, как наименьшее отношение, удовлетворяющее следующим условиям:

1. q - e ® q;

2. q - aa ® q ', если в t есть правило (q, a) ® q " и q "- a ® q '.

Говорят, что цепочка a Î T ^* допускается автоматом A, если на a из начального состояния достижимо какое-нибудь заключительное, т.е. если q ₀- a ® q и q Î F. Множество всех допускаемых автоматом A цепочек называется языком, допускаемым автоматом A и обозначается L (A).

Пример 4.1. Множество идентификаторов допускается автоматом с Q ={ q ₀, q ₁}, F ={ q ₁}, T ={ a,..., z,0,...,9} и правилами

(q ₀, a) ® q ₁,..., (q ₀,z) ® q ₁,
(q ₁, a) ® q ₁,..., (q ₁,z) ® q ₁,
(q ₁,0) ® q ₁,..., (q ₁,9) ® q ₁.


Автомат можно наглядно представлять его диаграммой - помеченным ориентированным графом, вершинами которого являются состояния, помеченные именем или номером состояния, а помеченная дуга q - a ® q ' соответствует правилу (q, a) ® q '. Заключительные состояния будем обозначать двойным кружком. Так, предыдущий автомат представляется диаграммой

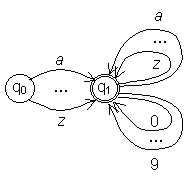
Из определений непосредственно вытекает

Л е м м а 4.1. q - a ® q ' Û в диаграмме есть путь из q в q ', метки дуг которого образуют цепочку a (учитываются и пути нулевой длины, соответствующие a = e).


Дата добавления: 2014-01-07