Парна кореляція і регресія

Часто при аналізі взаємозв’язків соціально-економічних явищ серед різних факторів, що впливають на результат, буває важливо виокремити найбільш значиму факторну ознаку, що більшою мірою обумовлює варіацію результативної ознаки (наприклад, залежність проданих туристичними фірмами путівок від витрат на рекламу або залежність продуктивності праці операторів ЕОМ від стажу роботи). Цим обумовлена ​​необхідність виміру парних кореляцій і побудови рівнянь парних регресій.

Парна регресія дозволяє описати форму зв’язку у вигляді рівняння парної регресії. Основні види рівнянь парної регресії показано в таб. 1.

Таблиця 1

Основні види рівнянь парної регресії

Найменування форми парної регресії	Вид рівняння парної регресії
Лінійна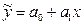
Гіперболічна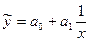
Параболічна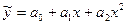
Степенева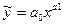

У таблиці позначено:

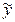– теоретичне значення результативної ознаки (y) при певному значенні факторної ознаки (x), підставленої в регресійне рівняння;

– вільний член рівняння;

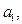
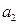– коефіцієнти регресії.

Параметри рівнянь парної регресії 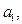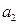називають коефіцієнтами регресії.

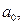
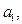
Для оцінки параметрів рівняння парної регресії використовується метод найменших квадратів (МНК). Він полягає у визначенні розподілу параметрів 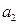при яких сума квадратів відхилень фактичних значень результату від теоретичних () мінімізується. Так, (1) описує вихідну умову МНК для парного лінійного кореляційного зв’язку:

або (1)

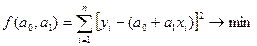
На основі (1) визначаються часткові похідні функції , які потім прирівнюються до нуля. Далі отримані рівняння перетворюються у систему нормальних рівнянь, з яких визначаються параметри 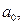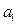. При цьому число нормальних рівнянь у загальному випадку буде дорівнює числу параметрів.

Зокрема, коефіцієнт парної лінійної регресії 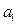визначається відповідно до (2) і характеризує міру зв’язку між варіаціями факторної і результативної ознак. Коефіцієнт регресії показує, на скільки в середньому змінюється значення результативної ознаки при зміні факторної на одиницю:

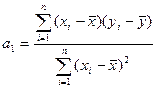, (2)

де n – обсяг сукупності.

Тісноту і напрямок парної лінійного кореляційного зв’язку вимірюють за допомогою лінійного коефіцієнта кореляції (3), що приймає значення в межах від -1 до +1 (табл. 2):

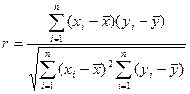. (3)

Квадрат коефіцієнта кореляції називають коефіцієнтом детермінації . Коефіцієнт детермінації можна інтерпретувати як частку загальної дисперсії результативної ознаки (y), яка пояснюється варіацією факторної ознаки (x).

Таблиця 2

Оцінка характеру зв’язку за лінійним коефіцієнтом кореляції

Значення лінійного коефіцієнта кореляції	Характер зв’язку
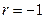
	функціональний
	зворотній сильний
	зворотній помірний
	зворотній слабкий
	відсутній
	прямий слабкий
	прямий помірний
	прямий сильний
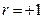
	функціональний

Значимість лінійного коефіцієнта кореляції перевіряється на підставі
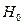t-критерію Ст’юдента: перевіряється нульова гіпотеза про відсутність зв’язку між факторною та результативною ознаками (). Для перевірки за формулою (4) слід розрахувати t-статистику (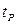) і порівняти її з табличним значенням (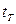) із заданим рівнем значущості (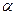) і числом степенів свободи . Якщо 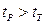, то гіпотеза 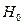відхиляється з імовірністю помилки менше ніж 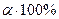. Це свідчить про значущість лінійного коефіцієнта кореляції та статистичної суттєвості залежності між факторною та результативною ознаками.

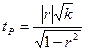, (4)

де k = n -2 для малої вибірки;

k = n при великій кількості спостережень (n >100).

Аналогічно оцінюється значимість коефіцієнта регресії; 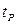розраховують як відношення взятого по модулю коефіцієнта регресії до його середньої помилки з заданими рівнем значущості (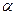) і числом степенів свободи .

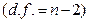Дата добавления: 2014-01-07