Багаторядний (пороговий) алгоритм самоорганізації моделей

Багаторядний алгоритм МГУА

Ідея багаторядного алгоритму ґрунтується на ідеях селективного відбору, застосовуваних біологами при схрещуванні особин для отримання гібридного різновиду із заданими властивостями. Гіпотеза селекції стверджує, що алгоритм масової селекції рослин або тварин являється оптимальним алгоритмом обробки інформації у складних задачах [Івахненко,1982].

Багаторядний алгоритм організовує перегляд моделей зі зростанням складності від одного ряду (покоління) до іншого. В результаті такого перегляду деякі моделі виявляються пропущеними, що, з одного боку скорочує обсяг розрахунків, з іншого – спричиняє неточне визначення моделі оптимального складності. Дійсно, якщо модель оптимальної складності виявилась пропущеною, то багаторядний алгоритм не зможе виявити її як найліпшу.

На першому ряду багаторядного алгоритму формуються усі можливі пари змінних зі вхідних змінних системи і складаються моделі, що містять ці пари змінних (рисунок 1). З усіх моделей першого ряду вибираються декілька ліпших за значенням зовнішнього критерію і тільки вони допускаються до другого ряду. На другому ряді формуються усі можливі пари моделей першого ряду і складаються моделі другого ряду. Якість кожної моделі оцінюється за значенням зовнішнього критерію і декілька найліпших відбираються для наступного ряду і т.д. Нарощування рядів відбувається до тих пір, доки з переходом до наступного ряду відбувається зменшення значення зовнішнього критерію. Модель оптимальної складності вибирається як найліпша у найліпшому ряду.

Рисунок 1. Багаторядний (пороговий) алгоритм самоорганізації моделей

Для того, щоб побудувати багаторядний алгоритм потрібно:

· визначити зовнішній критерій, за яким здійснюється вибір моделі оптимальної складності;

· визначити вид моделі, використовувану для пари змінних на кожному ряду алгоритму;

· визначити спосіб розподілу таблиці даних;

· визначити кількість моделей, що переходять з одного ряду до наступного;

· для кожної моделі ряду визначити параметри моделі і розрахувати значення зовнішнього критерію;

· за значенням зовнішнього критерію вибрати найліпші моделі, що переходять до наступного ряду;

· формувати таблицю даних, що є вихідною таблицею для наступного ряду;

· нарощувати кількість рядів, доки зростання складності моделі призводить до зменшення значення зовнішнього критерію;

· визначити модель оптимальної складності як найліпшу модель найліпшого ряду.

Формування моделей ряду

На першому ряду розглядаються моделі, які використовують вхідні змінні досліджуваної системи по дві змінні:

, (1)

де u, s – пара чисел, 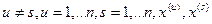- компоненти вектора вхідних змінних х.

В найпростішому випадку, припускають лінійний вид моделей:

(2)

Для кожної моделі (2) за даними частини таблиці даних А відшукуються параметри b.

Вибір найліпших моделей за значенням зовнішнього критерію.

Кожна j -та модель i -ого ряду оцінюється за допомогою зовнішнього критерію, що розраховується з використанням частини таблиці даних В. Позначимо розраховане значення критерію . Найменше значення критерію, досягнуте на даному ряду називається критерієм ряду:

(3)

3 усіх моделей ряду вибирається К штук найліпших за значенням зовнішнього критерію, які переходять у наступний ряд. Інші моделі, які не проявили себе як найліпші, знищуються. Відбір моделей, що переходять до наступного ряду, називається порогом. Число К має бути не меншим за три для того, щоб у наступному ряді існувала можливість сформувати більше однієї моделі.

Формування таблиці даних наступного ряду

Для тих моделей, що виявились найліпшими на першому ряду, формується таблиця даних наступним чином. Значення вхідних змінних пропускаються через найліпші моделі першого ряду і отримуються значення вихідних змінних моделей першого ряду:

Перехід до наступного (j+1) ряду здійснюється за умови, що значення критерію ряду зменшується:

(4)

Іншими словами, доки ускладнення моделі спричиняє поліпшення значення критерію. Якщо значення критерію ряду більше за значення критерію попереднього ряду, то алгоритм зупиняється і відшукується єдина найліпша модель з моделей попереднього ряду. Саме ця модель вважається моделлю оптимальної складності.

Зауважимо, що в багаторядних алгоритмах складність моделі зростає при переході від одного ряду до іншого, оскільки зростає кількість шуканих параметрів. Якщо на першому ряду отримані моделі виду:

То модель другого ряду має вид:

,

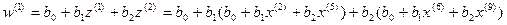де значення коефіцієнтів b в усіх моделях різні, а позначення схематичне(!).

Формування результату пошуку моделі оптимальної складності.

Припустимо, що модель оптимальної складності знайдена на третьому ряду багаторядного алгоритму самоорганізації моделей:

,

де 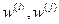- змінні другого ряду.

Залежність змінних другого ряду від змінних першого ряду представляється функціональними залежностями:

, ,

де 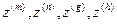- змінні другого ряду.

Нарешті, залежність змінних першого ряду представляється функціональними залежностями від вихідних змінних моделі:

Тому, модель оптимальної складності представляється через вихідні дані наступним чином:

Отже, символьне представлення моделі оптимальної складності, яка знайдена, у багаторядному алгоритмі набагато складніше ніж в однорядному алгоритмі і потребує розробки спеціального алгоритму для виведення результату. Якщо багаторядний алгоритм використовується для прогнозування, то замість виве­дення символьного результату обмежуються чисельним виведенням результатів прогнозу.

На рисунку 2 наведена узагальнена схема багаторядного алгоритму самоорганізації моделей

Рис. 2. Узагальнена схема багаторядного алгоритму самоорганізації моделей

Дата добавления: 2014-01-07