О-нотация

Begin

Подсчет числа простейших операций

В соответствии с методом подсчета простейших операций алгоритм представляется в виде программы на развитом языке программирования (например, Pascal). Определяется множество простейших операций высокого уровня, которые не зависят от языка программирования. К таким операциям относятся:

1) присваивание переменной значения,

2) вызов метода (процедуры или функции),

3) выполнение арифметической операции,

4) сравнение двух значений,

5) индексация массива,

6) переход по ссылке на объект,

7) возвращение из метода.

Данный метод основан на неявном предположении, что время выполнения простейших операций приблизительно одинаково. Таким образом, К простейших операций, выполняемых внутри алгоритма, пропорционально действительному времени выполнения данного алгоритма.

Рассмотрим процесс подсчета простейших операций на примере алгоритма определения максимального значения в одномерном массиве X, состоящего из N элементов. На рисунке 3.2 приводится код данного алгоритма на языке Pascal.

currentMax:= X[0];

for i:= 1 to N-1 do

if currentMax < X[i] then currentMax:= X[i];

end;

Рисунок 3.2 – Pascal-код алгоритма определения максимального значения в массиве

Приведем рассуждения, формулируемые в процессе анализа:

- на этапе инициализации переменной currentMax и присваивания ее значения X[0] выполняются две простейшие операции (индексация массива и присваивание значения); таким образом, счетчик операций равен 2;

- в начале цикла for счетчик i получает значение 1, что соответствует одной простейшей операции присваивания;

- перед выполнением тела цикла проверяется условие i< N (операция сравнения); такое сравнение выполняется N раз, поэтому счетчик простейших операций увеличивается еще на N единиц;

- тело цикла выполняется для значений i, равных 1, 2, …, N -1. При каждой итерации X[i] сравнивается с currentMax (две простейших операции – индексирование и сравнение), значение X[currentMax], возможно, присваивается переменной currentMax (две операции – сложение и присваивание), а счетчик i увеличивается на 1 (две операции – сложение и присваивание). Следовательно, при каждой итерации цикла выполняется 4 или 6 простейших операций, в зависимости от выполнения одного из условий X[i]£ currentMax или X[i]> currentMax. Таким образом, при выполнении тела цикла в счетчик операций добавляется 4(N –1) или 6(N –1);

- при возвращении значения переменной currentMax однократно выполняется одна простейшая операция.

Итак, число простейших операций К(N), выполняемых алгоритмом, минимально равно

,

а максимально

.

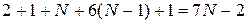Число выполняемых простейших операций равно минимально (К(N) = 5 N) в том случае, если X[0] является максимальным элементом массива, т. е. переменной currentMax не присваивается нового значения. Число выполняемых операций максимально равно 7 N –2 в том случае, если элементы массива упорядочены по возрастанию, и переменной currentMax присваивается значение при каждой итерации цикла.

Для выражения характеристик быстродействия в вычислительной технике используется короткая схема – О -нотация (big-Oh notation). В этой нотации используется специальная математическая функция от N, т. е. количества исходных данных, которому пропорционально быстродействие алгоритма. Утверждается, что алгоритм принадлежит к классу О (f (N)), где f (N) – некоторая функция от N. Приведенное обозначение читается как «О большое от f (N)» или, менее строго, «пропорционально f (N)»

Например, исследования показали, что алгоритм А принадлежит к классу О (N), а алгоритм В – к классу О (log(N)). Поскольку для положительных чисел log(N) < N, можно сделать вывод о том, что алгоритм В всегда эффективнее алгоритма А.

О-нотация подчиняется простым арифметическим правилам. Во-первых, умножение математической функции внутри скобок в О-нотации на константу не оказывает никакого влияния на О-нотацию. Например, О (3 f (N)) и О (24 f (N)) эквивалентно О (f (N)), поскольку константы 3 или 24 можно без последствий вынести за скобки как коэффициент пропорциональности, который игнорируется.

Во-вторых, О-нотация демонстрирует асимптотическое поведение, проявляющееся в том, что для больших значений N О-нотация определяет тот класс алгоритма, к которому принадлежит его доминантная часть. Пусть некоторый алгоритм принадлежит к классу О (N ² + N). Если величина N достаточно велика, то влияние члена «+ N» поглощается членом «N ²». Другими словами при больших значениях N алгоритм О (N ² + N) эквивалентен алгоритму О (N ²). То же можно сказать и для более высоких степеней N.

Предположим, что есть алгоритм, который выполняет три различных задачи. Первая задача выполняется алгоритмом класса О (N), вторая – алгоритмом класса О (N ²), третья – алгоритмом класса О (log(N)). Каково будет быстродействие алгоритма в целом. Ответ будет О (N ²), поскольку к этому классу принадлежит доминантная часть алгоритма.

Таким образом, значения О большого характеризуют алгоритм для больших значений N, а для маленьких значений N О-нотация не имеет смысла.

Дата добавления: 2014-01-07