Else Begin

Begin

Type

Бинарное дерево

9.4.1 Структура бинарного дерева

Упорядоченные деревья второй степени (m -арные деревья при m =2) называют двоичными или бинарнымидеревьями. Упорядоченное бинарное дерево можно определить как множество вершин, которое либо пусто, либо состоит из корня с двумя отдельными двоичными деревьями, которые называют левым и правымподдеревьями этого корня. Деревья степени больше двух называют сильно ветвящимися деревьями (multiway trees).

При представлении бинарного дерева в виде связного списка каждый элемент может содержать поля данных и два структурных указателя: указатель (Left) левого сына и указатель (Right) правого сына. Такое представление называется естественным представлением бинарного дерева.

Тип бинарного дерева (базовый тип дерева) может быть объявлен следующим образом:

Pvertex = ^Tvertex;

Tvertex = Record

Dat: <поля данных>;

Left, Right: Pvertex;

End;

Var CurrentVertex, Root: Pvertex;

CountVertex: Integer;

где Dat, как и ранее, - совокупность информационных полей; Left и Right поля структурных указателей. Поля данных мы будем использовать для размещения меток вершин. Переменные-указатели CurrentVertex и Root и необходимы для идентификации соответственно некоторой текущей вершины и корня. CountVertex - количество вершин в дереве.

На рисунке 9.8 изображена структура естественного представления бинарного дерева (пустые поля указателей содержат пустые ссылки).

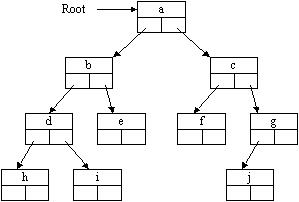
Рисунок 9.8 - Естественное представление бинарного дерева

9.4.2 Формирование бинарного дерева

Предположим, что нужно построить такое бинарное дерево, которое при заданном количестве вершин N имела бы минимальную высоту. Очевидно, минимальная высота дерева достигается, если на всех уровнях, кроме последнего, поместить максимально возможное число вершин. Этого можно добиться, размещая «приходящие» в дерево вершины поровну слева и справа от той вершины, которая будет для них родителем. В результате при каждом увеличении количества вершин мы будем получать деревья, показанные на рисунке 9.9.

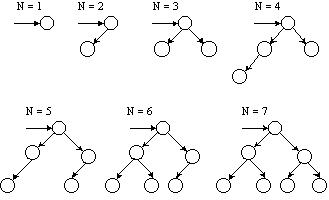
Рисунок 9.9 - Сбалансированные бинарные деревья для различных N

Дерево, имеющее структуру, показанную на рисунке 9.9, называется сбалансированным деревом (balanced tree, AVL-tree). В таком дереве число потомков в левом и правом поддереве любой вершины отличается не более, чем на 1.

Алгоритм формирования сбалансированного бинарного дерева допускает следующую рекурсивную формулировку:

- взять одну вершину в качестве корня;

- построить тем же способом левое поддерево с Nleft = N Div 2 вершинами;

- построить тем же способом правое поддерево с Nright = N - Nleft - 1 вершинами.

Вышеприведенному алгоритму соответствует рекурсивная функция BinaryTreeCreate, приведенная ниже:

Function BinaryTreeCreate(N: Integer): Pvertex;

Var Nleft, Nright: Integer;

If N = 0 Then Tree:= Nil

Nleft:= N Div 2;

Nright:= N - Nleft - 1;

New(CurrentVertex);

BinaryTreeCreate:= CurrentVertex;

With CurrentVertex^ Do Begin

<занесение данных в поля Dat>

Left:= BinaryTreeCreate(Nleft);

Right:= BinaryTreeCreate(Nright);

End;

End;

End;

Для использования функции BinaryTreeCreate нужно передать ей значение числа вершин и выполнить вызов в следующей форме:

Root:= BinaryTreeCreate(CountVertex);

9.4.3 Обход бинарного дерева

Методы обхода дерева любой степени, рассматриваемые в подразделе 10.3, переформулируем в отношении бинарных деревьев.

1) Нисходящий обход:

- обработка корня,

- нисходящий обход левого поддерева,

- нисходящий обход правого поддерева.

Вершины дерева, изображенного на рисунке 9.8, поступали бы на обработку при обходе нисходящим методом в следующем порядке: a, b, d, h, i, e, c, f, g, j.

2) Смешанный обход:

- смешанный обход левого поддерева,

- обработка корня,

- смешанный обход правого поддерева.

Например, при обходе дерева на рисунке 9.8 смешанным методом вершины обрабатываются в следующей последовательности: h, d, i, b, e, a, f, c, j, g.

3) Восходящий обход:

- восходящий обход левого поддерева,

- восходящий обход правого поддерева,

- обработка корня.

Порядок обработки вершин того же дерева при восходящем обходе выглядит так: h, i, d, e, b, f, j, g, c, a.

Для методов обхода в применении к бинарным деревьям часто применяют специфичные названия: нисходящий обход называют обходом pre‑order, смешанный обход - обходом in-order и восходящий - обходом post‑order. Обход post‑order чаще всего применяется для уничтожения всех вершин в бинарном дереве, когда процесс уничтожения можно было бы описать следующим образом: «чтобы уничтожить все вершины бинарного дерева, необходимо уничтожить левое поддерево корня, затем правое поддерево, а затем и сам корень».

Все три метода легко представить рекурсивными процедурами. Прежде чем это сделать, необходимо определить процедуру, активируемую на этапе «обработка». Такая процедура должна выполнять некоторые действия над вершиной, к которой получен доступ на текущем шаге просмотра. А доступ к элементу связной структуры легче всего обеспечить через указатель, который назовем pNode. Текст такой процедуры может выглядеть, например, следующим образом:

Procedure ProcessingNode(pNode: Pvertex);

Var S: String;

Дата добавления: 2014-01-07