Поиск, использующий бинарное дерево

End

Begin

Бинарный поиск

Наиболее эффективным методом поиска в упорядоченном массиве без использования вспомогательных индексов или таблиц является двоичный или бинарный поиск (binary search). Очевидно, что других способов убыстрения поиска не существует, если, конечно, нет еще какой-либо информации о данных, среди которых идет поиск. Другие названия бинарного поиска - поиск делением пополам, дихотомический поиск (dichotomizing search).

Рассмотрим алгоритм бинарного поиска в предположении, что поиск выполняется по первичному ключу. Основная идея - выбрать случайно некоторый элемент, предположим а[m], и сравнить его значение ключа с аргументом поиска ArgSearch. Если а[m].Кey равен ArgSearch, то поиск заканчивается, если он (ключ а[m].Кey) меньше ArgSearch, то мы заключаем, что все элементы с индексами, меньшими или равными m, можно исключить из дальнейшего поиска. Если же он больше ArgSearch, то исключаются индексы больше и равные m. Это соображение приводит нас к алгоритму, программный текст которого приведен ниже. Здесь две индексные переменные L и R отмечают соответственно левый и правый конец секции массива а, где еще может быть обнаружен требуемый элемент.

L:= 0; R:= HighIndex; index:= -1;

While (L<=R) Do

m:= <любое значение между L и R>;

If а[m].Кey = ArgSearch Then Begin

index:= m;

Break

ElseIf a[m].Кey < ArgSearch Then L:= m+1

Else R:= m-1

End;

Выбор m произволен в том смысле, что корректность алгоритма от него не зависит. Однако на его эффективность выбор влияет. Ясно, что наша задача - исключить на каждом шаге из дальнейшего поиска, каким бы ни был результат сравнения, как можно больше элементов. Оптимальным решением будет выбор срединного элемента (т. е. среднего элемента не по значению, а по положению), для чего в вышеприведенном фрагменте следует записать

m:= (L+R) div 2;

При этом в любом случае будет исключаться половина массива. В результате максимальное число сравнений равно значению log₂N, округленному до ближайшего целого. Приведенный алгоритм существенно выигрывает по сравнению с последовательным поиском, ведь там ожидаемое среднее число сравнений равно N/2.

Бинарный поиск может быть использован вместе с индексно-последовательной организацией таблицы, упоминавшейся ранее. Вместо поиска по индексу последовательно может быть использован бинарный поиск. Бинарный поиск может быть также использован при поиске в основной таблице, когда идентифицированы две граничные записи. Однако размер этого сегмента таблицы, вероятно, будет настолько малым, что бинарный поиск не более эффективен, чем последовательный поиск.

Алгоритм бинарного поиска может быть использован только в том случае, если таблица хранится в виде упорядоченного массива. Это происходит потому, что данный алгоритм использует тот факт, что индексами элементов массива являются последовательные целые числа. По этой причине бинарный поиск практически бесполезен в ситуациях, где имеется много добавлений, требующих дополнительного упорядочения элементов, или логических удалений.

Бинарные деревья находят широкое применение для хранения таблицы с тем, чтобы сделать сортировку этой таблицы более эффективной. В этом методе все левосторонние потомки некоторой вершины с ключом Кey имеют ключи, которые меньше ключа Кey, а все правосторонние потомки имеют ключи, которые больше или равны ключу Кey. Смешанный обход такого бинарного дерева дает последовательность, упорядоченную по возрастающему значению ключа. Такое дерево может также быть использовано для бинарного поиска, поэтому оно называется деревом бинарного поиска (binary search tree).

Допустим, имеется следующая последовательность ключей:

30, 47, 85, 95, 115, 130, 138, 159, 166, 184, 206, 212, 219, 224, 237, 258, 296, 307, 314

Дерево бинарного поиска, соответствующего этой последовательности, показано на рисунке 10.3.

Алгоритм поиска в дереве бинарного поиска использует упорядоченность дерева. Поиск элемента выполняется следующим образом. Поиск начинается с корневой вершины, и эта вершина становится текущей. Затем аргумент поиска сравнивается с ключом текущей вершины. Если они равны, то требуемый элемент найден. В противном случае, если аргумент поиска меньше ключа текущей вершины, то выполняется переход к левой дочерней вершине, которая становится текущей. Если аргумент поиска больше ключа текущей вершины, то необходимо перейти к правому сыну текущей вершины, который станет текущей вершиной. В любом случае после перехода к новой вершине происходит этап сравнения ключа с аргументом поиска. Со временем либо определяется нужная вершина, либо достигается лист дерева, что свидетельствует об отсутствии искомого элемента в дереве.

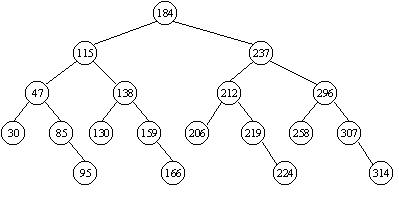
Рисунок 10.3 - Бинарное дерево поиска

Бинарный поиск, рассмотренный ранее, фактически использует отсортированный массив как некоторое неявное дерево бинарного поиска. Срединный элемент этого массива можно представить как корень такого дерева, нижнюю половину массива (все те элементы, которые меньше, чем срединный элемент) можно рассматривать как левое поддерево, а верхнюю половину (все те элементы, которые больше, чем срединный элемент) - как правое поддерево.

Упорядоченный массив может быть получен из дерева бинарного поиска при помощи смешанного обхода этого дерева и вставки каждого элемента последовательно в некоторый массив по мере того, как он встречается в дереве. С другой стороны, для некоторого заданного отсортированного массива имеется много соответствующих ему деревьев бинарного поиска. Предпочтительными являются сбалансированные бинарные деревья, рассмотренные в п. 9.4.2, для которых среднее время, затрачиваемое на поиск, пропорционально log₂N.

Дата добавления: 2014-01-07