Общие сведения и определения

Хеширование и хеш-таблицы

End

Else Begin

End

Repeat

Begin

up:= true; p:= 1;

h:= 1; m:= N;

If up Then Begin i:= 1; j:= N; k:= N+1; l:= 2*N End

Else Begin k:= 1; l:= N; i:= N+1; j:= 2*N End;

Repeat {слияние серий из i и j в k}

If m>=p Then q:= p Else q:= m;

m:= m-q;

If m>=p Then r:= p Else r:= m;

m:= m-r;

While (q<>0) And (r<>0) Do Begin {слияние}

If a[i].Key < a[j].Key Then Begin

a[k]:= a[i]; k:= k+h; i:= i+1; q:= q-1

a[k]:= a[j]; k:= k+h; j:=j-1; r:=r-1

End;

{копирование остатка серии из j}

While r<>0 Do Begin

a[k]:= a[j]; k:= k+h; j:= j-1; r:= r -1

End;

{копирование остатка серии из i}

While q<>0 Do Begin

a[k]:= a[i]; k:= k+h; i:= i+1; q:= q-l

End;

h:= -h; t:= k; k:= l; l:=t

Until m=0;

up:= -up; p:=2*p;

Until p>=n

If -up Then For i:=1 To N Do a[i]:=a[i+N];

End; {Mergesort}

Алгоритм сортировки прямым слиянием выдерживает сравнение даже с усовершенствованными методами внутренней сортировки. Но затраты на управление индексами довольно высоки, кроме того, существенным недостатком является использование памяти размером 2N элементов. Поэтому сортировка слиянием редко применяется при работе с массивами, т. е. данными, расположенными в оперативной памяти.

11.3.2 Сортировка естественным слиянием

В случае простого слияния мы ничего не выигрываем, если данные уже частично рассортированы. На k-м проходе длина всех сливаемых последовательностей меньше или равна 2^k. При этом не учитывается то, что более длинные последовательности могут быть уже упорядочены и, следовательно, их можно сливать. Фактически можно было бы сразу сливать какие-либо упорядоченные подпоследовательности длиной m и k в одну последовательность из m+k элементов. Метод сортировки, при котором каждый раз сливаются две самые длинные возможные подпоследовательности, называется естественным слиянием.

Упорядоченную подпоследовательность часто называют цепочкой. Но, поскольку слово «цепочка» чаще используется для обозначения односвязного списка, мы будем использовать слово серия, когда речь идет об упорядоченной подпоследовательности. Сортировка естественным слиянием сливает последовательности не фиксированной длины, а серии. Серии имеют то свойство, что при слиянии двух последовательностей, каждая из которых содержит n серий, возникает одна последовательность, содержащая ровно n /2 серий. Таким образом, на каждом проходе общее число серий уменьшается вдвое, и число необходимых пересылок элементов в худшем случае равно N×log₂N, а в обычном случае даже меньше. Ожидаемое число сравнений, однако, намного больше, так как кроме сравнений, необходимых для упорядочения элементов, требуются еще сравнения соседних элементов каждого файла для определения концов серии.

Пусть исходная последовательность элементов задана в виде файла а, который в конце работы должен содержать результат сортировки. Используются две вспомогательные ленты b и с. Каждый проход состоит из фазы распределения, которая распределяет серии поровну из а в b и с, и фазы слияния, которая сливает серии из b и с в а. В качестве примера ниже показан файл а в исходном состоянии (строка 1) и после каждого прохода (строки 2 - 4). В естественном слиянии участвуют 20 чисел. Заметим, что требуются только три прохода. Сортировка заканчивается, как только число серий в а будет равно 1. (Предполагается, что в исходном файле имеется хотя бы одна непустая серия.)

17, 31, | 05, 59, | 13, 41, 43, 67, | 11, 23, 29, 47, | 03, 07, 71, | 02, 19, 57, | 37, 61

05, 17, 31, 59, | 11, 13, 23, 29, 41, 43, 47, 67, | 02, 03, 07, 19, 57, 71, | 37, 61

05, 11, 13, 17, 23, 29, 31, 41, 43, 47, 59, 67, | 02, 03, 07, 19, 37, 57, 61, 71

02, 03, 05, 07, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 57, 59, 61, 67, 71

Схематично процесс сортировки естественным слиянием можно отобразить рисунком 11.7.

Рисунок 11.7 - Фазы сортировки естественным слиянием

При просмотре последовательности, выполняемом на фазе разделения (распределения) определяется конец очередной серии. Элемент, расположенный на конце предыдущей серии должен быть больше первого элемента следующей серии, т. е. нужно сравнивать ключи двух последовательных элементов. Однако природа последовательности такова, что непосредственно доступен только один-единственный элемент. Поэтому невозможно избежать «заглядывания вперед», т. е. необходимо считывать в некий «буфер» первый еще не считанный элемент последовательности.

Процесс сравнения и выбора ключей при слиянии заканчивается, как только исчерпана одна из двух серий. После этого оставшаяся неисчерпанной серия должна быть просто передана в результирующую серию, т.е. скопирована в ее «хвост».

11.3.3 Сортировка многопутевым слиянием

Затраты на любую последовательную сортировку пропорциональны числу требуемых проходов, так как по определению при каждом из проходов копируются все данные. Один из способов сократить это число – распределять серии в более чем две последовательности (ленты).

Допустим, исходная последовательность хранится на ленте а. Кроме того, используются r дополнительных лент: b₁, b₂ , …, b_r. Тогда r- путевое слияние выполняется следующим образом: первая серия на ленте а распределяется на ленту b₁, вторая - на ленту b₂ и т. д., r-ая серия - на ленту b_r; затем (r+1)-ая серия на ленту b₁, (r+2)-ая - на ленту b₂ и так до тех пор, пока не распределится последняя из серий ленты а. Затем начальные серии всех дополнительных лент, сливаются на ленту а в одну общую серию, вторые серии дополнительных лент сливаются во вторую серию на ленту а и т. д. Подобный процесс может быть представлен схемой, показанной на рисунке 11.8.

Рисунок 11.8 - Схема r-путевого слияния

Таким образом, естественное слияния является 2‑х путевым слиянием.

Слияние p серий поровну распределенных в r последовательностей (лент) даст в результате p/r серий. Второй проход уменьшит это число до р/r², третий – до р/r³ и т. д., после k проходов останется r/p^k серий. Поэтому общее число проходов, необходимых для сортировки N элементов с помощью r-путевого слияния, равно k=log_rN. Поскольку в каждом проходе выполняется N операций копирования, то в самом плохом случае понадобится N×log_rN таких операций.

На практике многопутевое слияние реализуется как сбалансированное многопутевое слияние с одной единственной фазой, которое предполагает, что в каждом проходе участвует равное количество входных и выходных файлов (лент), в которые по очереди распределяются последовательные серии. Такой алгоритм использует r лент (r - четное число), поэтому он базируется на (r/2)-путевом слиянии. Фазы разделения и слияния как бы объединяются в одну фазу, в ходе которой серии из r/2 лент, называемых входными, не сливаются в одну общую последовательность, а тут же разделяются на другие r/2 лент (они называются выходными), после чего входные и выходные последовательности меняются местами.

11.3.4 Многофазная сортировка

В основе усовершенствований, реализованных в многофазной сортировке (Polyphase Sort), лежит отказ от жесткого понятия прохода и переход к более изощренному использованию последовательностей, называемых лентами. Этот метод был изобретен Р. Гилстэдом.

Продемонстрируем многофазную сортировку на примере с тремя последовательностями (лентами) f1, f2 и f3. В каждый момент сливаются элементы из двух лент-источников и записываются в третью ленту. Как только одна из входных последовательностей исчерпывается, она сразу же становится выходной для операции слияния из оставшейся, неисчерпанной входной последовательности и предыдущей выходной.

Поскольку известно, что p серий на каждом из входов трансформируются в p серий на выходе, то нужно только держать список из числа серий в каждой последовательности (а не определять их действительные ключи). Будем считать, что в начале две входные последовательности f1 и f2 содержат соответственно 13 и 8 серий. Следовательно, на первом проходе 8 серий из f1 и f2 сливаются в f3, на втором – 5 серий из f1 и f3 и сливаются в f2 и т. д. В конце концов, в f1 оказывается отсортированная последовательность. Этот процесс показан на рисунке 11.9.

Рисунок 11.9 - Многофазная сортировка слиянием 21 серии на трех лентах

Многофазная сортировка более эффективна, чем сбалансированная многопутевая, поскольку она имеет дело с (r-1)-путевым слиянием, а не с (r/2)-путевым слиянием, если она начинается с r последовательностей (лент). Ведь число необходимых проходов приблизительно равно log_rN, где N – число сортируемых элементов, а r – степень операции слияния, – это и определяет значительное преимущество многофазной сортировки.

В разделе 10 были рассмотрены алгоритмы поиска элемента в таблице. Эти алгоритмы предполагают, что прежде, чем найти требуемую запись, необходимо организовать просмотр и сравнение с аргументом поиска некоторого количества ключей. Организация таблицы (последовательная, индексно-последовательная, в виде бинарного дерева и т. д.) и порядок, в котором вставляются ключи, определяют то число ключей, которое должно быть проверено до получения нужного ключа. Очевидно, что эффективными методами поиска являются те методы, которые минимизируют число этих проверок. Было показано, что наиболее эффективным методом поиска является бинарный поиск, требующий в наихудшем случае выполнения числа сравнений, приблизительно равного log₂N. Однако бинарный поиск не может быть применен для таблиц с произвольным расположением элементов: элементы должны быть расположены в отсортированном порядке.

В идеале мы бы хотели иметь такую организацию таблицы, при которой не было бы ненужных сравнений. Посмотрим, возможна ли такая организация. Если каждый ключ должен быть извлечен за один доступ, то положение записи внутри такой таблицы может зависеть только от данного ключа. Оно не может зависеть от расположения других ключей, как это имеет место в дереве. Наиболее эффективным способом организации такой таблицы является одномерный массив, т. е. доступ к каждой записи обеспечивается с помощью ее уникального целочисленного индекса, который определяет позицию элемента в общей таблице. Если ключи записей являются целыми числами, то сами ключи могут использоваться как индексы в массиве. Рассмотрим пример такой системы.

Предположим, что некоторая фирма-производитель имеет таблицу с перечнем производимых изделий, состоящую из 1000 наименований изделий, причем каждое изделие имеет уникальный номенклатурный номер из трех цифр. Тогда обычным способом хранения этой таблицы является описание некоторого массива:

a[0], a[1], a[2], …, a[HighIndex].

Допустим для определенности, что массив a описывается нотациями (11.1) и (11.2). Общее число элементов по‑прежнему обозначаем N, тогда HighIndex = N - 1.

В нашем случае можно задать N = 1000, и если номера изделий, составляющие содержимое поля Key, являются ключами, то целесообразно определить, что эти номера используются как индексы в данном массиве. Тогда запись с ключом, например, 67 при вставке размещается в элементе a[67]. В такой таблице легко организовать поиск: элемент, соответствующий аргументу поиска ArgSearch, - это элемент a[ArgSearch]. Мы видим, что при такой организации таблицы при поиске не нужно производить ни одного сравнения.

Та же самая структура может использоваться для организации файла производимых изделий, даже если на складах фирмы накопилось до, например, 200 наименований изделий (при условии что ключи по-прежнему состоят из трех цифр). Хотя многие ячейки в массиве a тогда бы соответствовали несуществующим ключам, эти потери компенсируются преимуществом прямого доступа к записи с информацией о каждом из существующих изделий.

К сожалению, такая система не всегда имеет практический смысл. Например, предположим, что фирма имеет некоторую таблицу производимых изделий, состоящую из более 1000 пунктов, и ключ каждой записи является номером изделия из семи цифр. Для применения прямой индексации с использованием полного семизначного ключа потребовался бы массив из 10000000 (10 млн.) элементов. Ясно, что это привело бы к потере неприемлемо большого пространства памяти, поскольку совершенно невероятно, что какая-либо фирма может иметь больше чем несколько тысяч наименований изделий. Поэтому необходим некоторый метод преобразования ключа в какое-либо целое число внутри ограниченного диапазона. В идеале в одно и то же число не должны преобразовываться два различных ключа. К сожалению, такого идеального метода не существует. Попытаемся разработать методы, которые приближаются к идеальным, и определить, какие действия надо предпринять, когда идеальный случай не достигается.

Рассмотрим опять пример с таблицей наименований изделий фирмы, в которой каждая запись задается ключом из семизначного номера изделия. Предположим, что фирма имеет не более 1000 наименований изделий и что для каждого изделия используется только одна запись. Тогда для хранения всего файла будет достаточно массива из 1000 элементов. Этот массив индексируется целым числом в диапазоне от 0 до 999 включительно. В качестве индекса записи об изделии в этом массиве используются три последние цифры номера изделия. Это показано на рисунке 12.1. Отметим, что два ключа, которые близки друг к другу как числа (такие как 4618396 и 4618996), могут располагаться дальше друг от друга в этой таблице, чем два ключа, которые значительно различаются как числа (такие как 0000991 и 9846995). Это происходит из-за того, что для определения позиции записи используются только три последние цифры ключа.

Функция, которая трансформирует ключ в некоторый индекс в таблице, называется функцией хеширования (hash function). Другие названия функции хеширования: хеш-функция, функция перемешивания. Если h является некоторой хеш-функцией, а Кey некоторый ключ, то h(Кey) называется значением хеш-функции от ключа Кey и является индексом, по которому должна быть помещена запись с ключом Кey. Преобразование ключа элемента в значение индекса называется хешированием (hashing). Массив, используемый для хранения элементов, в котором индексы определяются с помощью хеширования ключей, называется хеш-таблицей (hash table).

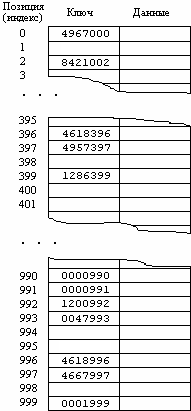
Рисунок 12.1 - Размещение записей в таблице, когда
позиция записи определяется по трем последним цифрам ключа

Если мы обозначим остаток от деления X на Y как X Mod Y, то хеш‑функция для вышеприведенного примера есть

h(Кey) = Кey Mod 1000. (12.1)

Значения, которые выдает функция h, должны покрывать все множество индексов в таблице. Например, функция Кey Mod 1000 может дать любое целое число в диапазоне от 0 до 999 в зависимости от значения Кey. Как мы вскоре увидим, хорошей идеей является таблица, размер которой немного больше, чем число вставляемых записей. Это иллюстрируется на рисунке 12.1, где несколько позиций таблицы не используются.

Дата добавления: 2014-01-07