Опытно-конструкторские работы

Под опытно—конструкторскими работами понимается применение результатов прикладных исследований для создания образцов новой техники, материала, технологии. Опытно-конструкторские работы — это завершающая стадия научных исследований, переход от лабораторных условий и экспериментального производства к промышленному производству.

К опытно-конструкторским работам относятся:

эскизно-техническое проектирование;

выпуск рабочей проектно-конструкторской документации, в том числе чертежи на детали, сборочные соединения, изделие в целом;

изготовление и испытание опытных образцов;

разработка определённой конструкции инженерного объекта или технической системы;

разработка идей и вариантов нового объекта;

разработка технологических процессов;

определение наименования продукта, товарного знака, маркировки, упаковки.

Выделяются четыре уровня общности исследований:

общеотраслевой уровень значимости – работы, результаты которых оказывают воздействие на всю область той или иной науки;

дисциплинарный уровень значимости характеризует исследования, результаты которых вносят вклад в развитие отдельных научных дисциплин, входящих в научную область;

общепроблемный уровень значимости имеют исследования, результаты которых изменяют существующие научные представления по ряду важных проблем внутри одной дисциплины.

частнопроблемный уровень значимости характеризует исследования, результаты которых изменяют научные представления по отдельным частным вопросам.

Исследования по цели их проведения можно разделить на несколько типов:

поисковые;

критические;

уточняющие;

воспроизводящие.

К первому типу относятся поисковые исследования. Хотя название звучит тавтологично, под ним подразумевается попытка решения проблемы, которую никто не ставил или не решал подобным методом. Иногда аналогичные исследования называют исследованиями "методом тыка": "Попробуем так, может что-то и получится". Научные работы такого рода направлены на получение принципиально новых результатов в малоисследованной области.

Второй тип -критические исследования. Они проводятся в целях опровержения существующей теории, модели, гипотезы, закона и пр. или для проверки того, какая из двух альтернативных гипотез точнее прогнозирует реальность. Критические исследования проводятся в тех областях, где накоплен богатый теоретический и эмпирический запас знаний и имеются апробированные методики для осуществления эксперимента.

Большинство исследований, проводимых в науке, относится к уточняющим исследованиям. Их цель - установление границ, в пределах которых теория предсказывает факты и эмпирические закономерности. Обычно, по сравнению с первоначальным экспериментальным образцом, изменяются условия проведения исследования, объект, методика. Тем самым регистрируется, на какую область реальности распространяется полученное ранее теоретическое знание.

И, наконец, последний тип - воспроизводящее исследование. Его цель - точное повторение эксперимента предшественников для определения достоверности, надежности и объективности полученных результатов. Результаты любого исследования должны повториться в ходе аналогичного эксперимента, проведенного другим научным работником, обладающим соответствующей компетенцией. Поэтому после открытия нового эффекта, закономерности, создания новой методики и т. п. возникает лавина воспроизводящих исследований, призванных проверить результаты первооткрывателей' Воспроизводящее исследование - основа всей науки

Сформировав замысел предстоящей работы и определив ее направленность, исследователь приступает к выявлению научного противоречия.

Противоречие– это «взаимодействие между взаимоисключающими, но при этом взаимообусловливающими и взаимопроникающими друг в друга противоположностями внутри единого объекта и его состояний...».

Такое толкование противоречия в строгом смысле, как правило, применимо к «точным» наукам, например, к физике.

В качестве классических иллюстраций противоречий можно привести противоречия, сложившиеся в конце ХIХ в.: между принципом относительности Г. Галилея и системой уравнений Д. Максвелла в электродинамике, которое было разрешено созданной А. Эйнштейном специальной теорией относительности.

Выявленное исследователем противоречие может иметь место в практике или в теории науки, может быть целый ряд противоречий. Кроме того, неполнота исследованности предметной области является свидетельством неполноты теории, то есть наличия противоречия – несоответствия теории соответствующей предметной области.

На основе выявленного противоречия исследователь ставит для себя проблему исследования.

Под научной проблемой понимается такой вопрос, ответ на который не содержится в накопленном обществом научном знании. проблема – это специфическая форма организации знания, объектом которого является не непосредственная предметная реальность, а состояние научного знания об этой реальности.

Если мы знаем, что нам неизвестно что-то об объекте, например, какие-либо его проявления или способы связи между его какими-то компонентами, то мы уже имеем определенное проблемное знание.

Например, мы четко знаем, что до конца не известна природа шаровой молнии. Здесь налицо знание о незнании. Оно лежит в основе выдвижения научных проблем.

В процессе постановки проблемы выделяют следующие этапы: формулирование, оценка, обоснование и структурирование проблемы.

1. Постановка проблемы. В процессе формулирования проблемы важное значение имеет постановка вопросов. Постановка проблемы есть, прежде всего, процесс поиска вопросов, которые, сменяя друг друга, приближают исследователя к наиболее адекватной фиксации неизвестного и способов превращения его в известное.

Но постановка проблемы не исчерпывается этим моментом. Во-первых, не всякий научный вопрос есть проблема – он может оказаться всего лишь уточняющим вопросом, или вопросом, вообще неразрешимым для науки на сегодняшний день.

Во-вторых, для постановки проблемы недостаточно вопроса. Требуется еще выявление оснований данного вопроса.

Приведем такой интересный пример фиксации противоречия, лежащего в основе научной проблемы. Для того, чтобы много знать и уметь, надо иметь хорошую память и тренированное мышление. И здесь мы встречаемся с неизбежным противоречием: отдать больше времени накоплению знаний – значит меньше оставить времени на тренировку мышления, и наоборот. А раз так, следовательно, есть какой-то оптимум. Если бы его удалось установить, отпали бы многие сложности.

Важное значение для формулирования проблемы имеет построение образа, «проекта» ожидаемого конечного результата исследования на основе прогноза развития исследования и «фона» данной проблемы. Под «фоном» понимаются все обстоятельства, с которыми связана на данном этапе, а также будет связана в дальнейшем, проблема и которые оказывают и будут оказывать влияние на ход и результаты исследования.

2. Оценка проблемы. В оценку проблемы входит определение всех необходимых для ее решения условий, в число которых в зависимости от характера проблемы и возможностей науки входит определение методов исследования, источников информации, состава научных работников, организационных форм, необходимых для решения проблемы, источников финансирования, видов научного обсуждения программы и методик исследования, а также промежуточных и конечных результатов, перечня необходимого научного оборудования, необходимых площадей и т.д.

3. Обоснование проблемы. Обоснование проблемы – это, во-первых, определение содержательных, ценностных и генетических связей данной проблемы с другими – ранее решенными и решаемыми одновременно с данной, а также выяснение связей с проблемами, решение которых станет возможным в зависимости от решения данной проблемы.

Во-вторых, обоснование проблемы – это поиск аргументов в пользу необходимости ее решения, научной или практической ценности ожидаемых результатов. Это необходимость сравнивать данную с другими с учетом важности каждой из них для потребностей практики и внутренней логики науки.

При этом современная наука часто имеет дело с проблемами, допускающими несколько вариантов решения. В том числе, например, в современной российской экономике появилось многообразие моделей различных фирм, подходов к организации бизнеса и т.д. В таких случаях приходится детально обосновывать, какое именно решение, какая именно модель обладает наибольшими преимуществами и поэтому более желательна в данных условиях.

Чем сложнее проблема, тем большее количество разнородных факторов необходимо учитывать при обосновании ее разрешимости и планировании ее решения. Умение ученого формулировать и критически анализировать аргументы, используемые для обоснования разрешимости или принятия предлагаемого решения проблемы, является в таких условиях важной предпосылкой прогресса науки.

При оценке значимости проблемы нередко можно встретиться с переоценкой ее действительной значимости. В связи с этим у ученых вырабатывается защитная реакция: действительную значимость любой проблемы они склонны рассматривать в гораздо меньших масштабах, чем авторы научных трудов, где раскрываются эти проблемы. Это вполне естественное для науки явление.

Наука должна быть в меру консервативна и не должна кидаться в крайности по поводу любой новой работы любого нового автора. Но, в то же время, иногда это приводит к недооценке важных проблем и неоправданной задержке развития новых направлений в науке. Например, то, что произошло с генетикой и кибернетикой в начале 50-х годов ХХ века – по этим направлениям советская наука была отброшена на десятилетия назад.

Для снижения субъективности оценки проблемы важное значение имеет выдвижение, как самим исследователем, так и его коллегами, всевозможных возражений против проблемы.

Под сомнение ставится все, что относится к существу проблемы, условиям постановки и следствиям ее разрешения: есть ли проблема? Имеется ли практическая или научная потребность в ее разрешении?

Возможно ли ее разрешение при современном состоянии науки? Посильна ли эта проблема данному исследователю или данному научному коллективу? Какова возможная ценность планируемых результатов?

4. Структурирование проблемы. Исходным пунктом структурирования проблемы является ее расщепление, или «стратификация» проблемы. Расщепление (декомпозиция – поиск дополнительных вопросов (подвопросов), без которых невозможно получить ответ на центральный проблемный – вопрос. В исходной позиции редко можно сформулировать все подвопросы проблемы. Это происходит в значительной мере в ходе самого исследования.

«Наука ищет пути всегда одним способом, – писал В.И. Вернадский, – она разлагает сложную задачу на более простые, затем, оставляя в стороне сложные задачи, разрешает более простые и только тогда возвращается к оставленной сложной».

Далее, в процессе расщепления проблемы необходима ее локализация – ограничение объекта изучения реально обозримыми и посильными для исследователя или исследовательского коллектива пределами с учетом наличных условий проведения исследования.

Постановка проблемы осуществляется всегда с использованием средств какого-то научного языка. Избранные для выражения проблемы понятия и структуры языка далеко не индифферентны ее смыслу. Нередки случаи, когда непонимание учеными друг друга было связано не со сложностью самих проблем, а с неоднозначным употреблением терминов.

Поставив проблему своего исследования, исследователь определяет его предметную область (напомним, что предметная область – это вся совокупность явлений, описываемых данной теорией).

У исследователя, взявшегося за такое обобщающее исследование, появляются многочисленные разнородные и разноаспектные результаты, которые трудно объединить в единое целое.

Начинается длительный поиск – какая же предметная область, какая же формулировка темы, какая концепция могут объединить, собрать воедино все наработанные результаты или, по крайней мере, их бoльшую часть. Ведь нередко бывает, что часть результатов никак не ложится в единое русло и их приходится отбрасывать. В то же время подчас оказывается, что чего-то из необходимых результатов недостает, и исследование следует продолжить. Здесь будет уместно привести такую аналогию из теории множеств

Представим себе, что имеются отдельные разрозненные результаты – «множества» – 1, 2, 3, 4 и т.д. (см. Рис. 6а). Они могут частично «перекрывать» друг друга. Задача состоит в том, чтобы найти такое общее множество -объединяющее множество (см. Рис. 6б), которое вберет в себя все или, по крайней мере, большую часть отдельных множеств. Подчас отдельные результаты, не относящиеся к определенной конечной предметной области, приходится отбрасывать (на Рис. 6б – это множества 8 и 9).

Попробуем описать примерный «алгоритм» этого поиска.

Представим себе три условные плоскости: плоскость предметных областей; плоскость методов и средств познания – условно назовем их общим названием «технологии» (познания); плоскость результатов.

Новые результаты могут быть получены:

1. Либо тогда, когда исследована новая, ранее не изученная предметная область (Рис. 7а);

2. Либо к ранее исследованной предметной области применены новые технологии – методы или средства познания (Рис. 7б); например, к исследованию какой-либо предметной области применен новый исследовательский подход, или применена какая-либо теория из другой области научного знания, или применен какой-либо математический аппарат (в роли средства познания), ранее не применявшийся к исследованию данной предметной области, или применены новые материальные средства – например, новые приборы либо новые языковые средства и т.д.;

3. Либо одновременно исследуется новая предметная область с использованием новых технологий (Рис. 7в). Интересно, что в некоторых отраслях науки исследователей принято подразделять на две категории. Одних условно называют «гаечниками» (они как бы «отворачивают гайки» – исследуют новые предметные области). Других – «ключниками» (они применяют новые технологии познания, то есть «подбирают новые ключи для отворачивания гаек»). Исследователь должен четко определить для себя – какой из этих вариантов соответствует его замыслу и наработанным результатам.

4. Еще один вариант (Рис. 7г), очевидно, принципиально невозможен – нельзя получить новые результаты, сделать крупные обобщения, рассматривая уже изученную предметную область и используя прежние технологии.

Можно выделить следующую закономерность – чем шире предметная область, тем сложнее получать для нее общие научные результаты. В математике этот эффект проявляется наиболее ярко: любое формальное утверждение (например, теорема) состоит из двух частей – предположений («Пусть...») и результата (вывода: «Тогда...»).

Чем более сильные предположения (условия) – иначе говоря, ограничения – вводятся, тем проще доказать один и тот же результат, или тем более глубокие результаты можно получить. При минимальных (слабых) предположениях (условиях, ограничениях) получаются наиболее слабые результаты. И наоборот – чем более сильный результат необходим, тем больше ограничивающих предположений, как правило, приходится вводить.

Таким образом, существует определенный «баланс» между вводимыми предположениями и получаемыми результатами. «Прорывом» в математике (да и в других науках, существенно использующих формальный аппарат) является либо получение более общих (новых) результатов при существующих (или более слабых) предположениях, либо ослабление предположений, при которых остаются справедливыми известные выводы.

Различные варианты определения предметной области обобщающего исследования

Вернемся к более подробному описанию различных вариантов определения предметной области обобщающего исследования. Здесь можно попробовать подвести определенную типологию.

Воспользуемся опять аналогией из теории множеств – диаграммами Эйлера-Венна

Случай а). Отдельное множество (аналог – новая предметная область). Данный вариант – появление абсолютно новой предметной области – встречается достаточно редко (обычно исследователь, в силу своего образования, принадлежности научной школе «зашорен»), однако именно этот вариант может привести к революционному появлению новых научных направлений;

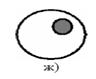
Случай б). Одно множество включено в другое множество (аналог – расширение предметной области). Наверное, это– наиболее типичный случай эволюционного развития некоторой теории, научной школы: предметная область расширяется за счет расширения предмета исследований, обобщения полученных результатов и т.д. В математике, например, этот случай соответствует ослаблению вводимых предположений с сохранением полученных результатов, или получению новых более общих результатов в рамках существующих предположений;

Случай в). Объединение множеств (аналог – предметная область образуется на общих элементах двух предметных областей). Типичный пример обобщения, когда появляется теория, объединяющая две пересекающиеся по предметным областям теории. Данный случай (также, как и случай б) обычно характерен для эволюционного развития, но может отражать и революционные моменты развития теории (все зависит от размера предметных областей).

Примером из физики является созданная в 60-е годы XX века Янгом и Миллсом теория электрослабого взаимодействия, описывающая с единых позиций электромагнитное и слабое взаимодействия;

Случай г). Пересечение множеств (аналог – предметная область образуется на общих элементах двух предметных областей). Данный случай соответствует либо получению (за счет сужения предметной области) более глубоких результатов, чем были получены в соответствующих предметных областях (что представляется достаточно экзотическим), либо переносу результатов (обычно – методов исследования – см. Рис. 7в) из одной предметной области в другую, или содержательным интерпретациям результатов, полученных в одной предметной области, в терминах другой предметной области.

Примером является успешное применение в начале XX века достаточно развитого к тому времени аппарата дифференциальных уравнений (используемых до тех пор, в основном, в физике и технике) к описанию экосистем – динамике взаимодействия биологических популяций, конкуренции биологических видов и т.д.;

Случай д). Разность множеств (аналог – предметная область образуется на исключении из одной предметной области элементов другой предметной области);

Случай е). Симметрическая разность множеств (аналог – предметная область образуется на непересекающихся элементах двух предметных областей).

Случаи д) и е) содержательно соответствуют ограничению предметной области, когда в качестве предмета исследования выбираются, например, объекты, обладающие либо только заданным свойством и обязательно не обладающие другим свойством (вариант д) или обладающий одним и только одним из двух свойств (вариант е).

Например, исследуется процесс адаптации индивидуума после ухода на пенсию (исходные множества в случае д) – множество пенсионеров и множество работающих; затенено множество неработающих пенсионеров). Примером для случая е) служит медико-биологическое исследование сравнительной эффективности двух различных лекарств при лечении определенного заболевания. При этом исключается случай одновременного применения обоих лекарств;

Случай ж). Сужение множества (аналог – из предметной области извлекается некоторая совокупность элементов, обладающих вполне определенными одинаковыми свойствами – как новая предметная область). Ситуация типична для наук сильной версии, когда существующие результаты усиливаются за счет введения более сильных (ограничивающих) предположений.

Например, для алгебраических уравнений произвольного порядка существуют численные методы поиска их решения. Для более узкой предметной области, включающей уравнения порядка не выше третьего, существуют аналитические методы решения.

Случай з). Два непересекающихся множества. К этому случаю будут относиться, очевидно, сравнительные исследования. Например, сравнительное исследование законодательств Франции и России.

Поскольку мы рассмотрели способы построения предметных областей, соответствующие по аналогии всем базовым операциям над множествами, можно предполагать, что этим набором операций и их возможными комбинациями исчерпываются все возможные способы определения предметных областей. Таким образом, при проведении обобщающего исследования на установленной предметной области определяется объект и предмет исследования.

Дата добавления: 2014-01-07