Случай воздействия внешних сил в одной плоскости

Внутренние силовые факторы (ВСФ)

Рассмотрим брус длины l, нагруженный внешними силами F₁, F₂,… Для простоты рассмотрим случай, когда силы действуют лишь в плоскости yz (в плоскости листа).

Главный способ анализа напряженного состояния бруса в интересующем нас сечении заключается в том, что тело считается состоящим из двух частей.

Рис.3.1.

Разделим брус, изображенный на рис. 3.1, сечением A на две части. Напомним, что систему координат связывают с этим сечением и вводят по следующим правилам.

1) Система координат вводится в рассматриваемом сечении, а начало координат располагается в центре тяжести сечения.

2) Ось z направляется вдоль оси бруса, оси x и y располагают в плоскости сечения по правилу правого винта.

3) Положение сечения может определяться каким-либо параметром (например, расстоянием s на рис.3.1).

Для простоты будем использовать термин «правая часть бруса». Согласно рис.3.1, это та часть, которая находится со стороны конца оси z, (другую часть будем называть «левой частью бруса»). На эту правую часть бруса воздействует левая часть бруса через внутреннее сечение А силами F₃, F₄ и моментом F₃ s относительно оси x. Эти воздействия (т.е. силы и момент) называются внутренними силовыми факторами.

Таким образом, воздействие одной части бруса на другую называется внутренним силовым фактором. Это определение можно записать как правила вычисления ВСФ (они имеют следующие специальные названия и обозначения).

Сумма внешних сил, действующих на внутреннее сечение слева (или справа) в продольном направлении, носит название продольной силы N_z (синонимы – нормальная сила, осевая сила, усилие растяжения или сжатия).

Сумма внешних сил, действующих на внутреннее сечение слева (или справа) поперек оси бруса (в направлении оси у), называется поперечной силой Q_у. (синоним - перерезывающая сила Q_у.).

Сумма моментов относительно оси х, которые создают внешние силы слева (или справа) отсечения называется изгибающим моментом.

Правила знаков. Отметим еще раз, что они в сопромате весьма специфичны. Для приведенной на рис. 3.1 системы координат их можно ввести следующим образом.

1) Вклад внешней силы в суммарную продольную силу N_z положителен, если эта внешняя сила действует вдоль оси бруса на сечение растягивающим образом (независимо от направления оси z).

В нашем случае слева на сечение воздействует 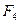, а справа F₁. Поэтому .

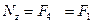2) Если внешняя сила действует слева на сечение поперек оси, то вклад этой внешней силы в суммарную поперечную силу Q_у положителен при совпадении направлений оси у и внешней силы.

В нашем случае слева на сечение воздействует . Поэтому .

Примечание. В силу закона Ньютона, действие правой части должно быть равно действию левой. Поэтому при подсчете N_z, Q_у и слева, и справа должны получаться одни и те же значения. Однако второе правило знаков приходится формулировать по другому, а именно следующим образом: если внешняя сила F действует на сечение справа и его направление совпадает с направлением оси у, то вклад внешней силы во поперечную силу Q_у будет отрицателен. Поскольку в силу условий равновесия бруса в целом имеем равенство F₂ = F₃ , то легко убедиться, что при подсчете Q_у и слева, и справа получатся одни и те же значения..

3) Правило знаков для изгибающих моментов: изгибающий момент 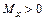, если он, изгибая брус, создает положительную кривизну бруса. Например, в выбранной системе координат это правило для М_х можно представить графически в виде, приведенном на нижеследующем рисунке.

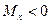
В нашем случае:

Примечания.

1. Если рассматривать воздействие левой части бруса на правую, то правило знаков для моментов М_х совпадает с правилом, вводимым в теоретической механике.

2. Для начала рекомендуется находить ВСФ, рассматривая действие только левой части бруса на правую, или наоборот - только правой части бруса на левую.

3.Часто вместо координаты s, определяющей положение сечения, используют обозначение z. Если ось бруса прямолинейна, то это не вызывает недоразумений. В случае, например, криволинейного кругового бруса положение сечения определяют угловой координатой. При этом необходимо помнить, что ось z направлена перпендикулярно нормальному сечению бруса и проходит через его центр тяжести.

3.2. Основные соотношения между погонной силой q, поперечной силой Q_y и изгибающим моментом M_x

Эти соотношения важны с двух точек зрения.

1) Они позволяют контролировать правильность построения эпюр ВСФ

2) Они нужны при выводе некоторых формул, например, формул вычисления касательных напряжений при изгибе.

Рассмотрим диск толщины ds, вырезанный из балки:

Согласно определению на левое сечение с левой стороны действуют .

Аналогично, справа действует почти такая же сила и момент, поскольку толщина диска бесконечно мала. Так как они мало отличаются от воздействий с левой стороны, то согласно принятым в математике обозначениям это будут силы .

Связь между найдем из соотношений статики. Выпишем первое уравнение равновесия: .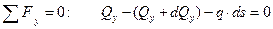

Отсюда вытекает соотношение, называемое первым уравнением равновесия элемента балки

(3.1)

Выпишем второе уравнение равновесия:

Деля на ds получим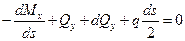

Отсюда следует соотношение, называемое вторым уравнением равновесия элемента балки

(3.2)

Следствие: Согласно теореме Ферма там, где производная меняет знак, функция экстремальна. Поэтому там, где 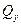меняет знак, изгибающий момент 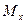экстремален.

Дата добавления: 2014-01-07