Статически неопределимая железобетонная колонна

Расчет статически неопределимых систем

Примеры использования законов механики для расчета строительных сооружений

Рассмотрим бетонную колонну с металлической арматурой, нагруженную через жесткую плиту силой F (рис.9.1). Примем следующие исходные данные (они приняты таковыми только для демонстрации метода отыскания внутренних сил).

Рис.9.1

Дано:

Найти: Силу сжатия бетона и силу сжатия арматуры .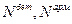

Решение: Возьмем сечение:

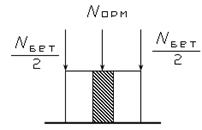
Рис.9.2

На это сечение сила давления F распределяется не одинаково, хотя суммарно имеет место равенства:

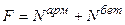- (9.1)

Здесь знак «-» поставлен потому, что имеет место сжатие сечения. Уравнение (9.1) имеет бесконечное множество решений. Уравнений равновесия для однозначного определения сил сжатия бетона и арматуры записать не удается. Поэтому задача называется статически неопределимой. Поскольку методами теоретической механики выбрать решение, отвечающее реальности, невозможно, то для этого используем свойство тел деформироваться, т.е. кинематические соображения и закон Гука. Из рисунка рис.9.1 видно, что и бетон, и арматура укорачиваются одинаково, т.е.

Это соотношение называется уравнением совместности деформации.

Подставим сюда закон Гука.

.

Найдем соотношение знаменателей:

.

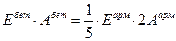Тогда получим:

.

Отсюда

.

Подставляя в (9.1) найдем:

.

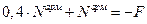Отсюда:

Вывод: хотя арматуры в колонне в два раза меньше чем бетона, но она воспринимает основную часть нагрузки (а именно - 71% нагрузки).

Дата добавления: 2014-01-07