Теория накопления микроповреждений

В любом теле существуют микротрещины и микропоры. Под нагрузкой c течением времени эти микротрещины возрастают в размерах.

Через некоторое время их размеры достигают критических величин, после чего начинается неудержимый рост трещины, и разделение тела на части.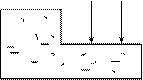

На основе анализа экспериментов были выявлены законы развития микротрещин (теорию накопления повреждений разработал Работнов Ю. Н). Эта теория позволяет определить время, в течение которого конструкция выдерживает внешнюю нагрузку без разрушения. Это время 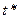назем критическим временем.

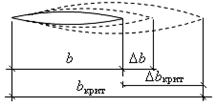
Рассмотрим трещину, длины 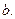Пусть 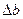- приращение трещины, 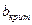- длина микротрещины при котором начинается неудержимый её рост.

Введем параметр поврежденности:

.

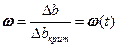1) В начале: 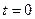, в теле 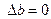, тогда:

При 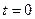, 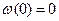(9.7.1)

2) В момент разрушения при 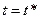: 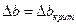, значит при ,

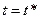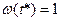(9.7.2)

9.7.1– начальное условие,

9.7.2– условие разрушения.

Закон подрастания трещины, предложенный Работновым Ю.Н. имеет следующий вид:

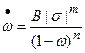(9.7.3)

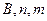- механические характеристики материала.

Процедура вычисления 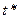состоит из следующих этапов:

1) Определяется напряжение в конструкции в каком-то сечении

2) После подстановки в закон (9.7.3) решается дифференциальное уравнение (9.7.3).

3) Из начального условия (9.7.1) находятся константы интегрирования

4) Из условия прочности (9.7.2) находится критическое время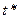

Рассмотрим примеры.

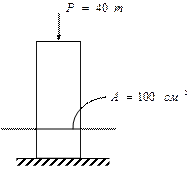
Пример №1: Задача о бетонной колонне

Найдем напряжение:

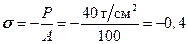т/см².

Пусть известен закон (9.7.3). Пусть 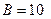см²/век×т, m=1, n=1. Тогда:

.

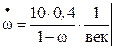Отсюда получаем: .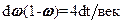

Слева и справа одинаковые функции, значит и первообразные от них равны, или отличаются на константу.

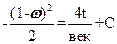(9.7.4)

Константу С найдем из начального условия:

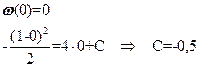(9.7.5)

Теперь (9.7.4) примет вид

.

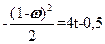Найдем критическое время t* для колонны (ее долговечность) из условия (9.7.2). Подставляя 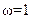в (9.7.5.) получаем:

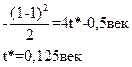
Итак, колонна простоит 12,5 лет

Пример №2:

Задача о накоплении повреждений в железобетонной колонне с учетом ползучести.

С течением времени ввиду релаксации (отдыха) бетона все большую часть нагрузки начинает воспринимать арматура.

То есть, напряжения в бетоне стремятся к нулю. Таким образом, если не учесть накопления повреждений, то напряжение в бетоне уменьшается и его разрушение никогда не наступит.

Однако, это не так. Решим задачу о разрушении колонны в результате накопления повреждений.

Ранее было найдено: .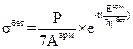

Перепишем в новых обозначениях:

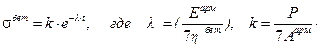
Закон (9.7.3) примет теперь вид:

.

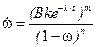Получили обыкновенное дифференциальное уравнение, которое легко решается

Пусть B=10 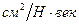, m=n=1.

Тогда получим: .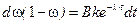

Легко проверить, что решение этого уравнения можно записать в виде:

.

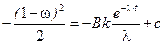Константу с находим из начального условия при t = 0:

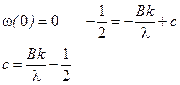
В момент разрушения 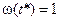. Из этого условия находим уравнение для t*:

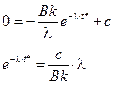
Логарифмируя обе части, получим:

.

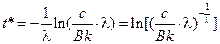Если 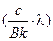< 0, то логарифма не существует. Это значит, что не существует t *, то есть, бетон успеет отрелаксировать и не разрушиться. Если 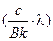> 0, то можно найти критическое время t *, по достижении которого произойдет разрушение колонны.

Дата добавления: 2014-01-07