Расчет сооружений при циклическом нагружении по теории развивающихся трещин

Циклическая нагрузка приводит к развитию трещин во времени. Из экспериментов выявлено, что скорость подрастания трещины тем больше, чем больше размах напряжения растяжения и чем больше длина трещины.

Обозначим через 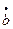- скорость подрастания трещины, то есть:

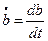(14.2)

Итак, 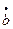тем больше, чем больше размах напряжения растяжения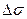и чем больше длина трещины b. Это утверждение можно записать в виде:

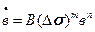(14.3)

Здесь В, m, n – механические характеристики материала.

Эксперименты показывают, что для всех материалов степень n в два раза меньше чем m, т.е.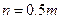

Тогда:

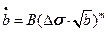(14.4)

Это соотношение называется законом роста трещины.

Если напряжение изменяется во времени, т.е. 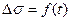, то закон запишется в виде:

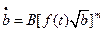(14.5)

Это дифференциальное уравнение относительно длины трещины b. Оно решается методом разделения переменных:

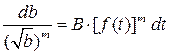(14.6)

Отсюда получим:

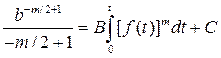(14.7)

Константу С определяют из начальных условий, т.е. из условия, что в начальный момент длина трещины известна. Пусть при t = 0 начальная длина трещины равна b ₀. Тогда

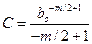(14.8)

Рассмотрим случай, когда можно считать, что размах напряжения постоянен, то есть

f (t) = const=Δ σ_o.

Из(14.7) вытекает выражение

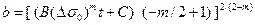(14.9)

Таким образом, в любой момент времени можно вычислить длину трещины.

Согласно формуле Гриффитса, зная длину трещины можно найти предел прочности 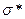, при котором произойдет разрушение:

.

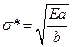Здесь Е модуль Юнга, а - механическая характеристика материала.

Подставляя найденную длину трещины b в условие разрушения 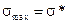, получаем уравнение для отыскания времени разрушения t ^*:

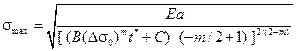(14.10)

Отсюда находим t ^*:

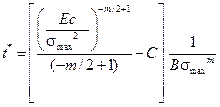
Еще раз отметим, что константы Е, m, а, В являются механическими характеристиками материала, 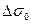- размах напряжения растяжения элемента, константа С определяется по формуле (14.8), в которой 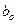- первоначальная длина трещины.

Уменьшая t * на коэффициент запаса k, получаем [ t ] - допустимое значение времени эксплуатации сооружения.

15. Изгиб балок

Дата добавления: 2014-01-07