Формула Мора для вычисления прогиба

Пусть необходимо найти прогиб точки В, т.е. перемещение v_B. (рис.16.2)

Рис. 16.2.

Для решения задачи используем применим закон сохранения энергии в варианте принципа возможных перемещений. В качестве возможных выберем прогиб (здесь и далее величины, характеризующие основную задачу будут снабжаться индексом q).

Рассмотрим фиктивную задачу (рис.16.3)

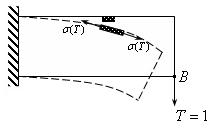
Рис. 16.3.

Вычислим работу силы 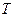на перемещении :

.

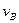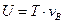Согласно закона сохранения энергии эта работа должна равняться работе внутренних сил. Подсчитаем её.

Рассмотрим рис.16.2 и рис.16.3. Выделим малый элемент балки (он зачернен на рис 16.2 и рис.16.3). Он удлиняется на величину .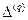

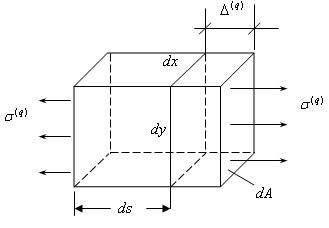
Рис. 16.4.

Рассмотрим этот же малый элемент под действием напряжений растяжения 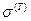(здесь и далее величины, характеризующие фиктивную задачу, будут снабжаться индексом Т), которые возникают, под действием силы Т. Вычислим 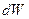- работу этих напряжений на перемещении :

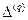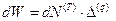
Согласно определению:

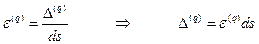
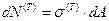
Таким образом,

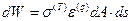
Здесь 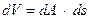– объем малого элемента.

Работа по удлинению всех элементов балки будет:

.

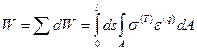В случае балки имеем:

.

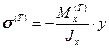По закону Гука:

.

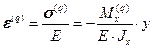Отсюда:

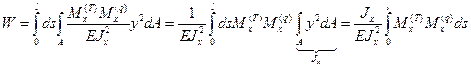
Запишем закон сохранения энергии:

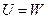
Отсюда вытекает формула Мора:

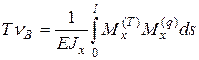(16.2)

Здесь 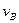- искомый прогиб в точке B (от рабочих нагрузок);

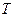=1 – единичная сила, приложенная в интересующем нас направлении искомого прогиба 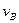в интересующей нас точке В.

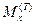- изгибающий момент в фиктивной задаче о приложении к балке силы Т в точке В.

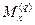- изгибающий момент от рабочих нагрузок.

Физический смысл формулы Мора заключается в следующем: работа силы Т на искомом перемещении v_В равна работе внутренних сил, вызванных этой силой, на деформациях от внешних сил.

Примечания.

1. Работой касательных напряжений 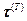обычно пренебрегают ввиду ее малости по сравнению с W.

2. При необходимости вычисления угла наклона балки α вместо единичной фиктивной силы Т необходимо прикладывать единичный момент m в интересующей нас точке. Формула Мора примет вид

.

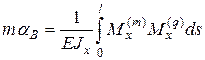Дата добавления: 2014-01-07