Применение теории предельного равновесия для расчета

Задача изгиба балки

Предельный момент.

Рассмотрим балку, которая изгибается силами Р.

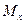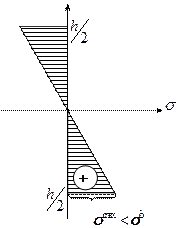
Сделаем сечение I-I. На него справа действует . Нарисуем эпюру при разных значениях М_х. Увеличивая, 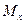достигаем состояния, при котором .

Дальнейшее увеличение 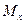приведет к тому, что нижние и верхние волокна будут пластически деформироваться при постоянном

Увеличение 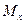в дальнейшем приведет к тому, что по всей высоте волокна перейдут в пластическое состояние. Геометрически это означает, что в данном сечении изгиб балки будет не плавным, а сосредоточенным.

Это состояние в сечении называется предельным, сечение называют пластическим шарниром (пластический излом), а момент, который его вызывает, также называется предельным. Обозначают его 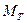(момент текучести).

Подсчитаем его значение. Как обычно разбиваем сечение на малые площадки. Тогда:

,

.

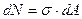В нашем случае 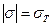. Следовательно:

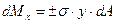
Подсчитаем момент для верхней части сечения:

.

Здесь 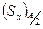- это статический момент верхней половины сечения. Для нижней части получим то же самое. В результате находим:

(21.1.)

Рассмотрим пример отыскания разрушающей силы для статически неопределимой балки (т.е. необходимо найти ).

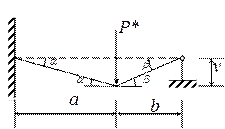Разрушение произойдет тогда, когда под силой и в заделке произойдет пластический излом.

Это означает, что под силой и в заделке момент достигает предельного значения .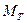

найдем из закона сохранения энергии.

Работа силы будет

.

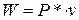Здесь v – это прогиб под силой (см. рисунок).

Эта работа тратится на создание пластических шарниров в заделке и под силой. Подсчитаем работу, которую совершает в них момент .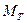

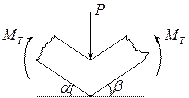
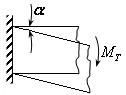
В заделке момент повернул стержень на угол 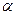, тогда он совершает работу:

.

Рассмотрим теперь малый элемент под силой Р.

Тогда:

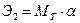
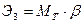
Закон сохранения дает:

,

.

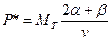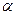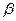Выразим и через .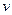

Так как перемещения малы, то , .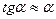

Значит: , .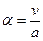

Тогда: .

Подставляя, получаем:

Дата добавления: 2014-01-07