Влияние различных факторов на движение жидкости

Потери напора при установившемся движении.

Кинематика жидкости существенно отличается от кинематики твёрдого тела. Если отдельные частицы абсолютно твёрдого тела жёстко связаны между собой, то в движущейся жидкой среде такие связи отсутствуют; эта среда состоит из множества частиц, движущихся одна относительно другой.

Скорость в данной точке пространства, занятого движущейся жидкостью, является функцией координат этой точки, а иногда и времени.

Рассмотрим движение идеальной жидкости, т.е. такой воображаемой жидкости, которая совершенно лишена вязкости. В такой не вязкой жидкости, так же как и в неподвижных реальных жидкостях, возможен лишь один вид напряжений - нормальные напряжения сжатия, т.е. гидромеханическое давление, или просто давление.

Давление в движущейся идеальной жидкости обладает теми же свойствами, что и в неподвижной жидкости, т.е. на внешней поверхности жидкости оно направлено по внутренней нормали, а в любой точке жидкости - по всем направлениям одинаково.

Течение жидкости может быть установившемся (стационарным) и неустановившемся (нестационарным).

Установившемся называется течение жидкости, неизменное по времени, при котором давление и скорость являются функциями только координат, но не зависят от времени. Давление и скорость могут изменяться при перемещении частицы жидкости из одного положения в другое, но в данной неподвижной относительно русла точке давление и скорость при установившемся движении не изменяются по времени, т.е.:

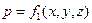
(1.46)

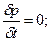
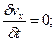
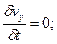
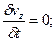(1.47)

где индексы у скорости означают её проекции на соответствующие оси, жёстко связанные с руслом.

Неустановившемся движением называется движение у которого все характеристики изменяются по времени в точках рассматриваемого характера.

При неустановившемся течение траектории различных частиц, проходящих через данную точку пространства, могут иметь разную форму. Поэтому для рассмотрения картины течения, возникающей в каждый данный момент времени, вводится понятие линии тока.

Линией тока называется кривая, в каждой точке которой вектор скорости в данный момент времени направлен по касательной.

Если в движущейся жидкости взять бесконечно малый замкнутый контур и через все его точки провести линии тока, то образуется трубчатая поверхность, называемая трубкой тока. Часть потока, заключённая внутри трубки тока, называется элементарной струйкой.

Живым сечением, или просто сечением потока, называется в общем случае поверхность в переделах потока, проведённая нормально к линиям тока. Далее будем рассматривать в потоках такие участки, в которых струйки можно считать параллельными и, следовательно, живые сечения - плоскими.

Различают напорные и безнапорные течения жидкости. Напорными называют течения в закрытых руслах без свободной поверхности, а безнапорными - течения со свободной поверхностью. При напорных течениях давление вдоль потока обычно переменное, при безнапорном - постоянное (на свободной поверхности) и чаще всего атмосферное.

Дата добавления: 2014-01-07