Распределение скоростей по живому сечению в цилиндрической трубе при ламинарном режиме. Коэффициент Дарси при ламинарном течении

Если боковая поверхность трубы есть поверхность цилиндра, то естественно допустить существование ламинарного течения с линиями тока в виде прямых, параллельных образующим цилиндра.

Для отыскания скорости имеем уравнение Пуассона с постоянной правой частью

(1.67)

граничным условием которого является равенство нулю скорости не стенке трубы.

В общем случае рассматриваемое течение может быть обусловлено как перепадом давления 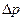, так и осевым движением одного из цилиндров (речь идёт о рассмотрении цилиндрической трубы, состоящей из двух цилиндров (рис. 1.20)).

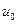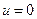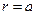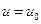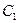Допустим, что внутренний цилиндр перемещается в направлении оси z со скоростью . Такому движению соответствуют граничные условия при , при . Использовав их для определения постоянных и 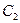, найдём

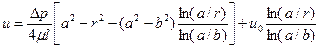(1.68)

рис. 1.20 Цилиндрическая труба из двух цилиндров

В частном случае, если перепада давления нет, то получим осесиммитричное течение Куэтта с распределением скоростей

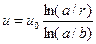
и касательными напряжениями в слое жидкости

,

где .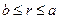

Из этой формулы следует, что если зазор между цилиндрами 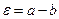мал, то касательные напряжения в слое жидкости могут быть весьма значительными.

При неподвижных цилиндрах () имеем течение в кольцевой трубе с распределением скоростей

(1.69)

Эта зависимость позволяет вычислить все другие характеристики течения. В частности, расход

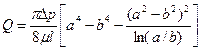(1.70)

Разделив расход на площадь 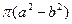кольца, найдём выражение для средней скорости

, (1.71)

которое позволяет вычислять падение давления в кольцевой трубе.

Потери напора при ламинарном течении также находятся по формуле Вейсбаха-Дарси:

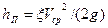, (1.72)

где 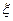- безразмерный коэффициент пропорциональности, называемый коэффициентом потерь Дарси или коэффициентом сопротивления.

Дата добавления: 2014-01-07