Неопределенность, количество информации и энтропия

Бит

Данные

Данными называют информацию, когда делают акцент на том, что она поступает в качестве входных параметров некоторого алгоритма обработки. Данные – от слова “дано”, так же как в записи условия задачи мы записываем “дано” и “найти”.

Этот термин часто употребляется, когда речь идет о компьютерных системах. Одни и те же данные, записанные в компьютерной памяти, могут быть отображены в зависимости от выбранной программы обработки или как графическая информация, или как символьная, или как звуковая, или как числовая.

Данные – это любые зарегистрированные сигналы. Слово “информация” чаще используется в более узком смысле, чем просто все, что отражается в материальном объекте в результате воздействия на него другого материального объекта. Предполагается, что получение информации дает получившему ее возможность принимать решения, действовать, осуществлять выбор или пополнить (и/или реструктурировать) свою систему знаний. Если полученные данные не приводят ни к чему из перечисленного, то с субъективной точки зрения считается, что для получателя они информации не несут, хотя и занимают определенный объем его памяти.

Говоря об информации и ее свойствах, обычно имеют в виду один из трех аспектов:

Технический - точность, надежность, скорость передачи сигналов, объем, занимаемый в памяти зарегистрированными сигналами, способы регистрации сигналов. В этом аспекте информация = данные, и никак не учитывается ее полезность для получателя или ее смысловое содержание. Это информация в самом широком общем для всей материи смысле, информация в аспекте восприятия, хранения, передачи.

Прагматический - насколько эффективно информация влияет на поведение получателя. В этом аспекте говорят о полезности и ценности информации. В определенных случаях ценность информации становится отрицательной, а сама информация становится дезинформацией. Это информация в аспекте управления поведением.

Семантический - передача смысла с помощью кодов. Семантической называется информация, активизирующая образы, уже имеющиеся в тезаурусе получателя (узнаваемая) или вносящая изменения в его тезаурус (систему знаний). Это информация в аспекте знаний.

Раздел 3. Количество информации

По определению А. Д. Урсула - «информация есть отраженное разнообразие». Количество информации есть количественная мера разнообразия. Это может быть разнообразие совокупного содержимого памяти; разнообразие сигнала, воспринятого в процессе конкретного сообщения; разнообразие исходов конкретной ситуации; разнообразие элементов некоторой системы… - это оценка разнообразия в самом широком смысле слова.

Любое сообщение между источником и приемником информации имеет некоторую продолжительность во времени (длину сообщения), но количество информации воспринятой приемником в результате сообщения, характеризуется в итоге вовсе не длиной сообщения, а разнообразием сигнала порожденного в приемнике этим сообщением.

Память носителя информации имеет некоторую физическую ёмкость, в которой она способна накапливать образы, и количество накопленной в памяти информации, характеризуется в итоге именно разнообразием заполнения этой ёмкости. Для объектов неживой природы это разнообразие их истории, для живых организмов это разнообразие их опыта.

Однообразные пейзажи снежных или песчаных пустынь – отраженное однообразие температурного режима, разнообразие средней полосы – отражение разнообразия ее природных факторов.

Разнообразие человеческого опыта, отражается в мироощущении: однообразие сужает кругозор, разнообразие – расширяет. Сидение в четырех стенах сужает мир до размера квартиры, наличие в квартире телевизора – расширяет мир до размеров планеты. Тяга к путешествиям, общению, новым знакомствам, новому опыту, новым ощущениям это тяга к получению новых, ранее не известных впечатлений в память, новых образов, следовательно, новой информации.

Разнообразие необходимо при передаче информации. Нельзя нарисовать белым по белому, одного состояния недостаточно. Если ячейка памяти способна находиться только в одном (исходном) состоянии и не способна изменять свое состояние под внешним воздействием, это значит, что она не способна воспринимать и запоминать информацию. Информационная емкость такой ячейки равна 0.

Минимальное разнообразие обеспечивается наличием двух состояний. Если ячейка памяти способна, в зависимости от внешнего воздействия, принимать одно из двух состояний, которые условно обозначаются обычно как «0» и «1», она обладает минимальной информационной ёмкостью.

Информационная ёмкость одной ячейки памяти, способной находиться в двух различных состояниях, принята за единицу измерения количества информации - 1 бит.

1 бит (bit - сокращение от англ. bi nary digi t - двоичное число) - единица измерения информационной емкости и количества информации, а также и еще одной величины – информационной энтропии, с которой мы познакомимся позже. Бит, одна из самых безусловных единиц измерения. Если единицу измерения длины можно было положить произвольной: локоть, фут, метр, то единица измерения информации не могла быть по сути никакой другой.

На физическом уровне бит является ячейкой памяти, которая в каждый момент времени находится в одном из двух состояний: «0» или «1».

Если каждая точка некоторого изображения может быть только либо черной, либо белой, такое изображение называют битовым, потому что каждая точка представляет собой ячейку памяти емкостью 1 бит. Лампочка, которая может либо «гореть», либо «не гореть» также символизирует бит. Классический пример, иллюстрирующий 1 бит информации – количество информации, получаемое в результате подбрасывания монеты – “ орел ” или “ решка ”.

Количество информации равное 1 биту можно получить в ответе на вопрос типа «да»/ «нет». Если изначально вариантов ответов было больше двух, количество получаемой в конкретном ответе информации будет больше, чем 1 бит, если вариантов ответов меньше двух, т.е. один, то это не вопрос, а утверждение, следовательно, получения информации не требуется, раз неопределенности нет.

Информационная ёмкость ячейки памяти, способной воспринимать информацию, не может быть меньше 1 бита, но количество получаемой информации может быть и меньше, чем 1 бит. Это происходит тогда, когда варианты ответов «да» и «нет» не равновероятны. Неравновероятность в свою очередь является следствием того, что некоторая предварительная (априорная) информация по этому вопросу уже имеется, полученная, допустим, на основании предыдущего жизненного опыта. Таким образом, во всех рассуждениях предыдущего абзаца следует учитывать одну очень важную оговорку: они справедливы только для равновероятного случая.

Количество информации мы будем обозначать символом I, вероятность обозначается символом P. Напомним, что суммарная вероятность полной группы событий равна 1.

Основоположенник теории информации Клод Шеннон определил информацию, как снятую неопределенность. Точнее сказать, получение информации - необходимое условие для снятия неопределенности. Неопределенность возникает в ситуации выбора. Задача, которая решается в ходе снятия неопределенности – уменьшение количества рассматриваемых вариантов (уменьшение разнообразия), и в итоге выбор одного соответствующего ситуации варианта из числа возможных. Снятие неопределенности дает возможность принимать обоснованные решения и действовать. В этом управляющая роль информации.

Представьте, что вы зашли в магазин и попросили продать вам жевательную резинку. Продавщица, у которой, скажем, 16 сортов жевательной резинки, находится в состоянии неопределенности. Она не может выполнить вашу просьбу без получения дополнительной информации. Если вы уточнили, скажем, - «Orbit», и из 16 первоначальных вариантов продавщица рассматривает теперь только 8, вы уменьшили ее неопределенность в два раза (забегая вперед, скажем, что уменьшение неопределенности вдвое соответствует получению 1 бита информации). Если вы, не мудрствуя лукаво, просто указали пальцем на витрине, - «вот эту!», то неопределенность была снята полностью. Опять же, забегая вперед, скажем, что этим жестом в данном примере вы сообщили продавщице 4 бита информации.

Ситуация максимальной неопределенности предполагает наличие нескольких равновероятных альтернатив (вариантов), т.е. ни один из вариантов не является более предпочтительным. Причем, чем больше равновероятных вариантов наблюдается, тем больше неопределенность, тем сложнее сделать однозначный выбор и тем больше информации требуется для этого получить. Для N вариантов эта ситуация описывается следующим распределением вероятностей: {1/N, 1/N, … 1/N}.

Минимальная неопределенность равна 0, т.е. эта ситуация полной определенности, означающая что выбор сделан, и вся необходимая информация получена. Распределение вероятностей для ситуации полной определенности выглядит так: {1, 0, …0}.

Величина, характеризующая количество неопределенности в теории информации обозначается символом H и имеет название энтропия, точнее информационная энтропия.

Энтропия (H) – мера неопределенности, выраженная в битах. Так же энтропию можно рассматривать как меру равномерности распределения случайной величины.

Рис. 8. Поведение энтропии для случая двух альтернатив.

На рисунке 8. показано поведение энтропии для случая двух альтернатив, при изменении соотношения их вероятностей (p, (1-p)).

Максимального значения энтропия достигает в данном случае тогда, когда обе вероятности равны между собой и равны ½, нулевое значение энтропии соответствует случаям (p₀=0, p₁=1) и (p₀=1, p₁=0).

Количество информации I и энтропия H характеризуют одну и ту же ситуацию, но с качественно противоположенных сторон. I – это количество информации, которое требуется для снятия неопределенности H. По определению Леона Бриллюэна информация есть отрицательная энтропия (негэнтропия).

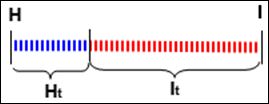
Рис. 9. Связь между энтропией и количеством информации.

Когда неопределенность снята полностью, количество полученной информации I равно изначально существовавшей неопределенности H.

При частичном снятии неопределенности, полученное количество информации и оставшаяся неснятой неопределенность составляют в сумме исходную неопределенность. H_t + I_t = H.

По этой причине, формулы, которые будут представлены ниже для расчета энтропии H являются и формулами для расчета количества информации I, т.е. когда речь идет о полном снятии неопределенности, H в них может заменяться на I.

Дата добавления: 2014-01-07