Математические модели с использованием сетей Петри

Сети Петри являются эффективным инструментом дискретных процессов, в частности, функционирования станочных систем. Их особенность заключается в возможности отображения параллелизма, асинхронности и иерархичности.

На рис. 13.3 приводится сети Петри, где Р — конечное непустое множество позиций (состояний); Т — конечное непустое множество переходов (событий), причем 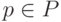и — функции входных и выходных инциденций; — начальная маркировка. Вершины сети 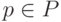изображены кружками, а вершины 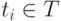— черточками (маркерами). Дуги соответствуют функциям инцидентности позиций и переходов. Точки в кружочках означают заданную начальную маркировку. Число маркеров в позиции равно значению функции 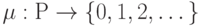. Переход от одной маркировки к другой осуществляется срабатыванием переходов. Переходt может сработать при маркировке 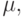если он является возбужденным:

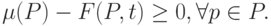
(13.10)

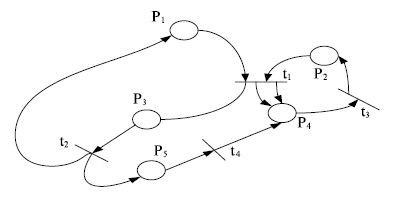
Рис. 13.3. Сеть Петри

Данное условие показывает, что в каждой входной позиции перехода t число маркеров не меньше веса дуги, соединяющей эту позицию с переходом. В результате срабатывания перехода t, удовлетворяющего условию (13.10), маркировку 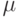заменяют маркировкой 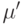по следующему правилу:

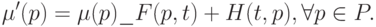
(13.11)

По этому правилу в результате срабатывания из всех входных позиций перехода t изымается F(p,t) маркеров и в каждую выходную позицию добавляется H(t,p) маркеров. Это означает, что маркировка 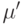непосредственно достижима из маркировки 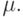Функционирование сети Петри — последовательная смена маркировок в результате срабатывания возбужденных переходов.

Состояние сети в данный момент времени определяется ее текущей маркировкой. Важная характеристика сети Петри — граф достижимости, с помощью которого описываются возможные варианты функционирования сети. Такой граф имеет вершины, которые являются возможными маркировками. Маркировк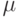и и 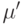соединяются в направлении t дугой, помеченной символами перехода 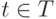или . Маркировка 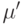такая последовательность переходов: является достижимой из маркировки 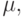если существует, что .

В качестве примера рассматривается сеть Петри, изображенная на рис. 13.3.

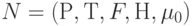, где Р = {Р₁, Р₂, Р₃, Р₄, Р₅},

. Функции F и Н заданы матрицами

P1

P2

P3

P4

P5

H =

t1

t2

t3

t4

t1

t2

t3

t4

F =

P1

P2

P3

P4

P5

Фрагмент графа достижимости для сети Петри приведен на рис. 13.4.

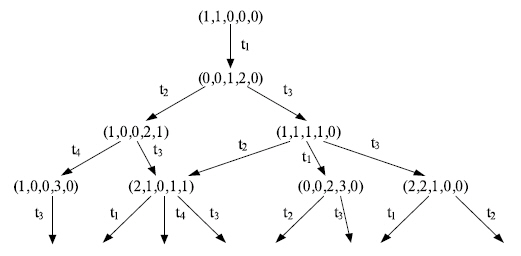
Рис. 13.4. Фрагмент графа достижимости сети Петри

Дата добавления: 2014-01-06