
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Обработка прямых многократных равноточных измерений
|
|
|
|
Теоретические положения
Обработка результатов измерений методом математической статистики
Под измерением понимается нахождение численного значения физической величины в установленных единицах с помощью средств измерений. Физическая величина – свойство, общее в качественном отношении многим физическим объектам, но в количественном отношении индивидуальное для каждого объекта.
Единство измерений – состояние измерений, при котором их результаты выражены в узаконенных единицах величин и погрешности измерений не выходят за установленные границы с заданной вероятностью.
В соответствии с этим положением результат измерения М должен представляться в виде трех чисел:
М = (Xд ± ε) P,
где Xд – действительное значение измеренной величины полученное определенным средством измерения;
ε – погрешность измерения, (доверительный интервал);
P – вероятность, с которой истинное значение X ист результата измерения находится в диапазоне доверительного интервала.
Например, запись (25±0.1)мм, 0.9 означает, что истинное X ист значение измеряемой величины находится в пределах 24.9 до 25.1 мм с вероятностью 90%.
При вероятности P равной 100% ее в результатах измерений не указывается.
Под истинным значением физической величины понимается значение, которое идеальным образом отражало бы качественную и количественную характеристику объекта. Исходя из этого, сформулированы основные постулаты метрологии:
- истинное значение измеряемой величины существует и оно постоянно;
- истинное значение отыскать невозможно, но оно связано с измеряемой величиной вероятностной зависимостью.
В зависимости от физической природы возникновения погрешности разделяются на систематические и случайные (см. пункт 4.15 с.51).
Методы обработки результатов измерений регламентированы ГОСТ 8.207-76.
Равноточность измерений сводится к тому, что измерения одного и того же параметра выполняется с одинаковой тщательностью при неизменных условиях. При этом необходимо, чтобы систематическая составляющая общей погрешности была устранена или имела меньший порядок малости. Порядок обработки результатов следующий:
6. Проводят измерение одного и того же параметра средством измерения подлежащим аттестации. Число измерений n должно быть больше 50. Результаты записывают в таблицу.
7. Исключают из результатов измерений грубые погрешности (промахи). При этом целесообразно использовать критерии Смирнова, Диксона и др. (1).
8. Определяют наибольшее Xmax, наименьшее Xmin опытное значение, размах варьирования R = Xmax, – Xmin.
9. Разбивают размах варьирования на равные 6-9 интервалов так, чтобы цена деления интервала с= R/r была больше цены деления по шкале прибора. (r – количество интервалов).
10. Определяют количество случайных величин mj (частота), значение которых находятся в определенном интервале и частность как отношение m/n. Результаты записывают в таблицу.
| Интервал (свыше…до) | Частота mj | Частость m I =n/mj | Теоретическая частота m tj | Критерий
 =(mj - m tj)2/ m tj =(mj - m tj)2/ m tj
|
6. Рассчитывают среднее арифметическое 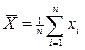 и среднее квадратичное S = +
и среднее квадратичное S = +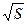 2 (
2 (
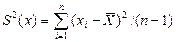 ). Для наглядности в координатах X- mj строят полигон рассеяния опытных величин.
). Для наглядности в координатах X- mj строят полигон рассеяния опытных величин.
7. Принимая σ = S и 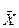 = M(x) по уравнению
= M(x) по уравнению
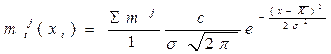 ,
,
определяют теоретическую частоту m tj ( где с – цена деления интервала). Для наглядности может быть построена теоретическая кривая нормального распределения в тех же самых координатах.
9. Для каждого интервала определяют значение параметра
 =(mj - m tj)2/ m tj
=(mj - m tj)2/ m tj
9. Сопоставляя суммарное значение  для определенного уровня значимости и числа степеней свободы с табличным значением делается вывод о справедливости принятой гипотезы нормального рассеяния.
для определенного уровня значимости и числа степеней свободы с табличным значением делается вывод о справедливости принятой гипотезы нормального рассеяния.
10. При подтверждении гипотезы нормального распределения для определенного значения вероятности определяют доверительный интервал:
ε = ±t (k)  S /
S / 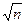 ,
,
где t – коэффициент Стьюдента.
Если гипотезу о нормальном распределении отвергают, то проводят проверку симметричности распределения по критерию Вилкоксона и ведут расчет с использованием медиан (1). Обработка результатов неравноточных измерений приведена в (1). Проверку гипотезы о нормальном распределении при малом числе измерений (менее 15) можно провести по методике, описанной в (1).
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 577; Нарушение авторских прав?; Мы поможем в написании вашей работы!