Деревья и графы

Эти структуры состоят из узлов и дуг (ветви):

1. Направленный граф:

type

PNTR=^TNode

TNode=record

DATA_ENTRIES:тип;

NPTR:array[1..N] of PNTR {массив указателей}

end;

Если N=1, получим однонаправленный список.

2. Ненаправленный граф:

type

PNTR=^TNode

TNode=record

DATA_ENTRIES:тип;

FORWARD:array[1..N] of PNTR {массив указателей вперёд}

BACKWARD:array[1..N] ofPNTR {массив указателей назад}

end;

Если N=1, получим двунаправленный список.

Дерево - частный случай графа, для которого установлено несколько ограничений:

1) обязательно должен присутствовать один узел, в который не входит ни одной ветви. Он наз. узлом Root или корневым узлом;

2) в любой другой узел входит не более одной ветви;

3) при описанных ограничениях в любой узел можно попасть из корневого узла за n шагов.

Древовидные структуры нужны в 2-х случаях:

1) нужно упорядочить некоторую информацию, представив её в виде иерархической структуры (система подкаталогов), в базах данных;

2) когда нужно обеспечить быстрый доступ к информации (применение двоичных деревьев).

Далее ограничимся рассмотрением бинарных деревьев.

Базовые операции: Add - добавить узел в дерево, Delete - удалить узел, Search - искать узел.

Для невырожденного (в список) бинарного дерева время поиска пропорционально log ₂ n, n - общее число узлов.

Пример двоичного дерева:

Правила построения дерева: Структура данных --->

Будем считать, что ключ-целое число без знака. Ключ узла определяет расположение узла в дереве. Генерироваться он может автоматически.

Правила добавления узлов:

При поступлении очередной записи на вход программы, поддерживающей дерево, ключ сравнивается последовательно со всеми ключами в дереве, начиная с корня, по принципу больше-меньше. Сравнивая с очередным узлом, направление перемещения к следующему узлу определяется из условия сравнения ключа добавляемой записи с узлом текущего узла по принципу больше-меньше.

Например: на вход программы поступают записи с ключами: 70,60,80,87,84. Как будет расти дерево (пустое).

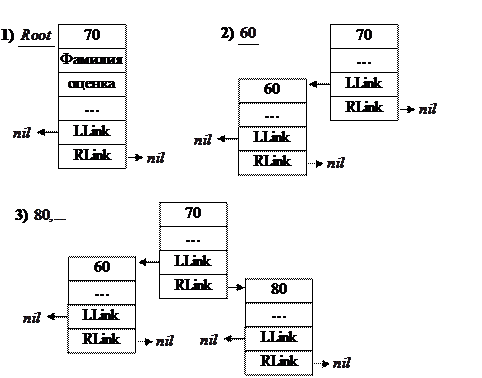При построении подобных структур, происходит автоматическое упорядочивание (сортировка) данных при добавлении.

Реализация операций над деревом:

Описание дерева:

type

NameStr=string[15];

Link=^Node

Node=record

Key:integer;

Name:NameStr;

Mark:integer;

…

LLink, RLink: Link

end;

var Root: Link;

Операция поиска:

Function FindTree(k:integer; var Prev:Link): Link;

{поиск нужной записи по ключу}

{Prev - вспомогательный параметр, через который передаётся указатель на узел, предшествующий найденному}

{Сама ф-ция FindTree возвращает указатель на найденный узел.}

var Curr: Link;

begin

Curr:=Root;

Prev:=nil;

While Curr<>nil do

if k=Curr^.Key they {нашли запись}

Begin FindTree:=Curr; Exit end

else

begin {продолжаем поиск}

Prev:=Curr;

{запоминаем указатель на предшествующую запись}

if k<Curr^.Key then Curr:=Curr^.LLink {делаем шаг влево}

else Curr:=Curr^.RLink {делаем шаг вправо}

end; {endif, enddo}

FindTree:=nil; {узел не найден}

end;

Включение новой записи:

(Прежде чем добавить новый узел, нужно найти, куда его можно добавить при помощи процедуры FindTree)

Procedure AddTree(A: Link); {А- указатель на добавляемый узел}

var P: Link;

begin {ищем узел, к которому можно добавить новый узел}

if FindTree (A^.Key, P)=nil then {А^.Key-ключ добавляемой записи}

{условие пустоты дерева}

if Root=nil then Root:=A {создаём корень}

else {дерево уже есть}

if A^.Key<P^.Key then P^.LLink:=A

{присоединили к левой ветви найденного узла}

else P^.RLink:=A

{присоединили к правой ветви найденного узла}

end;

Использование:

Var Node:Link;

…

New(Node);

Node^.Key:=уникальный ключ;

Node^.Name:=’Иванов’;

…

Node^.LLink:=nil;

Node^.RLink:=nil;

AddTree(Node);

…

Процедура распечатки значений, хранящихся в узлах дерева (в порядке возрастания ключей):

Procedure ListTree(p:Link); {P-указатель на корень}

begin

if p<>nil then

begin

ListTree(P^.LLink);

Writeln(P^.Key, P^.Name,…);

ListTree(P^.RLink)

end

end;

ListTree (Root); {Это рекурсивная процедуру}

{ Root - указатель на корень}

Рассмотрим пошаговую реализацию ListTree (Root):

1-ый вход в процедуру ListTree:

if p<>nil {условие истинно, т.к. p->100}

ListTree (P^.LLink)

------------------------------------------------------------------------------------------

2-й вход:

if p<>nil {p->20}

ListTree (P^.LLink)

------------------------------------------------------------------------------------------

3-й вход:

if p<>nil {p->15}

ListTree (P^.LLink)

------------------------------------------------------------------------------------------

4-й вход:

if p<>nil {условие ложно, p=nil}

{выход из процедуры на 3-й уровень}

------------------------------------------------------------------------------------------

3 (находимся на 3-м уровне вложенности вызова)

Writeln (P^.Key,…) {напечатали “15”,…}

ListTree(P^.RLink)

------------------------------------------------------------------------------------------

4-й вход:

if p<>nil {p=nil}

{выход на 3-й уровень}

------------------------------------------------------------------------------------------3 {здесь уже всё выполнили, выход на 2-й уровень}

------------------------------------------------------------------------------------------2 Writeln(P^.Key,…) {напечатали “20”,…}

ListTree(P^.RLink)

------------------------------------------------------------------------------------------

…

В конечном счёте будем иметь напечатанный узел с ключом 130 и выйдем из процедуры.

Каждый рекурсивный вызов как бы порождает новый экземпляр процедуры, все локальные переменные сохраняются.

Удаление узла (записи) из дерева:

Удаление узла из дерева реализуется просто, если из удаляемого узла выходит не более одной ветви.

Действия сводятся к перенаправлению указателей.

Если из узла выходят 2 ветви, появляется сложность сохранения целостности дерева. Чтобы решить эту проблему, необходимо для удаляемого узла найти узел замену.

Если из удаляемого узла выходят 2 ветви, решение проблемы поиска узла замены:

В двоичном дереве он всегда существует. Это либо самый правый узел левого поддерева, растущего из удаляемого узла, либо самый левый узел правого поддерева, растущего из удаляемого узла. Чтобы найти самый правый узел левого поддерева, нужно выйти из удаляемого узла по левой ветви и двигаться вправо (для второго варианта - наоборот).

Процедура удаления должна обрабатывать 3 ситуации:

1. Из удаляемого узла выходит не более 1-й ветви
2. Из удаляемого узла выходит 2 ветви
3. Удаляемый узел не найден.

Процедура рекурсивная и включает в свой состав ещё одну рекурсивную процедуру, вызываемую во 2-м случае (когда из узла выходит 2 ветви).

procedure DelTree (Var Curr:Link; k:integer);

{Curr:Link изначально указывает на корень дерева, k-ключ}

{Пример вызова: DelTree (Root,50);}

Var P:Link;

procedure Del (Var R:Link); {это локальная рекурсивная процедура}

Begin

if R^.RLink=nil then

Begin

P^.Key:=R^.Key; P^.Name:=R^.Name; …

P:=R; {сохранить указатель на удаляемый узел}

R:=R^.LLink; {удаление узла}

Dispose(P) {физическое удаление узла}

end;

else

Del(R^.RLink)

end;

{При возврате происходит присваивание R^.RLink:=R, R^.RLink – фактический параметр, R – формальный параметр. Логическое удаление происходит в момент выхода из процедуры Del}

Begin {начало процедуры DelTree}

if Curr=nil then {3-й случай, т.е. такой узел не найден}

Writeln(‘Узел не найден’)

else {продолжаем поиск}

if k<Curr^.Key then DelTree(Curr^.LLink,k) {двигаемся налево}

else

if k>Curr^.Key then DelTree(Curr^.RLink) {двигаемся направо}

else

Begin {узел найден, на него указывает Curr}

P:=Curr; {сохраняем указатель для удаления}

if P^.RLink=nil then

Begin

Curr:=P^.LLink; Dispose(P)

end

else

if P^.LLink=nil then

Begin

Curr:=P^.RLink; Dispose(P)

end

else

Del(P^.LLink) {2-й случай}

end

end;

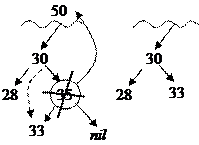Рассмотрим удаление узла дерева с ключом 50. (35 – узел, которым можно заменить удаляемый узел 50).

После удаления нижняя часть дерева будет иметь такой вид:

1-ый вход:

if Curr=nil

{условие ложно, т.к. Curr->100}

if k<Curr^.Key {да, k<100}

DelTree(Curr^.LLink,k)

{Curr^.LLink->20}

------------------------------------------------------------------------------------------

2-й вход:

if Curr=nil {Curr->20}

if k<Curr^.Key {нет, Curr^.Key=20}

if k>Curr^.Key {да, т.к. 50>20}

DelTree(Curr^.RLink,k)

------------------------------------------------------------------------------------------

3-й вход:

if Curr=nil {Curr->50}

if k<Curr^.Key {нет}

if k>Curr^.Key {да}

P:=Curr {нашли узел 50}

if P^.RLink=nil {нет}

if P^.LLink=nil {нет}

Del(P^.LLink) {2-й случай}

------------------------------------------------------------------------------------------

3 DelTree

1-й вход в Del:

if R^.RLink=nil {R->30; R^.RLink->35}

Del(R^.RLink)

------------------------------------------------------------------------------------------2-й вход в Del:

if R^.RLink=nil

{да, т.к. нашли узел, который можно перенести на место удаляемого (самый правый узел левого поддерева – с ключом 50)}

{переносим узел}

P^.Key:=R^.Key; P^.Name:=R^.Name; …

P:=R; {сохраняем указатель}

R:=R^.LLink; {удалили узел 35}

Dispoce(P); {физическое удаление}

{Выход из Del}

3. 1. (уровень вложенности)

Можно считать, что при выходе из Del произошло следующее присваивание: R^.RLink:=R. Реально такого присваивания не происходит, т.к. параметр передаётся в процедуру Del по адресу (как Var-параметр). В момент выхода из Del происходит логическое удаление узла.

Выход из Del.

3. (на третьем уровне) Выход из DelTree.

2. (на втором уровне) Выход из DelTree.

1. (на первом уровне) Выход из DelTree в основную программу.

{конец}

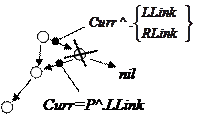В данном примере не рассматривалась ситуация удаления узла, из которого выходит не более одной ветви. Действия при этом аналогичны описанным. Удаление происходит опять в момент выхода из DelTree в результате выполнения следующего неявного оператора присваивания: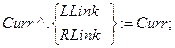

Графическая интерпретация --->

Примечание: Использовать рекурсивные процедуры необходимо с осторожностью. Причины: 1) текст программы плохо читаем, рекурсивные процедуры сложны для понимания; 2) использование рекурсивных процедур приводит к повышенным накладным расходам, т.е. расходы места в памяти на хранение внутренних переменных рекурс-й процедуры и потери времени на сохранение/восстановление этих переменных. Следствием сохранения локальных переменных рекурс-й процедуры в стеке является ограниченная глубина рекурсии. Это может вызвать проблему при обработке больших объёмов данных.

Дата добавления: 2014-01-07