Основное уравнение теплопередачи и уравнение теплового баланса

Теплопередача. Теплоотдача

Теплота от одной среды к другой может передаваться при непосредственном контакте или через стенку.

Если теплота переходит от более нагретой среды к менее нагретой через разделяющуюстенку, то процесс называется теплопередачей.

Если теплота переносится от стенки к среде (или наоборот), то процесс называется теплоотдачей.

В химической технологии теплообменные процессы осуществляются в аппаратуре, которая называется теплообменной аппаратурой.

Жидкости или газы, участвующие в теплообмене, называются рабочими средами.

Основной характеристикой теплообменного аппарата является поверхность теплообмена.

Связь между количеством теплоты передаваемым в аппарате и поверхностью теплообмена определяется основным кинетическим соотношением, которое называется о сновным уравнением теплопередачи:

(1)

- количество переданного тепла, Дж;

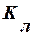- локальный коэффициент теплопередачи между средами, ;

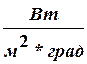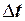- разность температур между средами,⁰С;

- элемент поверхности теплообмена, м² ;

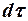- время теплообмена, с

- коэффициент теплопередачи средний для всей поверхности, .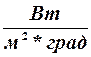

Физический смысл коэффициента теплопередачи:

Коэффициент теплопередачи показывает, какое количество теплоты в Дж переходит в 1с от более нагретого тела к менее нагретому через поверхность теплообмена в 1м² при средней разности температур равной 1 град. Коэффициент теплопередачи определяет интенсивность теплообмена. Из основного уравнения теплопередачи (1) можно определить поверхность теплопередачи . . (2)

определяется из уравнения теплового баланса:

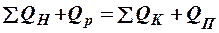(3)

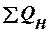- потоки тепла, которые поступают в аппарат с исходными продуктами;

- теплота реакций (теплота химических превращений; испарение жидкостей; выделение паров или газов из твердых поглотителей; теплота плавления и растворения). Для определения этих теплот используют справочные данные.

- потоки тепла, которые выходят из аппарата с конечными продуктами;

- потери тепла в окружающую среду (» 3¸5%).

Теплопроводность

Закон Фурье ( установлен опытным путем) – количество теплоты переданного теплопроводностью, прямо пропорционально градиенту температуры 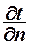, времени 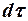и площади сечения 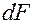, перпендикулярного направлению теплового потока:

, (4)

- коэффициент теплопроводности, Вт/м∙град.

Коэффициент теплопроводности l показывает, какое количество теплоты в Дж проходит в 1с через 1м² поверхности при разности температур в 1⁰ на единицу длины нормали к изотермической поверхности. (Изотермическая поверхность - геометрическое место точек с одинаковой температурой).

Плотность теплового потока 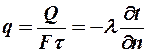. (5)

(²-² означает что тепло перемещается в сторону падения температуры).

Дифференциальное уравнение теплопроводности

Процесс распространения теплоты теплопроводностью математически описывается дифференциальным уравнением, выведенным на основе закона сохранения энергии.

; (6) –

Дифференциальное уравнение теплопроводности в неподвижной среде. 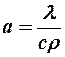- коэффициент температуропроводности; характеризует теплоинерционные свойства вещества. Чем больше , тем тело быстрее охлаждается (нагревается).

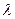,, - не изменяются по направлению и во времени.

Для стационарных процессов -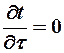, т.е. температура не меняется со временем и уравнение (6) принимает вид . Т.к. а¹0, то (7)

или 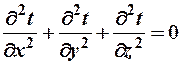- Дифференциальное уравнение теплопроводности в неподвижной среде при стационарном тепловом режиме. Уравнения (6) и (7) дают возможность решать задачи связанные с распространением тепла в теле путем теплопроводности как при стационарном, так и при нестационарном тепловом режиме. При решении конкретных задач уравнения дополняются соответствующими начальными и граничными условиями.

Теплопроводность плоской стенки

В инженерной практике часто встречаются задачи стационарной теплопроводности через плоскую и цилиндрическую стенки. Это задачи расчета тепловой изоляции аппаратов и трубопроводов.

Стенка состоит из однородного материала; d - толщина стенки; l - теплопроводность материала стенки; t_ст1, t_ст2 – температура стенки. t_ст1 > t_ст2.

Вывод уравнения теплопроводности плоской стенки

Запишем уравнение Фурье в развернутом виде

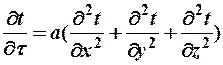
При стационарном режиме температура в различных точках постоянна во времени, т.е

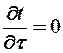
Температурное поле одномерно (плоская стенка) .

Т.о. уравнение Фурье приобретает вид: d²t/dx²=0.

Проинтегрируем дважды: dt/dx = C₁; t = C₁x+C₂. C₁ и С₂ найдем из условий на границе: х=0; х=d. При х=0 t_ст1=С₂, а при х=d t_ст2= C₁d+ t_ст1;

C₁=(t_ст2- t_ст1)/d; В результате получим

t=x(t_ст2- t_ст1)/d+ t_ст1 (8)

Температура по толщине стенки х меняется линейно, температурный градиент сохраняет постоянное значение. Подставим полученное значение градиента температуры в (4)-з. Фурье и получим уравнение теплопроводности плоской стенки при стационарном тепловом режиме

dQ=l/d(t_ст1 - t_ст2)dFdt.

Q=l/d(t_{ст 1} - t_ст2)Ft (9).

Здесь l/d - термическая проводимость стенки.

Теплопроводность цилиндрической стенки (самост.)

В тепловых процессах одновременно с теплопроводностью и конвекцией почти всегда имеет место тепловое излучение, причем, чем выше температура тела, тем больше тепла оно передает в виде теплового излучения.

Тепловое излучение

- это процесс распространения энергии в форме электромагнитных волн.

Дата добавления: 2014-01-07