Понятие о динамической расчетной схеме

Под понятием расчетной динамической схемой понимается схема расположения совокупности инертных элементов системы, при расчетах на динамические воздействия.

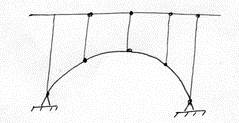
Динамическая расчетная схема классифицируется в зависимости от числа степеней свободы, которое определяется положением инертных элементов в плоскости или пространстве в любой момент времени.

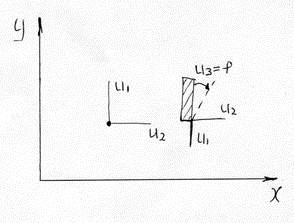
Сосредоточенная масса имеет в плоскости 2 степени свободы, а в пространстве 3 степени свободы.

Тело определенных размеров в плоскости имеет 3 степени свободы, а в пространстве 6.

По числу степени свободы расчетная схема динамического сооружения классифицируется на:

1. Системы с 1 степенью свободы

2. Системы с конечным числом степени свободы

3. Системы с бесконечным числом степени свободы

Пример:

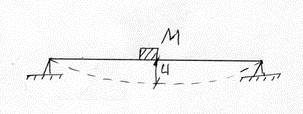
1 степень свободы

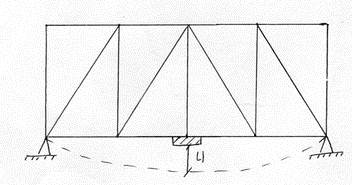
2 степени свободы.

Для моделирования систем с одной степенью свободы применяется универсальная модель в виде груза на пружине

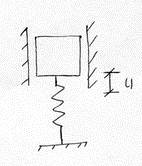с 1 степенью свободы.

Для оценки жесткости и податливости упругой связи поддерживающий инертный элемент применяется 2 понятия:

1. Коэффициент податливости ()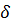

2. Коэффициент жесткости (с)

с – коэффициент жесткости упругой связи – это величина силы или пары сил которую необходимо приложить к инертному элементу, чтобы вызвать его единичное перемещение линейное или угловое.(Н/м; Н*м/рад)

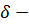коэффициент податливости – это величина перемещения линейного или углового которое возникает при приложении к инертному элементу единичной силы или пары сил. (м/Н; рад/Н*м)

Коэффициент податливости определяется из формулы Мора:

(4) – изгибаемые конструкции.

m – эпюра моментов от единичного воздействия по направлению податливости искомой связи.

Конечное число степеней свободы.

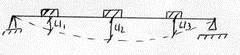
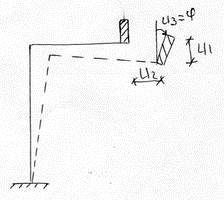
(i=1,2,3….n)

Дата добавления: 2014-01-06