И потенциалом

Связь между напряженностью электрического поля

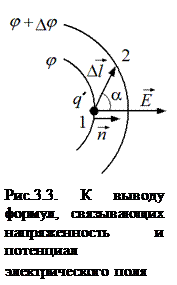
Напряженность электрического поля и потенциал связаны между собой. Установим эту связь. Для этого, рис.3.3, проведем две близкорасположенные эквипотенциальные поверхност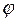и и . Как было показано выше, вектор 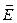перпендикулярен эквипотенциальной поверхности. Работа по перемещению пробного заряда q’ из точки 1 с потенциалом 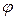в точку 2 с потенциалом 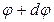согласно формуле (10) равна 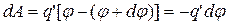. С другой стороны

,

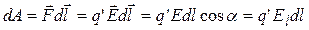где E_l – проекция вектора 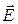на направление перемещения .

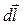Таким образом 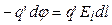, отсюда

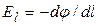. (3.11)

Величина 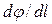- характеризует быстроту изменения потенциала в направлении .

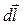Производные (3.11) можно брать в направлении координатных осей, тогда

.

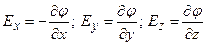Через проекции вектора 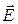, можно выразить сам вектор:

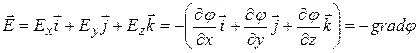. (3.12)

В последнем выражении векторная функция 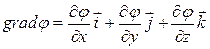называется градиентом скалярного поля j. Последнее выражение можно также записать с использованием оператора Ñ (произносится «оператор набла»):

;

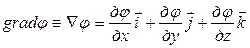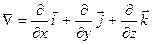
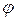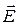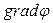Градиент потенциала j есть вектор, направленный по нормали к эквипотенциальной поверхности в сторону наибыстрейшего возрастания . Знак "минус" в (3.12) означает, что и направлены в противоположные стороны.

Пример 1. Применим формулу (13) для нахождения напряженности поля точечного заряда по известной формуле для потенциала

.

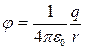Модуль вектора напряженности:

.

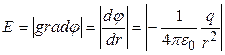Направление вектора 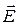зададим с помощью радиус-вектора 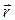, проведенного от заряда в данную точку поля:

.

Далее решим обратную задачу нахождения разности потенциалов Dj поля по известному распределению вектора напряженности. Пусть заряд q’ перемещается из точки 1 в точку 2, как показано на рис.3.3. Работа по его перемещению силами поля может быть выражена двояко:

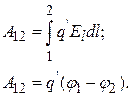
Объединяя эти выражения, получим:

.

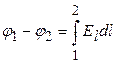Пример 2. Найдем связь между напряженностью и потенциалом в случае однородного поля, рис.3.4. Работа по перемещению заряда из точки 1 в точку 2 по произвольной криволинейной траектории равна

.

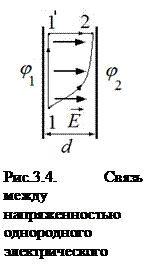
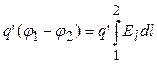Заменим эту траекторию ступенчатой траекторией 1-1’-2, тогда Но в потен

.

Здесь первый интеграл равен нулю, поскольку в любой точке этой части траектории вектор напряженности перпендикулярен перемещению. Таким образом, получено:

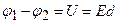. (3.13)

Дата добавления: 2014-01-07