Поступательное движение

Кинематика материально точки

Механикой называется раздел физики, изучающий движение тел. В том случае, когда нас не интересует движение отдельных частей тела, мы будем пользоваться моделью материальной точки. Материальная точка – точка, обладающая массой исследуемого тела. Следует отметить, что в отличии от тела конечной массы и геометрических размеров на материальную точку не действуют силы инерции. Траекторией движения тела называют линию, которую описывает тело при своем движении. Для того, чтобы начать наблюдать за движущимся телом необходимо сначала ввести систему координат.

На практике, часто бывает удобно вводить декартову прямоугольную правовинтовую систему координат (см. приложение). Радиус вектор из начала координат определяет координаты (x,y,z) тела. Основной задачей механики, называют задачу нахождения координат тела в любой момент времени. Если мы смогли найти закон изменения радиус-вектора от времени , то мы решили основную задачу механики.

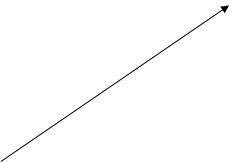
Пусть тело (материальная точка) движется на плоскости по некоторой траектории, изображенной на рис. 1. Для описания такого движения достаточно ввести две координаты x и y. Начало координат выбираем произвольно, как нам будет удобно описывать движение. Если тело, движется вдоль прямой линии, то удобно ввести одну координатную ось и начало координат поставить там, где мы за телом начали наблюдать. В выборе системы координат мы не ограничены.

y 1

2

O x

Рис. 1. Пример плоского поступательного движения

В точке наблюдения 1 материальная точка имеет координаты , а в точке 2 –. Разницу векторов между двумя точками наблюдения 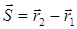называют вектором перемещения. Длину траектории между точками 1 и 2 путем или расстоянием, пройденным телом от точки 1 до точки 2.

Скорость материальной точки определяется как первая производная радиус-вектора по времени или предел малого перемещения Δ S к малому интервалу времени Δ t:

.

(1)

Направление вектора скорости, исходя их геометрического смысла производной – касательная к точке траектории, в которой считается скорость.

Если в результате исследования, скорость остается постоянной , то такое движение называют равномерным. При равномерном движении, тело проходит равные расстояния за одинаковые промежутки времени. Если в процессе наблюдения за движением материальной точки скорость изменяется со временем, то необходимо находить производные следующих порядков по времени.

Скорость изменения скорости, или вторую производную от радиуса-вектора, называют ускорением:

.

(2)

Если ускорение в процессе движения тела остается постоянным, то такое движение называют равноускоренным. В равноускоренном движении разделяют два вида: равноускоренное () и равнозамедленное (). При равноускоренном движении скорость тела увеличивается или уменьшается на одинаковые значения за равные промежутки времени.

Дата добавления: 2014-01-07