Динамика вращательного движения тела

При вращательном движении тела конечной геометрии применение ранее полученных величин не удобно, поскольку линейные скорости точек тела и их ускорения зависят от радиуса поворота. Поэтому удобнее получить законы в угловых скоростях и ускорениях, которые не зависят от радиуса поворота. Угловые величины всех точек тела одинаковы и не зависят от расстояния до оси вращения.

Рассмотрим вращающиеся тело произвольной геометрии, изображенное на рис. 4.

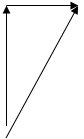
Будем мысленно наблюдать за точкой вращающегося тела. Радиус-вектор 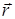разложим на две составляющие 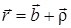, где вектор 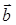– лежит на оси вращения z, а вектор 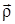– радиус поворота точки. В общем виде, вектор момента импульса 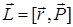ориентирован под углом 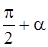к оси вращения z, где α – угол наклона радиус-вектора к оси вращения z, и этот угол зависит от выбора начала координат расстояния от оси вращения до рассматриваемой точки. Поэтому удобнее определить проекцию момента импульса на ось вращения .

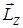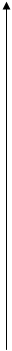z a z^’

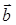
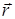
О O ^’ y

x

Рис. 4. Пояснение к выводу уравнений динамики вращательного движения

Рассчитаем проекцию вектора момента импульса на ось вращения:

,

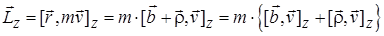т.к. вектор 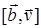перпендикулярен оси вращения, его проекция на ось z: 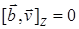, далее подстановкой в 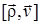формулы (6) имеем:

,

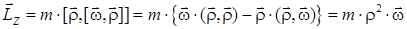вектора 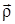и 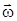– взаимно перпендикулярны, поэтому 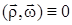. Получено важное выражение, в котором проекция момента импульса на ось вращения точки зависит от произведения ее массы на квадрат расстояния от оси вращения. Для тела конечной геометрии, сумма всех масс элементарных точек на квадрат расстояния от оси вращения будет величиной конечной. Эта величина называется моментом инерции тела:

,

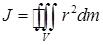(19)

здесь интеграл берется по всему объему тела. Момент инерции называют механическим моментом второго порядка. Моменты инерции простейших тел приведены в справочных таблицах.

Если момент инерции тела J относительно оси OZ известен, то момент инерции тела J’ относительно параллельной оси O’Z’ вычисляется по теореме Штерна:

,

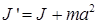(20)

где a – расстояние между осями OZ и O’Z’.

Исходя из вышеизложенного, можно написать три уравнения динамики вращательного движения тела:

.

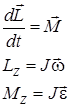(21)

Дата добавления: 2014-01-07