
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Основы специальной теории относительности. В ньютоновской механике, при переходе от одной системы координат O(x, y, z, t) к другой O’(x’, y’, z’
|
|
|
|
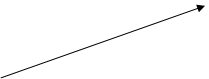
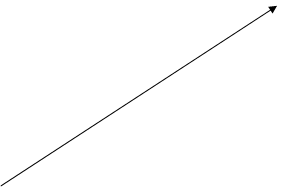
В ньютоновской механике, при переходе от одной системы координат O (x, y, z, t) к другой O’ (x’, y’, z’, t’), изображенных на рис.7, движущейся относительно O поступательно с постоянной скоростью  , пользуются преобразованиями координат и времени, которые называют преобразованиями Галилея:
, пользуются преобразованиями координат и времени, которые называют преобразованиями Галилея:
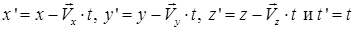 , ,
|
или
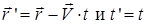 , ,
|
где 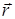 и
и 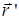 – координаты точки в момент времени t = t ’ в системе координат O и O’.
– координаты точки в момент времени t = t ’ в системе координат O и O’.
Из преобразований координат следует преобразование скоростей в одной системе, относительно другой:
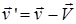 , ,
|
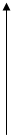 Далее, вычисляя ускорения в разных системах координат из преобразований Галилея, получим, что
Далее, вычисляя ускорения в разных системах координат из преобразований Галилея, получим, что 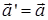 , и силы, действующие в разных системах координат, то же равны.
, и силы, действующие в разных системах координат, то же равны.
z’
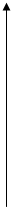 |
 z
z
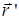
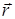

 O’
O’
y’
x’ 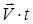
O
 y
y
x
Рис. 7. Пояснения к выводу преобразований Галилея и Лоренца
Таким образом, в ньютоновской механике справедлив механический принцип относительности: законы механики одинаковы во всех инерциальных системах координат. Следовательно, с помощью любых механических экспериментов, проведенных в замкнутой системе тел, не возможно установить покоится эта система тел или движется.
Во-первых, механический принцип относительности Галилея не дает ответа о равноправности замкнутых систем отсчета при движении одной системы относительно другой с любой скоростью, а также о их равноправности для других, не механических, явлений. Во-вторых, как известно скорость механического движения не может быть любой. Предельная скорость движения ограничена скоростью распространения электромагнитных волн в вакууме (скоростью света в вакууме 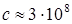 м/с). Поэтому была разработана универсальная теория относительности измерений координат и времени в движущейся инерциальных системах отсчета, в которой скорость любого механического движения не может превышать скорости света в вакууме. В специальной теории относительности, как и в ньютоновской механике, предполагается однородность времени и однородность и изотропность пространства.
м/с). Поэтому была разработана универсальная теория относительности измерений координат и времени в движущейся инерциальных системах отсчета, в которой скорость любого механического движения не может превышать скорости света в вакууме. В специальной теории относительности, как и в ньютоновской механике, предполагается однородность времени и однородность и изотропность пространства.
В основы специальной теории относительности положено два постулата:
1) в любых инерциальных системах отсчета все физические явления при одних и тех же условиях протекают одинаково;
2) скорость света в вакууме не зависит от движения источника света.
Постулаты теории относительности противоречат классической ньютоновской механике о свойствах пространства и времени, приведенных в преобразованиях Галилея.
Исходя из второго постулата теории относительности и ограниченности скорости движения скоростью света в вакууме можно получить преобразования координат и времени при измерении из покоящейся системы координат в движущуюся и наоборот. При этом единственным инструментом измерения при невозможности перемещения с линейкой и секундомером на другую систему координат, в виду ее удаленности или малости летящего объекта (пучок элементарных частиц), является световой импульс. Для этого достаточно рассмотреть одномерный случай, когда одна из осей, пусть ось x’, подвижной системы координат совпадает по направлению с скоростью  движения ее центра О’, относительно неподвижной системы координат. Выбор такого расположения осей координат является следствием первого постулата теории относительности при повороте осей декартовой системы координат.
движения ее центра О’, относительно неподвижной системы координат. Выбор такого расположения осей координат является следствием первого постулата теории относительности при повороте осей декартовой системы координат.
Преобразования выглядят следующим образом и называются преобразованиями Лоренца:
 . .
| (40) |
Здесь с – скорость света в вакууме; t, x, y, z и t’, x’, y’, z’ – время и координаты точки в системе координат xyz и в системе координат x'y'z’ соответственно, измеренные из системы координат O.
Преобразования Лоренца можно получить из постулатов теории относительности следующим образом. Мысленно из начала обеих координат запускаем световой импульс, распространяющийся в вакууме. В обеих системах координат, конец светового импульса опишет сферы радиусами c·t и c·t’ в системе координат O и O’ соответственно. Уравнения этих сфер в разных системах координат:
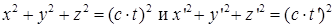 . .
|
После переноса всех слагаемых в левую часть
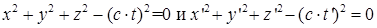
|
уравниваем тождественно левые части уравнений
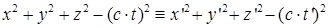 . .
| (41) |
Следует заметить, что с точки зрения теории чисел, простого равенства в (41) недостаточно, поскольку уравнивается нуль с нулем, а на множестве вещественных чисел ноль определяется как число, получаемое бесконечным делением любого целого числа на любое целое. Поэтому выражения уравнены тождественно, т.е. левая часть всегда равна правой.
Решение уравнения (41) будем искать в виде линейных комбинаций:
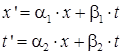 , ,
|
другие координаты равны между собой, в виду вышеописанного выбора ориентации систем координат xyz и x’y’z’, а именно: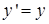 и
и  .
.
Координаты начала координат подвижной системы, точки O’ в системах координат xyz и x’y’z’: 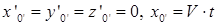 . Подставляя эти значения в линейные комбинации, получаем:
. Подставляя эти значения в линейные комбинации, получаем:
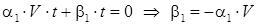 . .
|
Аналогично, координаты начала координат неподвижной системы, точки O в системах координат xyz и x’y’z’ равны: 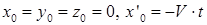 . Подставляя эти значения в линейные комбинации, получаем:
. Подставляя эти значения в линейные комбинации, получаем: 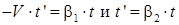 , т.е.
, т.е. 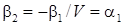 .
.
Таким образом, искомые линейные комбинации можно представить в виде:
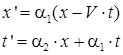 , ,
| (42) |
Подстановка полученных линейных комбинаций пространственного выбора систем координат (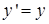 и
и  ) в тождество (41) дает:
) в тождество (41) дает:
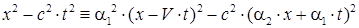 . .
| (43) |
Раскрываем скобки в тождестве (43), переносим все слагаемы в левую часть, и приводим подобные слагаемые при координате и времени::
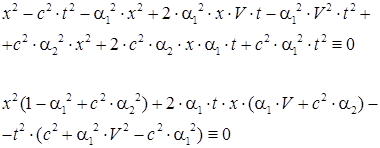 . .
|
Для выполнения условия тождественности равенства необходимо потребовать равенства нулю членов в скобках, поскольку они не зависят от переменных величин: координат и времени. Тогда, уравнивая нулю члены в скобках, получаем систему уравнений:
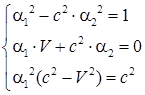 . .
|
Решение последнего уравнения системы дает коэффициент α1, а подстановка в первое уравнение – коэффициент α2.
Откуда получаем неизвестные коэффициенты искомой линейной комбинации (42)
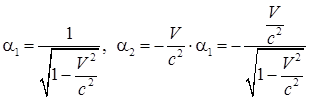 , ,
|
и их подстановка в нее же даст преобразования Лоренца (40).
Механика движения тел с большими скоростями порядка скорости света называется релятивисткой механикой. Как видно из преобразований Лоренца, при 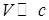 , они переходят в преобразования Галилея для классической ньютоновской механики.
, они переходят в преобразования Галилея для классической ньютоновской механики.
Из преобразований Лоренца вычислим преобразование скоростей в релятивисткой кинематике:
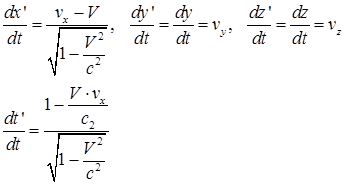 . .
|
Так как
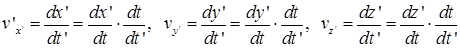 , ,
|
то связь между проекциями скоростей точек на оси в декартовых системах координат xyz и x’y’z’ имеет вид:
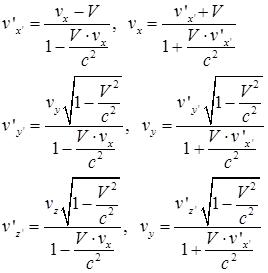 . .
| (44) |
Следствием из преобразования Лоренца является сокращение продольных (в направлении скорости движения системы координат) размеров тела, поперечные размеры остаются постоянными и сокращение интервала между двумя событиями в разных системах координат:
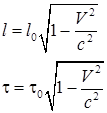 , ,
| (45) |
где l 0 и τ0 – длина отрезка и интервал между двумя событиями в неподвижной системе координат. Сокращение временного интервала между двумя событиями, не означает замедление хода часов в движущейся системе координат. Часы в обеих системах идут одинаково.
Из первого постулата теории относительности для выполнения основного закона классической механики Ньютона (15) и лоренцевского сокращения длины следует увеличение массы тела, измеренной в подвижной системе координат, относительно неподвижной:
 , ,
| (46) |
m 0 – называют массой покоя тела, при v =0.
Основное уравнение релятивисткой динамики имеет вид
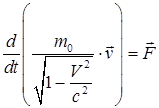 , ,
| (47) |
где
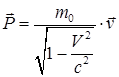
|
– релятивистский импульс тела. Соотношение между кинетической энергией и импульсом остается одинаковое в классической и релятивистской механике:
 . .
| (48) |
Полная энергия системы равна произведению релятивистской массы системы на квадрат скорости света в вакууме:
 . .
| (49) |
Глава 2. МОЛЕКУЛЯРНАЯ ФИЗИКА. ТЕРМОДИНАМИКА
Термодинамика газов – наука, изучающая изменение состояния газа при вариации температуры. Из свойства газов известно, что газ занимает весь предоставленный ему объем, за исключением тяжелых газов. Например, элегаз (фторид серы VI – SF6) можно переливать, как воду из стакана в стакан. Название этот газ получил ввиду его высоких изоляционных (диэлектрических) свойств, и используется как заполнитель в высоковольтных переключателях.
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 408; Нарушение авторских прав?; Мы поможем в написании вашей работы!