Законы Ньютона

Как и любая область человеческих знаний, классическая механика содержит в своей основе некоторое количество основных утверждений (законов), из которых логическим образом вытекают многочисленные следствия. Впервые основные законы динамики были сформулированы И.Ньютоном в 1687 г., как результат обобщения огромного общечеловеческого опыта. Несмотря на определенную ограниченность этих законов, они играют огромную и исключительную роль в механике. Основных законов динамики три.

Первый закон Ньютона - устанавливает условия, при которых механическое состояние материальной точки остается неизменным с течением времени.

Материальная точка (тело) сохраняет состояние покоя или равномерного прямолинейного движения, если она не взаимодействует с другими телами или ее взаимодействие с другими телами скомпенсировано.

Поскольку механическое движение относительно и его характер существенным образом определяется выбором системы отсчета, становится понятным, что первый закон Ньютона выполняется только в тех системах отсчета, которые движутся относительно друг друга равномерно и прямолинейно либо относительно друг друга покоятся. Такие системы отсчета называют инерциальными. Системы отсчета, в которых первый закон Ньютона не выполняется, называются неинерциальными. В дальнейшем будет показано, что во всех инерциальных системах отсчета ускорение материальной точки имеет одно и то же значение, а в различных неинерциальных системах ускорения одной и той же материальной точки различны.

Здесь следует четко понимать, что инерциальные системы отсчета являются в определенной степени идеализацией реальных систем отсчета. Реальную систему отсчета можно считать инерциальной с той точностью, с какой в ней выполняется первый закон Ньютона.

Из многочисленных опытных данных известно, что гелиоцентрическая система отсчета, то есть система отсчета, связанная с Солнцем, оси которой ориентированы в направлении определенных звезд, является инерциальной.

Многие задачи механики можно решать, считая инерциальной систему отсчета, связанную с Землей.

Второй закон Ньютона - устанавливает условия, при которых механическое состояние материальной точки изменяется.

Во втором законе содержится утверждение, что изменение механического состояния материальной точки может произойти только в результате взаимодействия этой точки с другими телами.

Введем физические величины, с помощью которых устанавливается математическая форма второго закона.

Как уже указывалось, в качестве количественной меры изменения механического состояния материальной точки принимается ее ускорение 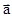, а количественной меры взаимодействия - сила .

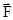Определим некоторые свойства механической силы.

1) Если на материальную точку поочередно действуют силы 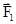и 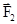, которые вызывают равные ускорения этой точки 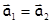, то силы 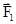и 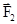называются равными, то есть =.

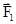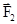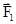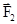2) Если на точку одновременно действуют две силы и , в результате чего точка приобретает ускорение 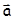, то всегда можно действие этих сил заменить действием одной силы 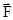, вызывающей точно такое же ускорение 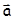этой точки. В этом случае сила 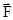называется равнодействующей сил 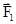и .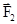

Утверждения 1) и 2) легко обобщаются на случай произвольного количества сил, действующих на одну материальную точку, и, по сути, устанавливают способы количественного сравнения механических сил.

Из опыта хорошо известно, что при действии одинаковых сил на разные материальные точки 1 и 2 изменения их механического состояния, вообще говоря, различны, то есть 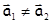. В этом проявляется различная “сопротивляемость” материальных точек по отношению к внешнему воздействию. Это “стремление” материальных точек сохранить свое механическое состояние называется инертностью. Физическая величина, характеризующая это свойство инертности, называется массой материальной точки.

На основании опыта устанавливаются следующие способы количественного сравнения масс различных материальных точек:

1) Если при действии одинаковых по величине сил 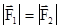на различные материальные точки 1 и 2 их ускорения оказываются равными 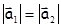, то принимается, что массы этих точек так же равны, то есть

m₁ = m₂;

2) Если при действии одинаковых сил 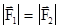, , 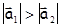то .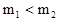

Рассмотрим теперь идеализированную физическую модель, когда механическая система состоит из двух взаимодействующих материальных точек 1 и 2. Окружающие их тела будем считать настолько удаленными, что воздействием на эти точки можно пренебречь по сравнению с взаимодействием этих точек между собой. Такая система материальных точек, не взаимодействующая с окружающими телами, называется замкнутой. В этом случае, многочисленные опытные данные свидетельствуют о том, что, независимо от природы взаимодействия между точками, всегда выполняется равенство

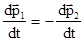. (2.3)

В равенстве (2.3) величина

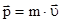(2.4)

называется импульсом материальной точки.

Другими словами, равенство (2.3) означает, что в замкнутой системе при взаимодействии двух материальных точек между собой скорости изменения их импульсов равны по величине и противоположны по направлению в каждый момент времени. Из (2.3) следует важное следствие:

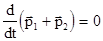
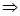
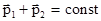, (2.5)

которое означает, что в замкнутой системе двух материальных точек их суммарный импульс остается постоянным. Это следствие является частным проявлением более общего закона сохранения импульса.

В случае, если в процессе взаимодействия массы материальных точек остаются постоянными, то равенству (2.3) с учетом (2.4) можно придать вид

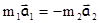. (2.6.)

Поскольку одним из результатов взаимодействия двух точек является скорость изменения импульса одной из них, то в качестве количественной меры механической силы, действующей на материальную точку, примем именно скорость изменения импульса этой материальной точки, то есть

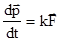. (2.7)

Здесь мы, конечно, отвлекаемся от того факта, что сила 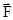есть результат действия другой материальной точки на данную.

Для m = const соотношению (2.7) можно придать вид

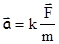. (2.8)

В соотношениях (2.7) и (2.8) 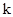- это коэффициент пропорциональности, зависящий от выбора системы единиц измерения физических величин. В системе СИ k = 1, единица силы Ньютон (Н): 1Н = 1 кг×м/с².

Соотношения (2.7) и (2.8) выражают в математической форме содержание второго закона Ньютона и отражают связь между причиной изменения движения 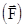, результатом этого изменения 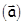и инертными свойствами материальной точки (m). Эти соотношения позволяют предсказать состояние материальной точки в момент времени t + dt, если известны ее состояние и сила, действующая на материальную точку в момент времени t. Действительно, из (2.7) следует, что

.

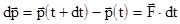
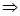
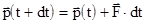Поэтому (2.7) и (2.8) являются математическими выражениями принципа причинности в классической механике и носят название “основное уравнение динамики материальной точки” (динамики поступательного движения твердого тела).

В классической механике большую роль играет так называемый принцип независимости действия сил, который имеет следующее содержание.

При действии на материальную точку нескольких сил одновременно каждая из этих сил независимо друг от друга сообщает материальной точке такое ускорение, которое было бы у точки в отсутствии других сил (рис. 2.1).

Поэтому, на основании второго закона Ньютона,

, ,

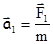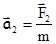так как

рис. 2.1

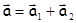, то

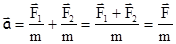, (2.9)

где 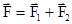-равнодействующая сил , .

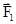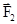Случай действия двух сил на частицу легко обобщается на любое количество сил. Использование этого принципа позволяет складывать силы, действующие на материальную точку, а также разлагать силу на составляющие по любым двум или более направлениям. При этом необходимо четко себе представлять, что сила количественно описывает взаимодействие двух тел (точек) между собой, составляющие же силы не соответствуют никакому взаимодействию, поэтому физического смысла не имеют.

Третий закон Ньютона - фактически устанавливает равноправие объектов, взаимодействующих между собой.

Силы взаимодействия между материальными точками 1 и 2 направлены вдоль прямой, соединяющей эти точки, равны по величине и противоположны по направлению (рис. 2.2).

То есть

    Рис. 2.2

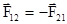, (2.10)

здесь 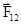- cила, действующая на первую точку со стороны второй, 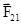- на вторую со стороны первой.

Следует обратить внимание, что равенство 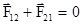совсем не означает, что равнодействующая этих сил равна нулю. Равнодействующей сил взаимодействия не существует, так как эти силы действуют на разные материальные точки.

В заключение обсуждения законов Ньютона отметим, что они являются не отдельными независимыми друг от друга законами, а представляют собой единый комплекс взаимосвязанных законов.

Вывод: Законы Ньютона являются опытными постулатами классической механики и устанавливают причины возникновения механического движения.

2.3. Силы

Как уже указывалось в 2.1, в механике различают два типа взаимодействий: полевые и контактные.

К полевым взаимодействиям относятся три вида фундаментальных взаимодействий, известных в современной физике: гравитационное, электромагнитное, сильное. В классической механике основную роль играют первые два вида взаимодействия, которые будут рассмотрены ниже.

2.3.1. Гравитационное взаимодействие

Гравитационное взаимодействие описывается опытным законом Ньютона - законом всемирного тяготения: две материальные точки с массой m₁ и m₂, находящиеся на расстоянии r друг от друга, притягиваются с силой

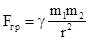, (2.11)

где g=6.67×10^-11 Н×м²/кг² - гравитационная постоянная. Масса m₁ и m₂

материальных точек, входящих в закон всемирного тяготения, называется гравитационной массой.

Современные опытные данные свидетельствуют о том, что инертная масса m, входящая во второй закон Ньютона, и гравитационная масса m, входящая в закон всемирного тяготения, равны между собой с относительной точностью 10^-12. Эти опытные данные положены в основу так называемого принципа эквивалентности гравитационных и неинерциальных сил, возникающих в неинерциальных системах отсчета.

Закон всемирного тяготения в форме (2.11) строго справедлив для неподвижных друг относительно друга материальных точек и приближенно при движении с относительной скоростью u_отн << с. Его можно применять в виде (2.11) для однородных правильной геометрической формы тел. В этом случае r означает расстояние между геометрическими центрами тел.

Для неоднородных тел любой формы (2.11) можно использовать, если известны положения центров масс этих тел, тогда r означает расстояние между центрами масс гравитационно взаимодействующих тел.

Рассмотрим некоторые частные случаи проявления гравитационного взаимодействия.

Сила тяжести - сила гравитационного притяжения, действующая на материальную точку (тело) со стороны некоторой планеты (например, Земли). В результате действия этой силы тело движется с ускорением. На основании второго закона Ньютона имеем

,

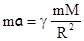где m - масса материальной точки, M - масса планеты, R - расстояние от центра планеты до материальной точки, или

.

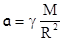Здесь учтено, что инертная и гравитационная массы равна в соответствии с принципом эквивалентности.

Этот результат означает, что ускорение, с которым материальная точка движется под действием силы гравитационного притяжения к планете, не зависит от массы m материальной точки, то есть для всех материальных точек одинаково, и называется ускорением свободного падения.

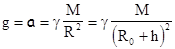, (2.12)

где R₀ - радиус планеты, h - высота материальной точки над поверхностью планеты.

Вблизи поверхности планеты (h << R₀)

.

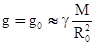Сила, вызывающая свободное падение материальной точки с ускорением g, называется силой тяжести:

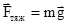. (2.13)

Вес тела - сила, с которой тело действует на связь (подвес, опору), удерживающую это тело от свободного падения.

На основе третьего закона Ньютона со стороны связи на тело действует сила реакции связи :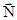

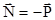. (2.14)

В результате действия двух сил 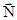и 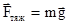в общем случае тело может двигаться с ускорением 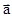, то есть

.

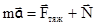С учетом (2.13) и (2.14) последнее равенство примет вид

,

откуда

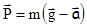. (2.15)

В случае 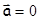(покоящееся или движущееся с постоянной 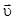скоростью тело)

.

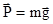В случае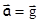

.

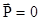Такое состояние называется невесомостью. Здесь следует подчеркнуть, что вес тела 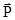и сила тяжести 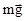действуют на разные тела.

Выводы: Гравитационное взаимодействие описывается опытным законом всемирного тяготения. Наиболее часто проявляется в виде силы тяжести и веса тела.

Контрольные вопросы.

2.1. Приведите примеры, когда реализуется состояние невесомости.

Дата добавления: 2014-01-07