Механическая работа

Независимо от характера взаимодействия между частицами изолированной системы векторная сумма импульсов частиц системы остается постоянной.

Контрольные вопросы.

3.1. Может ли сохраняться импульс незамкнутой системы частиц?

3.2. Могут ли тела в замкнутой системе в результате взаимодействия остановиться? Приведите пример такого взаимодействия.

3.3. В чем проявляется сходство и различие соотношений (3.3) и (3.7) со вторым законом Ньютона?

3.4. Существуют ли случаи, когда сумму внешних сил в (3.3) можно считать равнодействующей силой? Если да, то приведите пример.

Понятие механической силы как количественной меры механического взаимодействия объектов не является универсальным. Оно не применимо, вообще говоря, при описании немеханических форм движения. Более общей количественной характеристикой взаимодействия, позволяющей проследить переходы от одних форм движения к другим, является энергия взаимодействия. Как будет показано ниже, количественной мерой изменения механических видов энергии является физическая величина, называемая механической работой, или работой силы.

При действии на материальную точку некоторой силы 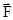, вызывающей элементарное перемещение этой материальной точки 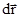, совершается механическая работа, равная скалярному произведению вектора силы 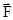на 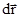, то есть

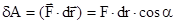. (3.8)

Определению элементарной работы (3.8) можно придать другие формы:

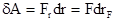. (3.9)

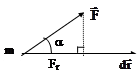
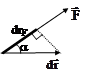
Соотношения (3.8) и (3.9) иллюстрируются рис.3.1, а, б, из

а б

Рис. 3.1

которого очевидны введенные обозначения.

В координатной форме (3.8) имеет вид

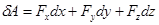. (3.10)

В системе единиц СИ единицей работы является Джоуль (Дж):

1Дж = 1Н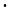1м.

Рассмотрим некоторые свойства механической работы (рис. 3.1).

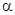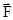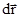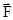1) Если угол между и имеет значения в интервале , то работа силы положительна ().

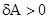2) Если 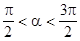, то работа 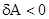- отрицательна.

3) Если 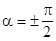, то 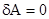. Это тривиальный, но очень важный случай: сила, перпендикулярная перемещению, механической работы не совершает.

Следовательно, составляющая силы 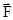, перпендикулярная перемещению 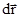, работы не совершает.

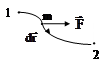
Рис. 3.2

Отметим здесь, что таким свойством обладает магнитная составляющая силы Лоренца (2.17).

4) Механическая работа силы на конечном участке траектории 1-2 (рис. 3.2) равна алгебраической сумме элементарных работ.

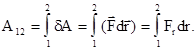(3.11)

Интеграл в (3.11) следует понимать не как обычный определенный интеграл, а как интеграл по траектории движения материальной точки. Это следует из того очевидного факта, что работа произвольной силы, вообще говоря, существенным образом зависит от формы траектории движения материальной точки.

5) Если на материальную точку действуют несколько сил 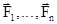, то работа результирующей силы 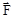равна алгебраической сумме работ каждой из этих сил в отдельности:

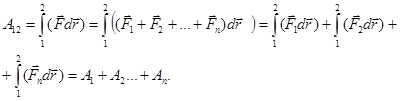
Это свойство непосредственно следует из принципа независимости действия сил.

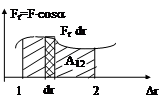
6) Механическая работа имеет простой графический смысл (рис. 3.3):

Рис. 3.3

величина работы численно равна площади криволинейной трапеции, ограниченной графиком проекции силы на перемещение, осью перемещений, начальным и конечным значениями перемещения.

Величина, равная работе силы, совершаемой в единицу времени, называется мощностью, другими словами, мощность характеризует скорость совершения работы. Если за элементарный промежуток времени dt совершается работа 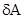, то мощность равна

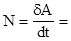
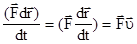. (3.12)

Таким образом, мощность - это величина, равная скалярному произведению вектора силы на вектор скорости материальной точки.

В системе СИ единица мощности называется Ватт (Вт).

1Вт = 1Дж/1с = 1Дж/с.

Вывод: Механической работой называется величина, равная значению криволинейного интеграла от скалярного произведения вектора силы на вектор элементарного перемещения. Интеграл вычисляется вдоль траектории движения точки.

Контрольные вопросы.

3.5. Как вычислить работу постоянной по величине и направлению силы при произвольном виде траектории?

3.6. Чему равна работа силы, вызывающей равномерное вращательное движение материальной точки?

3.4. Кинетическая энергия

Рассмотрим случай, когда на материальную точку действует одна единственная произвольная сила 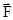.Элементарная работа такой силы согласно (3.8) равна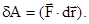

Произведем в этом равенстве замену силы на основании второго закона Ньютона 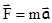: 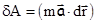и после простых преобразований получим

Легко видеть, что в последнем соотношении произведение 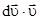можно представить в виде 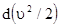. Действительно, при дифференцировании этого выражения имеем

.

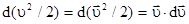Теперь для элементарной работы силы F с учетом постоянства массы материальной точки m получим равенство

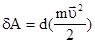. (3.13)

Работа произвольной силы при конечном перемещении материальной точки равна приращению величины :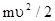

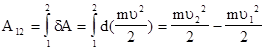. (3.14)

Здесь получен очень важный результат, из которого следует, что работу произвольной силы можно вычислить, не зная ни характера силы, ни вида траектории частицы. Для этого необходима только информация о значениях скорости частицы в начале 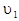и в конце 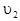рассматриваемого участка движения.

Величина

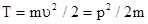(3.15)

называется кинетической энергией материальной точки. В связи с этим на основании равенства (3.14) можно сделать заключение, что механическая работа произвольной силы является количественной мерой приращения кинетической энергии материальной точки, то есть

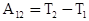. (3.16)

Обсудим некоторые важные свойства кинетической энергии:

1) Непосредственно из (3.15) следует, что кинетическая энергия является функцией механического состояния частицы, так как Т зависит только от ее скорости.

2) Величина Т является аддитивной. Действительно, если на частицы системы действуют различные силы, то работа этих сил равна

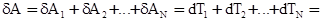
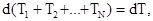
где

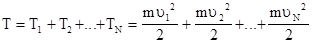
- кинетическая энергия системы частиц. В этом случае работа всех сил, действующих на частицы системы, равна приращению общей кинетической энергии системы материальных точек:

А=.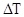

Вывод: Работа произвольных сил в общем случае приводит к изменению кинетической энергии системы.

3.5. Потенциальная энергия и ее связь с силой

Особую роль в механике играют силы, которые называются потенциальными или консервативными силами, и соответствующие им силовые поля.

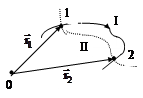
Потенциальной называется сила, работа которой не зависит от формы траектории, а определяется только положением начальной и конечной точек перемещения, то есть работа силы по перемещению материальной точки из положения 1 в положение 2 по пути I (А_{1, I, 2}) равна работе по перемещению по любому другому пути II между теми же положениями (А_1,II,2), то есть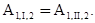

Рис. 3.4

В соответствии с этим определением работа потенциальной силы 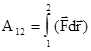должна зависеть только от 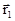и 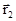- радиус - векторов начального и конечного положений материальной точки в потенциальном силовом поле.

Заметим, что в этом случае интеграл 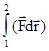из криволинейного становится определенным. Поэтому его значение, а значит и величина работы могут быть представлены с помощью функции 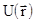, такой, что 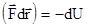, в виде

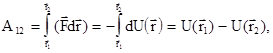(3.17)

где функция положения материальной точки в силовом поле 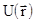называется потенциальной энергией частицы в потенциальном силовом поле. Отметим, что потенциальная энергия частицы - скалярная величина.

Таким образом, работа потенциальной силы является количественной мерой убыли потенциальной энергии частицы в потенциальном силовом поле.

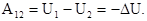(3.18)

Потенциальная энергия обладает следующими свойствами:

1) Потенциальная энергия является функцией состояния материальной точки, так как она зависит только от положения частицы;

2) Величина U является аддитивной, то есть если в области движения частицы имеется несколько потенциальных силовых полей, то полная потенциальная энергия частицы равна сумме потенциальных энергий ее в каждом из полей в отдельности:

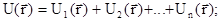
Рис. 3.5

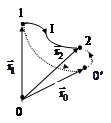
3) Потенциальная энергия частицы определена с точностью до произвольной постоянной величины.

Действительно, из рис. 3.5 видно, что работа при перемещении из положения 1 в положение 2 по пути I равна в соответствии с (3.16)

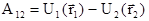. (3.19)

С другой стороны, если из положения 1 в положение 2 частицу перемещать по другой траектории, проходящей через какую - либо точку поля , то

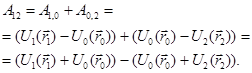(3.20)

Сравнение (3.19) и (3.20) доказывает указанное свойство. Следует отметить, что физически это свойство потенциальной энергии связано с тем фактом, что при перемещении частицы в потенциальном поле работа сил этого поля определяется не самим значением потенциальной энергии, а ее убылью. Это свойство позволяет для однозначности определения потенциальной энергии выбирать ее нулевое значение в произвольной точке силового поля.

Покажем теперь, что между потенциальной энергией частицы и силой, действующей на нее в потенциальном поле, существует определенная универсальная зависимость.

Из (3.17) видно, что элементарная работа в потенциальном поле определяется равенством

которое с учетом (3.10) может быть записано в виде

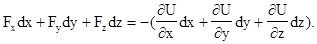
Сравнивая левую и правую части, получим

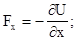
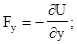
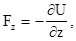(3.21)

или в векторной форме

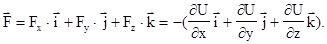(3.22)

Последнее соотношение обычно записывают в одной из символических форм:

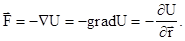(3.23)

В математике вектор с проекциями 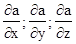называется градиентом скалярной функции 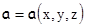, который по модулю равен максимальной скорости возрастания скалярной функции 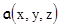и направлен в сторону максимальной скорости возрастания этой функции.

В (3.23) символами 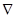(набла), grad (градиент), 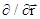обозначен векторный дифференциальный оператор, который в декартовой системе координат имеет вид

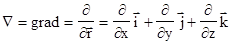(3.24)

и действует на функцию, стоящую справа от него.

Таким образом, равенство (3.23) означает, что сила, действующая на материальную точку в потенциальном поле, равна по величине максимальной скорости возрастания потенциальной энергии в данной точке поля и направлена в сторону наискорейшего убывания потенциальной энергии.

Выводы: Работа по перемещению материальной точки в потенциальном силовом поле не зависит от формы пути и равна убыли потенциальной энергии частицы при данном перемещении.

    Рис. 3.6

Дата добавления: 2014-01-07