Роль закона сохранения механической энергии при решении конкретных задач

Чтобы проиллюстрировать те огромные преимущества, которые дает во многих случаях применение закона сохранения энергии при решении конкретных практических задач, полезно, по мнению автора, рассмотреть решение “очень простой”, на первый взгляд задачи:

Пусть материальная точка m “свободно” вращается в вертикальной плоскости по окружности радиуса R (камень на легкой нерастяжимой веревке). При прохождении верхнего положения скорость частицы 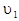. Определить скорость частицы 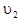при прохождении ею нижнего положения.

Под “свободным” здесь понимается движение частицы под действием двух сил: силы тяжести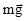и силы натяжения веревки.

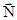а) Попытаемся вначале хотя бы представить ход решения этой задачи на основе применения законов Ньютона (рис.3.11).

Уравнение движения частицы имеет вид

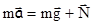
или в проекциях на радиальное и касательное направления:

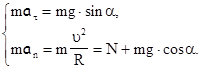
Рис. 3.11

Смысл обозначений ясен из рисунка.

Второе из этих уравнений определяет силу натяжения N и “закон” ее изменения при вращении частицы, поэтому в дальнейшем мы его рассматривать не будем.

Первое уравнение можно преобразовать к одной неизвестной функции времени 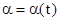с помощью 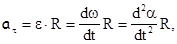после чего получим:

.

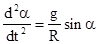К сожалению, несмотря на “простой” вид этого уравнения математически можно решать такое уравнение только приближенно, численными методами. Однако проследить дальнейший ход рассуждений достаточно просто. Предположим, что нам удалось каким-либо методом найти зависимость угла

как функцию времени, то есть 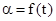.Тогда для момента времени t₂ при прохождении частицей нижнего положения будем иметь

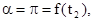
и

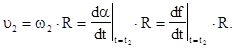
Определив t₂ из первого равенства и подставив во второе, найдем искомое значение скорости ;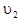

б) Решение этой задачи с помощью закона сохранения механической энергии точно и записывается одной строкой.

Сила тяжести потенциальна, а сила натяжения перпендикулярна скорости частицы, поэтому полная механическая энергия частицы сохраняется. В нижнем положении частицы ее потенциальная энергия в поле силы тяжести принята равной нулю, то есть 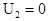. Записав равенство механической энергии для верхнего и нижнего положений

,

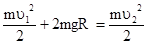имеем значение искомой величины:

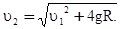
Комментарии излишни.

Дата добавления: 2014-01-07