Сходящиеся последовательности

Определение. Число a называется пределом числовой последовательности { 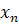}, если 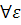>0 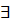N: n>N выполняется неравенство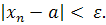

При этом последовательность { 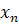} называется сходящейся.

Последовательность не являющаяся сходящейся, называется расходящейся.

Если последовательность { 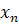} сходится и имеет своим пределом число a, то символически это записывается так 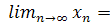a.

Рассмотрим геометрическую интерпретацию определения предела последовательности. Поскольку последовательность представляет собой бесконечное множество чисел, то если она сходится в любой 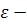окрестности точки a на числовой прямой находится бесконечное число точек элементов этой последовательности, тогда как вне 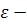окрестности остается конечно число элементов. Поэтому предел последовательности часто называется точкой сгущения.

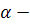
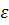
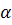
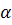
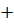
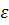
Точка сгущения

Замечание. Неограниченная последовательность не имеет конечного предела. Однако она, может иметь бесконечный предел, что записывается в след. виде .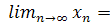

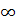Если при этом, начиная с некоторого номера, все члены последовательности положительны (отрицательны), то пишут ( ).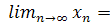

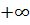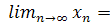
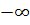Дата добавления: 2014-01-07