Вычисление пределов функций с помощью производной. Правило Лопиталя

В этом параграфе мы рассмотрим удобный прием при вычислении сложных пределов. Будем предполагать в дальнейшем, что 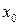либо число, либо один из символов , Предел 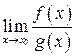называется неопределенностью вида 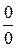(или ), если Раскрыть неопределенность означает найти данный предел.

При раскрытии неопределенносте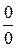й и очень эффективно правило Лопиталя.

Теорема (Лопиталя). Пусть и определены и дифференцируемы в и выполнены условия:

1) и либо обе БМФ, либо обе ББФ при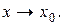

2)

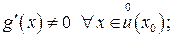
Тогда при условии, что предел справа существует.

Пример 1.

Пример 2.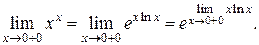

Здесь мы использовали теорему о переходе к пределу под знаком непрерывной функции.

Найдем

Поэтому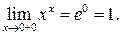

Дата добавления: 2014-01-07