Анализ двух выборок

Вторая часть лекционно-практического материала.

Оглавление

Анализ двух выборок. 2

Использование инструмента Пакет анализа для выявления различий между выборками.. 11

Дисперсионный анализ. 15

Корреляционный анализ. 20

Регрессионный анализ. 28

Выявление достоверности различий. Следующей задачей статистического анализа, решаемой после определения основных выборочных характеристик и анализа одной выборки, является совместный анализ нескольких выборок. Важнейшим вопросом, возникающим при анализе двух выборок, является вопрос о наличии различий между этими выборками. Обычно для этого проводят проверку статистических гипотез о принадлежности обеих выборок одной генеральной совокупности или о равенстве генеральных средних. В рассмотренном ранее примере 6.3. такие различия выявляются путем сравнения данных реализации тур- фирмой путевок за периоды до и после начала активной рекламной компании. Если сопоставить средние значения числа реализованных за месяц путевок до (125,6) и после (145,7) начала рекламной компании, видно, что они различаются. Можно ли по этим данным сделать вывод об эффективности рекламной компании?

Для решения задач такого типа используются так называемые критерии различия. Для проверки одной и той же гипотезы могут быть использованы разные статистические критерии. Правильный выбор критерия определяется как спецификой данных и проверяемых гипотез, так и уровнем статистической подготовки исследователя.

Статистические критерии различия подразделяются на параметрические и непараметрические критерии. Параметрические критерии служат для проверки гипотез о параметрах определенных распределений генеральной совокупности (чаще всего нормального распределения). Непараметрические критерии для проверки гипотез не используют предположений о законе распределения генеральной совокупности и не требуют знания параметров распределения.

Параметрические критерии. Параметрические критерии служат для проверки гипотез о положении и рассеивании. Из параметрических критериев наибольшей популярностью при проверке гипотез о равенстве генеральных средних (математических ожиданий) пользуется е-критерий Стьюдента (е-критерий различия).

Критерий Стьюдента (t) наиболее часто используется для проверки гипотезы: «Средние двух выборок относятся к одной и той же совокупности». Критерий позволяет найти вероятность того, что оба средних относятся к одной и той же совокупности. Если эта вероятность р ниже уровня значимости (р< 0,05), то принято считать, что выборки относятся к двум разным совокупностям.

При использовании t-критерия можно выделить два случая. В первом случае его применяют для проверки гипотезы о равенстве генеральных средних двух независимых, несвязанных выборок (так называемый двухвыборочный t-критерий). В этом случае есть контрольная группа и опытная группа, состоящие, например, из разных пациентов, количество которых в группах может быть различно.

Во втором случае, когда одна и та же группа объектов порождает числовой материал для проверки гипотез о средних, используется так называемый парный -критерий. Выборки при этом называют зависимыми, связанными. Например, измеряется содержание лейкоцитов у здоровых животных, а затем у тех же самых животных после облучения определенной дозой излучения.

В обоих случаях в принципе должно выполняться требование нормальности распределения исследуемого признака в каждой из сравниваемых групп и равенства дисперсий в сравниваемых совокупностях. Однако на практике по большому счету корректное применение t-критерия Стьюдента для двух групп часто бывает затруднительно, поскольку достоверно проверить эти условия удается далеко не всегда.

Для оценки достоверности отличий по критерию Стьюдента принимается нулевая гипотеза, что средние выборок равны между собой. Затем вычисляется значение вероятности того, что изучаемые события (например, количества реализованных путевок в обеих выборках) произошли случайным образом.

В МS Ехсеl для оценки достоверности отличий по критерию Стьюдента используются специальная функция ТТЕСТ и процедуры пакета анализа (см. раздел «Использование Пакета анализа для выявления различий» ниже).

Все перечисленные инструменты вычисляют вероятность, соответствующую критерию Стьюдента, и используются, чтобы определить, насколько вероятно, что две выборки взяты из генеральных совокупностей, которые имеют одно и то же среднее.

Рис. 1 «Главное меню функции ТТЕСТ»

Функция ТТЕСТ использует следующие параметры: ТТЕСТ(массив 1;массив2;хвосты; тип). Здесь:

· массив 1 — это первое множество данных;

· массив2 — это второе множество данных;

· хвосты — число хвостов распределения. Обычно число хвостов равно 2;

· тип — это вид исполняемого е-теста. Возможны З варианта выбора: 1 — парный тест, 2 — двухвыборочный тест с равными дисперсиями, З — двухвыборочный тест с неравными дисперсиями.

Пример 6.8. Выявить, достоверны ли отличия при сравнении данных реализации турфирмой путевок за периоды до и после начала активной рекламной компании

С рекламой	Без рекламы

1. Для проведения статистического анализа прежде всего необходимо ввести данные в рабочую таблицу. Откройте новую рабочую таблицу. Введите в ячейку А1. слово Реклама, затем в ячейки А2:А8 — соответствующие значения числа реализованных путевок. В ячейку В1 введите слова Без рекламы, а в В2:В8 — значения числа реализованных путевок до начала рекламной компании. Отметим, что рассматриваемые группы данных со статистической точки зрения являются выборками

Рис. 2 «Рабочий лист с данными»

2. Для выявления достоверности отличий табличный курсор установите в свободную ячейку (А11). На панели инструментов необходимо нажать кнопку Вставка функции (В появившемся диалоговом окне Мастер функций выберите категорию Статистические и функцию ТТЕСТ, после чего нажмите кнопку ОК. Появившееся диалоговое окно ТТЕСТ за серое поле мышью отодвиньте вправо на 1—2 см от данных (при нажатой левой кнопке). Указателем мыши введите диапазон данных контрольной группы в поле Массив 1 (А2:А8). В поле Массив 2 введите диапазон данных исследуемой группы (В2:В8). В поле Хвосты всегда вводится с клавиатуры цифра 2 (без кавычек), а в поле Тип с клавиатуры введите цифру 3. Нажмите кнопку ОК. В ячейке А11 появится значение вероятности — 0,006295.

3. Поскольку величина вероятности случайного появления анализируемых выборок (0,006295) меньше уровня значимости (α = 0,05), то нулевая гипотеза отвергается. Следовательно, различия между выборками не случайные и средние выборок считаются достоверно отличающимися друг от друга. Поэтому на основании применения критерия Стьюдента можно сделать вывод о большей эффективности реализации путевок после начала рекламной компании (р < 0,05).

Как указывалось выше, при использовании t - критерия выделяют два основных случая. В первом случае его применяют для проверки гипотезы о равенстве генеральных средних двух независимых, несвязанных выборок (так называемый двухвыборочный t-критерий). В этом случае есть две различных выборки, количество элементов в которых может быть также различно. При заполнении диалогового окна ТТЕСТ при этом указывается Тип 3.

Во втором случае, когда одна и та же группа объектов порождает числовой материал для проверки гипотез о средних, используется так называемый парный t-критерий. Выборки при этом называют зависимыми, связанными (при заполнении диалогового окна ТТЕСТ указывается Тип 1). Например, сравнивается реализация путевок двумя фирмами в соответствующие месяцы.

В качестве упражнения рассмотрим пример.

Пример 6.9. Сравнивается количество наличных денег у двух групп студентов (в рублях):

Необходимо определить достоверность различия между группами при двух вариантах постановки задачи:

о группы состоят из различных студентов (тип 3);

о группы состоят из одних и тех же студентов, но первая — до посещения буфета, а вторая — после (тип 1).

Решение. В ячейки С1:С5 введите количество денег у студентов первой группы. В ячейки D1:D5 введите количество денег у студентов второй группы.

1. Табличный курсор установите в свободную ячейку (С6). На панели инструментов необходимо нажать кнопку Вставка функции. В появившемся диалоговом окне Мастер функций выберите категорию Статистические и функцию ТТЕСТ, после чего нажмите кнопку ОК. Появившееся диалоговое окно ТТЕСТ за серое поле мышью отодвиньте вправо на 1—2 см от данных (при нажатой левой кнопке). Указателем мыши ввести диапазон данных первой группы в поле Массив 1 (С1:С5). В поле Массив 2 введите диапазон данных второй группы (D1:D5). В поле Хвосты всегда вводится цифра 2 (без кавычек), а в поле Тип введите цифру 3. Нажмите кнопку ОК. В ячейке С6 появится значение вероятности — 0,228053.

Рис.3 «Функция ТТЕСТ с данными»

Поскольку величина вероятности случайного появлёния анализируемых выборок (0,228053) больше уровня значимости (α = 0,05), то нулевая гипотеза не может быть отвергнута (принимается). Следовательно, различия между выборками могут быть случайными и средние выборок не считаются достоверно отличающимися друг от друга. Поэтому на основании применения критерия Стьюдента нельзя сделать вывод о достоверности отличий двух групп студентов по количеству карманных денег, имеющихся у них (р > 0,05).

2. Табличный курсор установите в свободную ячейку (D6). На панели инструментов нажмите кнопку Вставка функции (f_x). В появившемся диалоговом окне Мастер функций выберите категорию Статистические и функцию ТТЕСТ, после чего нажмите кнопку ОК. Появившееся диалоговое окно ТТЕСТ за серое поле мышью отодвиньте вправо на 1—2 см от данных (при нажатой левой кнопке). Указателем мыши введите диапазон данных первой группы в поле Массив 1 (С1:С5). В поле Массив 2 введите диапазон данных второй группы (D1:D5). В поле Хвосты всегда вводится цифра 2 (без кавычек), а в поле Тип введите цифру 1. Нажмите кнопку ОК. В ячейке D6 появится значение вероятности — 0,003883.

Рис. 4 «Функция ТТЕСТ с данными»

Поскольку величина вероятности случайного появления анализируемых выборок (0,003883) меньше уровня значимости (α = 0,05), то нулевая гипотеза отвергается. Следовательно, различия между выборками не могут быть случайными и средние выборок считаются достоверно отличающимися друг от друга. Поэтому на основании применения критерия Стьюдента можно сделать вывод о том, что в двух группах студентов выявлены достоверные отличия по количеству карманных денег (р < 0,05), что явилось результатом посещения буфета. Таким образом, ясно, что применение различных типов критерия Стьюдента может приводить к различным результатам на основании одних и тех же исходных данных. Можно предложить следующий приблизительный способ выбора типа критерия: если не ясно, какой тип критерия выбирать, выбирается тип 3; если очевидно, что выборки зависимы, связаны (например, это одни и те же студенты), то следует выбирать тип 1.

Критерий Фишера. Критерий Фишера используют для проверки гипотезы о принадлежности двух дисперсий одной генеральной совокупности и, следовательно, их равенстве. При этом предполагается, что данные независимы и распределены по нормальному закону. Гипотеза о равенстве дисперсий принимается, если отношение большей дисперсии к меньшей меньше критического значения распределения Фишера.

где F_крит зависит от уровня значимости и числа степеней свободы для дисперсий в числителе и знаменателе.

В МS Ехсеl для расчета уровня вероятности выполнения гипотезы о равенстве дисперсий могут быть использованы функция ФТЕСТ(массив1;массив2) и процедура пакета анализа Двухвыборочный F-тест для дисперсий.

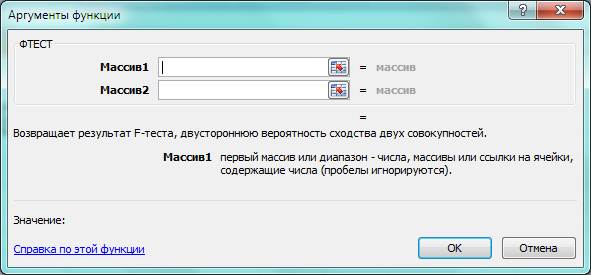
Рис. 5 «Основное меню функции ФТЕСТ»

Непараметрические критерии. Непараметрические критерии используются в тех случаях, когда закон распределения данных отличается от нормального или неизвестен. Из большого числа непараметрических критериев рассмотрим критерий хи - квадрат.

Критерий согласия Х². Бывают ситуации, когда необходимо сравнить две относительные или выраженные в процентах величины (доли). Примером может служить случай проверки успешности трудоустройства молодых специалистов, когда известен процент трудоустроившихся выпускников двух институтов. для проверки достоверности различий здесь критерий Стьюдента применить не удастся. В таких задачах обычно используют критерий х² (хи - квадрат). Критерий хи - квадрат относится к непараметрическим критериям. Здесь, как и в случае с критерием Стьюдента, принимается нулевая гипотеза о том, что выборки принадлежат к одной генеральной совокупности. Кроме того, определяется ожидаемое значение результата. Обычно это среднее значение между выборками рассматриваемого показателя. Затем оценивается вероятность того, что ожидаемые значения и наблюдаемые принадлежат к одной генеральной совокупности.

В МS Ехсеl критерий хи - квадрат реализован в функции ХИ2ТЕСТ. Функция ХИ2ТЕСТ вычисляет вероятность совпадения наблюдаемых (фактических) значений и теоретических (гипотетических) значений. Если вычисленная вероятность ниже уровня значимости (0,05), то нулевая гипотеза отвергается и утверждается, что наблюдаемые значения не соответствуют теоретическим (ожидаемым) значениям.

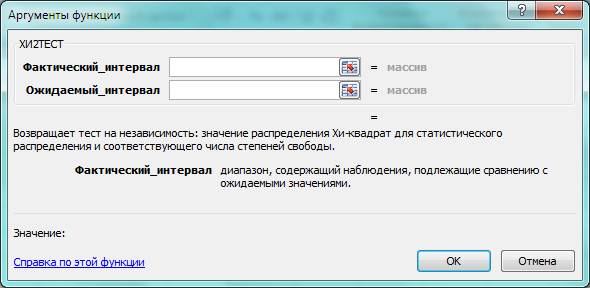
Рис. 6 «Основное меню функции «ХИ2ТЕСТ»»

Функция имеет следующие параметры: ХИ2ТЕСТ(фактический_интервал;ожидае- мый_интервал). Здесь:

· фактический_интервал — это интервал данных, которые содержат наблюдения, подлежащие сравнению с ожидаемыми значениями;

· ожидаемый_интервал — это интервал данных, который содержит теоретические (ожидаемые) значения для соответствующих наблюдаемых.

Пример 6.10. Пусть после окончания двух институтов экономического профиля трудоустроилось по специальности из первого института 90 человек, а из второго 60 (обе группы молодых специалистов включали по 100 человек).

Дата добавления: 2014-01-07